冀教版七年级上册4.4 整式的加减(共17张PPT)
文档属性
| 名称 | 冀教版七年级上册4.4 整式的加减(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 14:24:20 | ||
图片预览






文档简介
(共17张PPT)
第十七章 有理数
4.4 整式的加减
1.合并同类项的法则是什么?
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
(1)括号外的因数是正数,去括号后式子各项的符号与原括号内式子相应各项的符号相同.
(2)括号外的因数是负数,去括号后式子各项的符号与原括号内式子相应各项的符号相反.
2.去括号的法则是什么?
知识回顾
复习
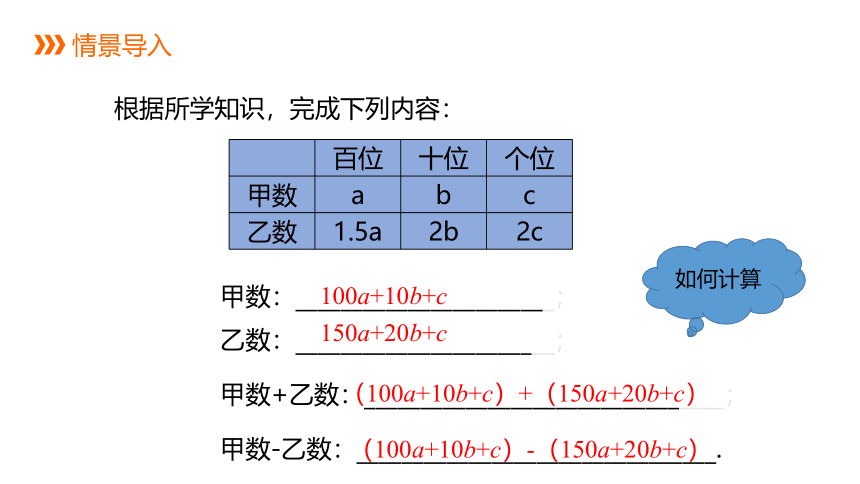
根据所学知识,完成下列内容:
甲数:_______________________;
百位 十位 个位
甲数 a b c
乙数 1.5a 2b 2c
乙数:_______________________;
100a+10b+c
150a+20b+c
甲数+乙数:________________________________;
(100a+10b+c)+(150a+20b+c)
甲数-乙数:________________________________.
(100a+10b+c)-(150a+20b+c)
情景导入
如何计算
七年级(一)班分成三个组,利用星期日参加社会公益活动。第一组有学生m名;第二组的人数比第一组的2倍少10人;第三组的人数是第二组的一半,七年级(一)班一共有学生多少名?
解:七年级(一)班的学生总数是
m+(2m-10)+0.5(2m-10)
=m+2m-10+m-5 (去括号)
=4m-15 (合并同类项)
所以,七年级(一)班共有学生(4m-15)。
获取新知
一起探究
概括
不难发现,去括号和合并同类项是整式加减的基础。因此,整式加减一般步骤可以总结为:
(1) 如果有括号,那么按去括号法则先
去括号。
(2) 如果有同类项,再合并同类项,直到算式中没有同类项为止。
例1 求整式4-5x2+3x与-2x +7x2-3的和.
解:(4-5x2+3x)+(-2x +7x2-3)
=4-5x2+3x-2x +7x2-3
=(-5x2+7x2)+(3x-2x)+(4-3)
=42x2+x+1.
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
例题讲解
例2 先化简,再求值.
,其中x=1,y=-2.
解:
当x=1,y=-2时,
(1)整式的加减运算重点注意去括号时的符号、系数的处理,不要把符号弄错,不要漏乘括号外的系数;
(2)整式的化简求值题,能够化简的最好先化简,尽量不要直接把字母的值代入计算.
方法归纳
例3 一个长方形的宽为a,长比宽的2倍小1.
(1) 写出这个长方形的周长.
(2) 当a=2时,这个长方形的周长是多少?
(3) 当a为何值时,这个长方形的周长是16?
解:(1)这个长方形的周长是2a+2(2a-1)=6a-2.
(2)当a=2时,6a-2=6×2-2=10.
所以这个长方形的周长是10.
(3)如果6a-2=16,那么6a=18,即a=3.
所以,当a=3时,这个长方形的周长是16.
利用整式加减解决实际问题时,先要把具体量用代数式表示出来,然后根据整式加减运算的步骤进行计算.
注意最后结果是几个单项式的和的形式,且要带单位时,要整体加括号.
方法归纳
2.长方形的一边长等于3a+2b,另一边比它大a-b,那么这个长方形的周长是( )
A.14a+6b B.7a+3b C.10a+10b D.12a+8b
1.已知一个多项式与 的和等于 ,则这个多项式是( )
A
A
随堂演练
3.若M-(-3x)=2x2-3x-3,则M应该是( )
A.2x2-3 B.2x2-3x-3
C.2x2-6x-3 D.2x2-6x-3
C
4.若A是一个二次二项式,B是一个五次五项式,则B-A一定是( )
A.二次多项式 B.三次多项式
C.五次三项式 D. 五次多项式
D
5.若A=x2-2xy+y2,B=x2+2xy+y2,则结果为4xy的式子是( )
A.A+B B.B-A C.A-B D.2A-2B
B
6.已知 则
-9a2+5a-4
7.若mn=m+3,则2mn+3m-5mn+10=______.
1
8. 先化简,再求值:
其中a=4.
解:
原式
当a=4时,
原式
9.三角形的周长为48,第一条边的长为3a+2b,第二条边的长比第一条边的长的2倍少a,求第三条边的长.
解:第二条边的长为2(3a+2b)-a=5a+4b,
所以第三条边的长为:
48-(3a+2b)-(5a+4b)=48-8a-6b.
10.多项式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x的取值无关,求a,b的值.
解:(x2+ax-2y+7)-(bx2-2x+9y-1)
=x2+ax-2y+7-bx2+2x-9y+1=(1-b)x2+(a+2)x-11y+8
∵代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x 的取值无关,
∴1-b=0,a+2=0,解得a=-2 ,b=1.
答:a=-2 ,b=1.
整式的加减
整式的加减运算
整式加减的应用
比较复杂的式子求值,先化简,再把数值代入计算.
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项,我们就可以完成整式的加减运算.
列整式解决实际问题:先要把具体量用代数式表示出来,然后根据整式加减运算的步骤进行计算.
课堂小结
第十七章 有理数
4.4 整式的加减
1.合并同类项的法则是什么?
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
(1)括号外的因数是正数,去括号后式子各项的符号与原括号内式子相应各项的符号相同.
(2)括号外的因数是负数,去括号后式子各项的符号与原括号内式子相应各项的符号相反.
2.去括号的法则是什么?
知识回顾
复习
根据所学知识,完成下列内容:
甲数:_______________________;
百位 十位 个位
甲数 a b c
乙数 1.5a 2b 2c
乙数:_______________________;
100a+10b+c
150a+20b+c
甲数+乙数:________________________________;
(100a+10b+c)+(150a+20b+c)
甲数-乙数:________________________________.
(100a+10b+c)-(150a+20b+c)
情景导入
如何计算
七年级(一)班分成三个组,利用星期日参加社会公益活动。第一组有学生m名;第二组的人数比第一组的2倍少10人;第三组的人数是第二组的一半,七年级(一)班一共有学生多少名?
解:七年级(一)班的学生总数是
m+(2m-10)+0.5(2m-10)
=m+2m-10+m-5 (去括号)
=4m-15 (合并同类项)
所以,七年级(一)班共有学生(4m-15)。
获取新知
一起探究
概括
不难发现,去括号和合并同类项是整式加减的基础。因此,整式加减一般步骤可以总结为:
(1) 如果有括号,那么按去括号法则先
去括号。
(2) 如果有同类项,再合并同类项,直到算式中没有同类项为止。
例1 求整式4-5x2+3x与-2x +7x2-3的和.
解:(4-5x2+3x)+(-2x +7x2-3)
=4-5x2+3x-2x +7x2-3
=(-5x2+7x2)+(3x-2x)+(4-3)
=42x2+x+1.
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
例题讲解
例2 先化简,再求值.
,其中x=1,y=-2.
解:
当x=1,y=-2时,
(1)整式的加减运算重点注意去括号时的符号、系数的处理,不要把符号弄错,不要漏乘括号外的系数;
(2)整式的化简求值题,能够化简的最好先化简,尽量不要直接把字母的值代入计算.
方法归纳
例3 一个长方形的宽为a,长比宽的2倍小1.
(1) 写出这个长方形的周长.
(2) 当a=2时,这个长方形的周长是多少?
(3) 当a为何值时,这个长方形的周长是16?
解:(1)这个长方形的周长是2a+2(2a-1)=6a-2.
(2)当a=2时,6a-2=6×2-2=10.
所以这个长方形的周长是10.
(3)如果6a-2=16,那么6a=18,即a=3.
所以,当a=3时,这个长方形的周长是16.
利用整式加减解决实际问题时,先要把具体量用代数式表示出来,然后根据整式加减运算的步骤进行计算.
注意最后结果是几个单项式的和的形式,且要带单位时,要整体加括号.
方法归纳
2.长方形的一边长等于3a+2b,另一边比它大a-b,那么这个长方形的周长是( )
A.14a+6b B.7a+3b C.10a+10b D.12a+8b
1.已知一个多项式与 的和等于 ,则这个多项式是( )
A
A
随堂演练
3.若M-(-3x)=2x2-3x-3,则M应该是( )
A.2x2-3 B.2x2-3x-3
C.2x2-6x-3 D.2x2-6x-3
C
4.若A是一个二次二项式,B是一个五次五项式,则B-A一定是( )
A.二次多项式 B.三次多项式
C.五次三项式 D. 五次多项式
D
5.若A=x2-2xy+y2,B=x2+2xy+y2,则结果为4xy的式子是( )
A.A+B B.B-A C.A-B D.2A-2B
B
6.已知 则
-9a2+5a-4
7.若mn=m+3,则2mn+3m-5mn+10=______.
1
8. 先化简,再求值:
其中a=4.
解:
原式
当a=4时,
原式
9.三角形的周长为48,第一条边的长为3a+2b,第二条边的长比第一条边的长的2倍少a,求第三条边的长.
解:第二条边的长为2(3a+2b)-a=5a+4b,
所以第三条边的长为:
48-(3a+2b)-(5a+4b)=48-8a-6b.
10.多项式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x的取值无关,求a,b的值.
解:(x2+ax-2y+7)-(bx2-2x+9y-1)
=x2+ax-2y+7-bx2+2x-9y+1=(1-b)x2+(a+2)x-11y+8
∵代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x 的取值无关,
∴1-b=0,a+2=0,解得a=-2 ,b=1.
答:a=-2 ,b=1.
整式的加减
整式的加减运算
整式加减的应用
比较复杂的式子求值,先化简,再把数值代入计算.
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项,我们就可以完成整式的加减运算.
列整式解决实际问题:先要把具体量用代数式表示出来,然后根据整式加减运算的步骤进行计算.
课堂小结
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
