冀教版数学七年级上册同步课件:5.2 等式的基本性质(共21张PPT)
文档属性
| 名称 | 冀教版数学七年级上册同步课件:5.2 等式的基本性质(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 957.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 21:36:20 | ||
图片预览




文档简介
(共21张PPT)
第五章 一元一次方程
5.2 等式的基本性质
知识回顾
1. 什么叫做一元一次方程?
方程两边都是整式,只含有一个未知数,并且未知数的指数是一次的方程叫一元一次方程。
2. 下列各式中,哪些是一元一次方程?
(1)7+8=15 (2)x+3=8
(3)3x-1 (4)x=0
(5)2x-y=3x+1 (6)
思考:要让天平平衡应该满足什么条件?
情景导入
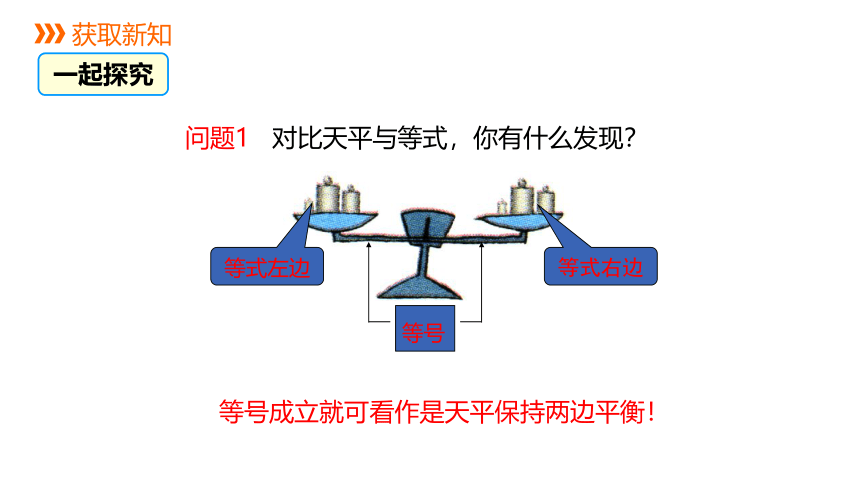
问题1 对比天平与等式,你有什么发现?
等号成立就可看作是天平保持两边平衡!
等式左边
等式右边
等号
获取新知
一起探究
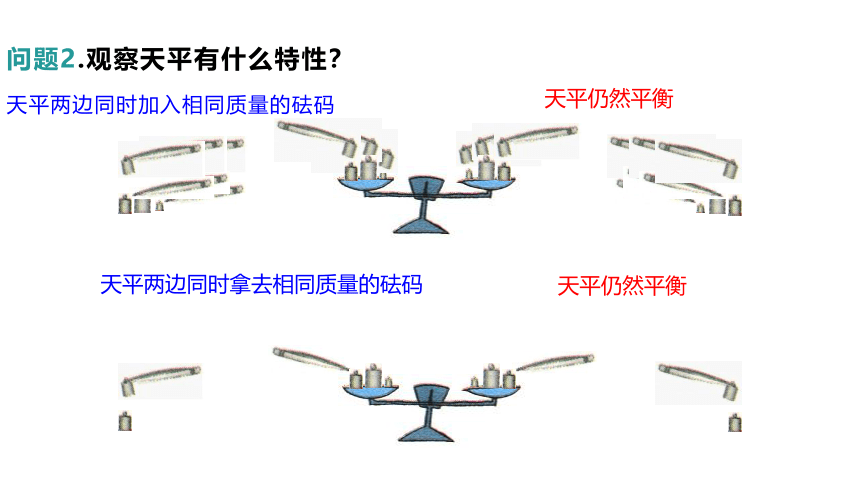
问题2.观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
相同的数 (或式子)
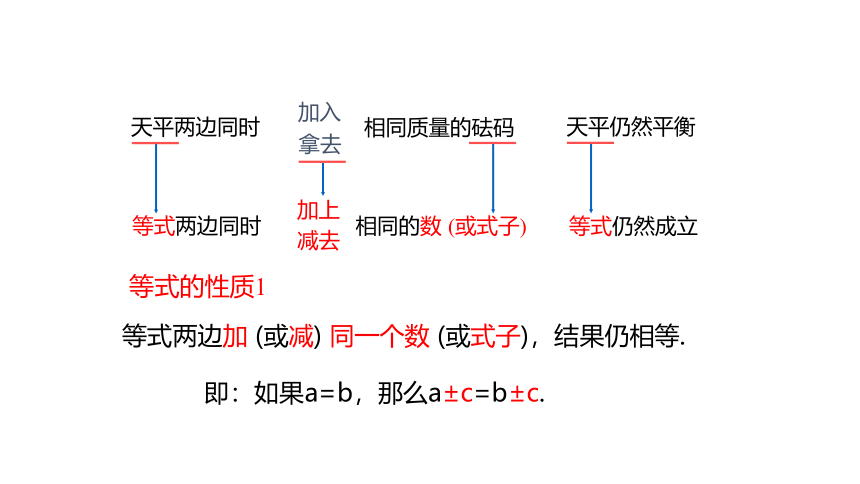
等式两边同时
加上
减去
等式仍然成立
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
即:如果a=b,那么a±c=b±c.
等式的性质1
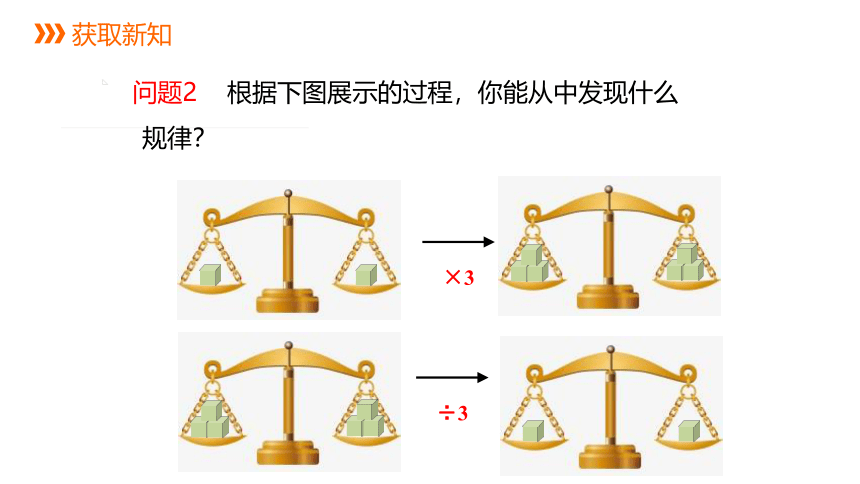
问题2 根据下图展示的过程,你能从中发现什么规律?
×3
÷3
获取新知
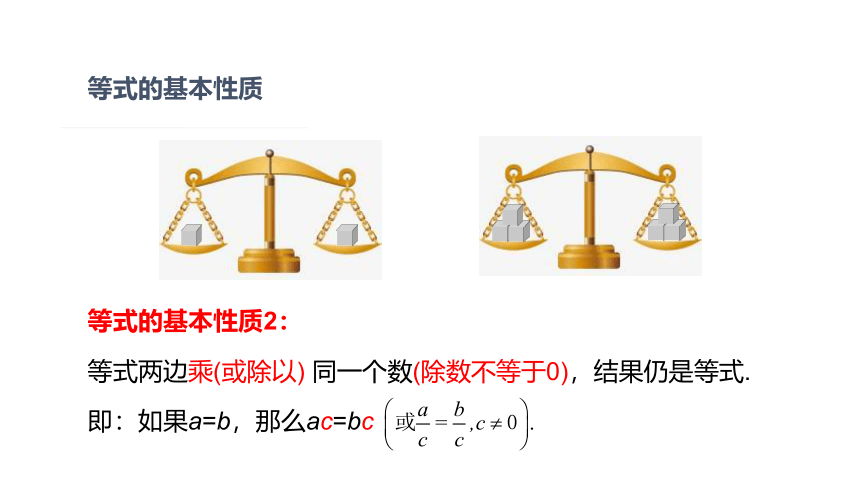
等式的基本性质
等式的基本性质2:
等式两边乘(或除以) 同一个数(除数不等于0),结果仍是等式.
即:如果a=b,那么ac=bc
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b
例题讲解
2x+1=5
2x=4
x=2
两边都减去1
小球的质量x克,一个立方体的质量为1克。
观察探索:
两边都除以2 (或都乘以 )
获取新知
解:两边都减去3,得
x+3-3=8-3
所以
x=8-3,
即
x=5.
例2 解方程:x+3=8.
利用等式的基本性质解方程
等式的基本性质1
获取新知
利用等式的基本性质解方程
x+3=8
x=8-3
两边同时减去3
x+3-3=8-3
化为
将+3改变符号,从左边移到右边
定 义:
在解方程的过程中,将方程中的某一项改变符号后,从等号的一边移到另一边,这种变形过程叫做移项.
⑴ 方程3x-4=1,移项得:3x=1 .
⑵ 方程2x+3=5,移项得:2x= .
⑶ 方程5x=x+1,移项得: .
⑷ 方程2x-7=-5x,移项得: .
⑸ 方程4x=3x-8,移项得: .
⑹ 方程x=3.5x-5x-9,移项得: .
+4
5-3
5x-x=1
2x+5x=7
4x-3x=-8
X-3.5x+5x=-9
注意:移项要改变符号
移项的目的是为了得到形如ax=b的方程(等号的一边是含未知数的项,另一边是常数项)。
例3 解方程 4x-15=9.
解: 移项,得
4x=9+15.
合并同类项,得
4x=24.
两边都除以4,得
x=6.
解:两边都加上15,得
4x-15+15=9+15.
合并同类项,得
4x=24.
两边都除以4,得
x=6.
移项实际上是利用等式的性质 “在方程两边进行同加或同减去同一个数或同一个整式”,但是解题步骤更为简捷!
例题讲解
1.下列等式变形中,错误的是( )
A.由a=b,得a+4=b+4
B.由a=b,得a-3=b-3
C.由x+1=y+1,得x=y
D.由-2x=-2y,得x=-y
D
随堂演练
2.下列方程的变形,符合等式的基本性质的是( )
A.由2x-3=7,得2x=7-3
B.由3x-2=x+1,得3x-x=1-2
C.由-2x=5,得x=5+2
D.由-0.5x=1,得x=-2
D
3.如果ac=ab,那么下列等式中不一定成立的是( )
A.ac-1=ab-1 B.ac+a=ab+a
C.-3ac=-3ab D.c=b
D
4. 填空:
(1) 将等式x-3=5 的两边都_____得到x =8 ,这是根据等式的性质__;
(2) 将等式 的两边都乘以___或除以 ___得到 x = -2,这是根据等式性质 ___;
加3
1
2
2
(3) 将等式x + y =0的两边都_____得到x = -y,这是根据等式的性质___;
(4) 将等式 xy =1的两边都______得到 ,这是根据等 式的性质___.
减y
1
除以x
2
5.(1)如果等式7(x+2)=13(x+2)成立,那么x+2= ,即x= ;
(2)若x-1=2021-y,则x+y= .
2022
0
-2
6.解下列方程.
解:(1)两边都加上3,得 x-3+3=-11+3.
所以 x=-11+3.
即 x=-8.
(2)两边都减去4,得 2x+4-4=10-4.
所以 2x=6.
两边同时除以2,得 2x÷2=6÷2.
即 x=3.
等式的基本性质
利用等式的基本性质1,2
利用等式的基本性质解方程
等式的基本性质1:等式两边加上(或减去) 同一个数或同一个整式,结果仍是等式.
即:如果a=b,那么a±c=b±c.
移项的概念
在解方程的过程中,将方程中的某一项改变符号后,从等号的一边移到另一边,这种变形过程叫做移项.
等式的基本性质2:等式两边乘(或除以) 同一个数(除数不等于0),结果仍是等式.
即:如果a=b,那么ac=bc
课堂小结
第五章 一元一次方程
5.2 等式的基本性质
知识回顾
1. 什么叫做一元一次方程?
方程两边都是整式,只含有一个未知数,并且未知数的指数是一次的方程叫一元一次方程。
2. 下列各式中,哪些是一元一次方程?
(1)7+8=15 (2)x+3=8
(3)3x-1 (4)x=0
(5)2x-y=3x+1 (6)
思考:要让天平平衡应该满足什么条件?
情景导入
问题1 对比天平与等式,你有什么发现?
等号成立就可看作是天平保持两边平衡!
等式左边
等式右边
等号
获取新知
一起探究
问题2.观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
相同的数 (或式子)
等式两边同时
加上
减去
等式仍然成立
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
即:如果a=b,那么a±c=b±c.
等式的性质1
问题2 根据下图展示的过程,你能从中发现什么规律?
×3
÷3
获取新知
等式的基本性质
等式的基本性质2:
等式两边乘(或除以) 同一个数(除数不等于0),结果仍是等式.
即:如果a=b,那么ac=bc
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b
例题讲解
2x+1=5
2x=4
x=2
两边都减去1
小球的质量x克,一个立方体的质量为1克。
观察探索:
两边都除以2 (或都乘以 )
获取新知
解:两边都减去3,得
x+3-3=8-3
所以
x=8-3,
即
x=5.
例2 解方程:x+3=8.
利用等式的基本性质解方程
等式的基本性质1
获取新知
利用等式的基本性质解方程
x+3=8
x=8-3
两边同时减去3
x+3-3=8-3
化为
将+3改变符号,从左边移到右边
定 义:
在解方程的过程中,将方程中的某一项改变符号后,从等号的一边移到另一边,这种变形过程叫做移项.
⑴ 方程3x-4=1,移项得:3x=1 .
⑵ 方程2x+3=5,移项得:2x= .
⑶ 方程5x=x+1,移项得: .
⑷ 方程2x-7=-5x,移项得: .
⑸ 方程4x=3x-8,移项得: .
⑹ 方程x=3.5x-5x-9,移项得: .
+4
5-3
5x-x=1
2x+5x=7
4x-3x=-8
X-3.5x+5x=-9
注意:移项要改变符号
移项的目的是为了得到形如ax=b的方程(等号的一边是含未知数的项,另一边是常数项)。
例3 解方程 4x-15=9.
解: 移项,得
4x=9+15.
合并同类项,得
4x=24.
两边都除以4,得
x=6.
解:两边都加上15,得
4x-15+15=9+15.
合并同类项,得
4x=24.
两边都除以4,得
x=6.
移项实际上是利用等式的性质 “在方程两边进行同加或同减去同一个数或同一个整式”,但是解题步骤更为简捷!
例题讲解
1.下列等式变形中,错误的是( )
A.由a=b,得a+4=b+4
B.由a=b,得a-3=b-3
C.由x+1=y+1,得x=y
D.由-2x=-2y,得x=-y
D
随堂演练
2.下列方程的变形,符合等式的基本性质的是( )
A.由2x-3=7,得2x=7-3
B.由3x-2=x+1,得3x-x=1-2
C.由-2x=5,得x=5+2
D.由-0.5x=1,得x=-2
D
3.如果ac=ab,那么下列等式中不一定成立的是( )
A.ac-1=ab-1 B.ac+a=ab+a
C.-3ac=-3ab D.c=b
D
4. 填空:
(1) 将等式x-3=5 的两边都_____得到x =8 ,这是根据等式的性质__;
(2) 将等式 的两边都乘以___或除以 ___得到 x = -2,这是根据等式性质 ___;
加3
1
2
2
(3) 将等式x + y =0的两边都_____得到x = -y,这是根据等式的性质___;
(4) 将等式 xy =1的两边都______得到 ,这是根据等 式的性质___.
减y
1
除以x
2
5.(1)如果等式7(x+2)=13(x+2)成立,那么x+2= ,即x= ;
(2)若x-1=2021-y,则x+y= .
2022
0
-2
6.解下列方程.
解:(1)两边都加上3,得 x-3+3=-11+3.
所以 x=-11+3.
即 x=-8.
(2)两边都减去4,得 2x+4-4=10-4.
所以 2x=6.
两边同时除以2,得 2x÷2=6÷2.
即 x=3.
等式的基本性质
利用等式的基本性质1,2
利用等式的基本性质解方程
等式的基本性质1:等式两边加上(或减去) 同一个数或同一个整式,结果仍是等式.
即:如果a=b,那么a±c=b±c.
移项的概念
在解方程的过程中,将方程中的某一项改变符号后,从等号的一边移到另一边,这种变形过程叫做移项.
等式的基本性质2:等式两边乘(或除以) 同一个数(除数不等于0),结果仍是等式.
即:如果a=b,那么ac=bc
课堂小结
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
