冀教版数学七年级上册5.4 第5课时 几何图形及动点问题 同步课件(共22张PPT)
文档属性
| 名称 | 冀教版数学七年级上册5.4 第5课时 几何图形及动点问题 同步课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 07:01:07 | ||
图片预览





文档简介
(共22张PPT)
第五章 一元一次方程
5.4 第5课时 几何问题
试一试:
你能用列方程解决下列问题吗?
(1)已知∠A的余角的补角是101°,求∠A的度数;
(2)已知一个三角形三个内角的度数比为2:3:4,求三个内角的度数.
解:(1)设∠A的度数为x.依题意,得
180°-( 90°-x)= 101°.
解得 x=11°.
(2)设三个内角的度数分别是2 x 、3 x 、4 x.依题意,得 2 x +3 x +4 x = 180°.
解得 x=20°.
所以三个内角的度数分别为40°,60°,80°.
情景导入
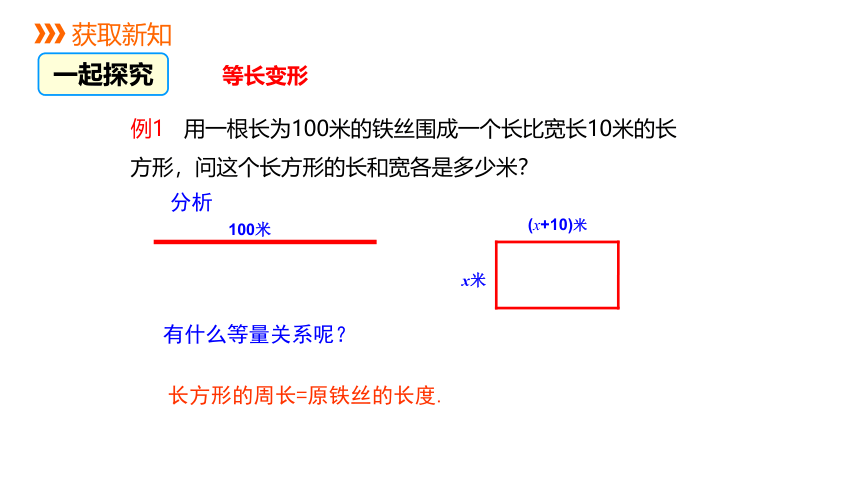
例1 用一根长为100米的铁丝围成一个长比宽长10米的长方形,问这个长方形的长和宽各是多少米?
等长变形
100米
x米
有什么等量关系呢?
长方形的周长=原铁丝的长度.
(x+10)米
分析
获取新知
一起探究
解:设长方形的宽x米,则长为(x+10)米. 根据题意,得
2(x+x+10)=100
所以长为:x+10=20+10=30米
答:该长方形的长为30米,宽为20米.
解得 x =20
几何图形问题
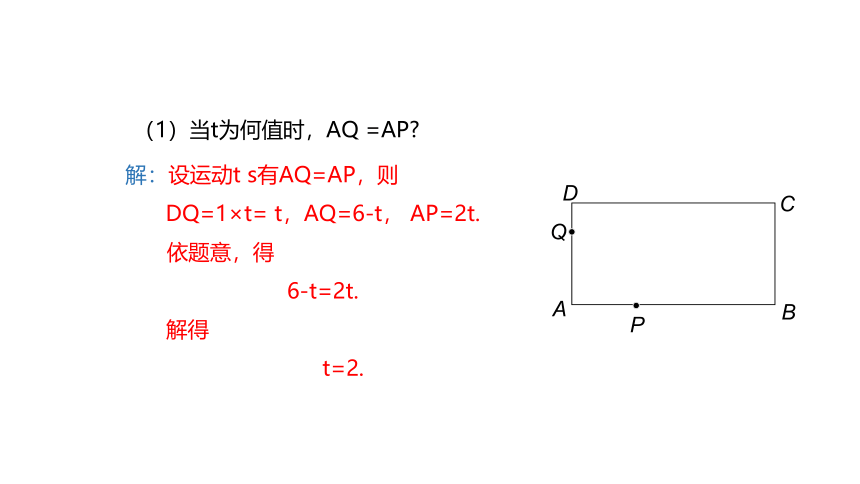
例2 如图,在长方形ABCD中,AB=12 cm,BC=6 cm.动点P沿AB边从点A开始,向点B以2 cm/s的速度运动;动点Q沿DA边从点D开始,向点A以1 cm/s的速度运动.P,Q同时开始运动,用t (s)表示移动的时间.
(1)当t为何值时,AQ =AP
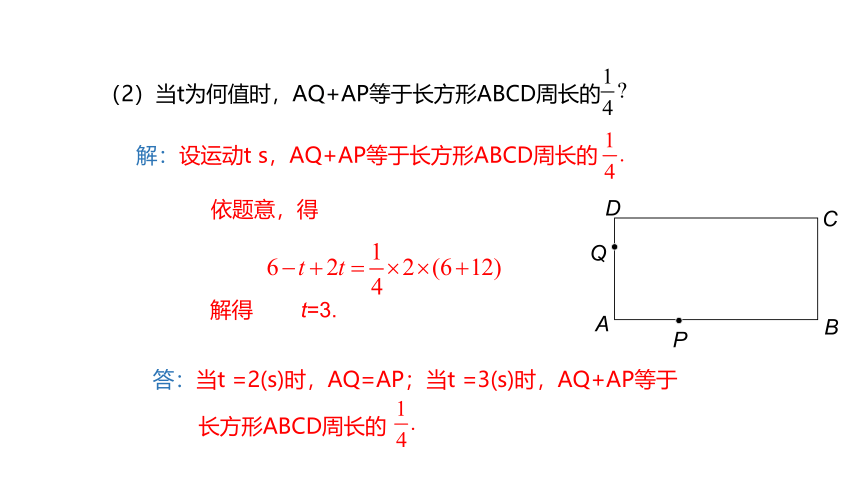
(2)当t为何值时,AQ+AP等于长方形ABCD周长的
D
A
B
C
Q
P
获取新知
一起探究
解:设运动t s有AQ=AP,则
DQ=1×t= t,AQ=6-t, AP=2t.
依题意,得
6-t=2t.
解得
t=2.
(1)当t为何值时,AQ =AP
D
A
B
C
Q
P
依题意,得
解得 t=3.
D
A
B
C
Q
P
(2)当t为何值时,AQ+AP等于长方形ABCD周长的
解:设运动t s,AQ+AP等于长方形ABCD周长的
答:当t =2(s)时,AQ=AP;当t =3(s)时,AQ+AP等于
长方形ABCD周长的
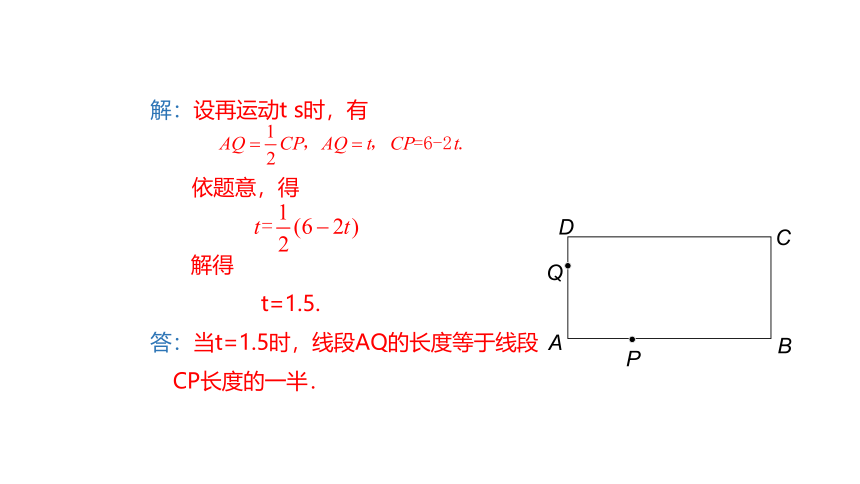
问题 在例1的情境中,如果点P到达点B后沿BC方向继续运动,点Q到达点A后沿AB方向继续运动,如图所示.当点P到达点C时,点P和点Q同时停止运动.试求当t为何值时,线段AQ的长度等于线段CP长度的一半.
D
A
B
C
P
Q
解:设再运动t s时,有
依题意,得
解得
t=1.5.
答:当t=1.5时,线段AQ的长度等于线段
CP长度的一半.
D
A
B
C
Q
P
归 纳:
将几何图形赋予了代数元素,便产生了一类新问题,解决这类问题时,通常要用到图形的性质以及几何量之间的关系.
几何图形问题
例3 已知:如图数轴上两动点A、B原始位置所对应的数分别为﹣3、1,
(1)若点P是线段AB的中点,点P对应的数记为a,请直接写出a的值;
获取新知
一起探究
数轴上的动点问题
解:(1)a的值:(﹣3+1)÷2=﹣1.
故a的值是﹣1;
(2)若点A以每秒钟4个单位向右运动,同时点B以每秒钟2个单位长度也向右运动,求点A和点B相遇时的位置所表示的数b的值;
(2)设经过x秒点A和点B相遇,依题意有
4x﹣2x=1﹣(﹣3),
解得x=2,
1+2×2=5.
故数b的值为5;
(3)当另一动点Q以每秒钟1个单位长度的速度从原点O向右运动时,同时点A以每秒钟4个单位长度向右运动,点B以每秒钟2个单位长度向右运动,问几秒钟后QA=2QB?
解:(3)设经过y秒后QA=2QB.
∴|y﹣(4y﹣3)|=2(2y+1﹣y),
解得y=5或 ,
故5或 秒钟后QA=2QB.
随堂演练
1.一个宽为3cm的长方形与一个边长为6cm的正方形面积相等,则这个长方形的周长为 ( )
A.12cm B.18cm C.24cm D.30cm
D
2.某中学准备建一个面积为375 m2的矩形游泳
池,且游泳池的宽比长短10 m,设游泳池的长
为x m,则可列方程为( )
A.x(x-10)=375 B. x(x+10)=375
C. 2x(2x-10)=375 D. 2x(2x+10)=375
A
3.长方形的长和宽如图所示,当长方形周长为12时,求a的值.
解:依题意得2(3a﹣1+a+3)=12
即:8a+4=12
解得:a=1
答:a的值是1.
4.已知一个角的补角是这个角的余角的3倍,求这
个角.
解:设这个角为x,则它的余角为(90°-x),
补角为(180°-x)
由题意得180°-x=3(90°-x)
解得x=45°
答:这个角的大小为45°.
5.如图,在三角形ABC中,∠C=90°,AC=6 cm,BC=10 cm,点P从点C开始向点B运动,运动速度是1 cm/s,设运动时间是t s(0<t<10).
(1)用含t的代数式表示三角形ABP的面积;
解:(1)点P运动t s后,CP=t cm,
所以PB=(10-t)cm,
所以三角形ABP的面积
=BP·AC=(30-3t)cm2.
(2)当三角形ABP的面积是三角形ABC的面积的一半时,求t的值,并指出此时点P在BC边上的什么位置.
解:(2)三角形ABC的面积=BC·AC=30(cm2).
依题意,得30-3t=×30,
解得t=5,则CP=5 cm,
即此时P是BC边的中点.
6.如图,已知A,B,C是数轴上的三点,点C表示的数为7,BC=4,AB=16,动点P,Q分别从点A,C同时出发,点P以每秒5个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且CQ=3CN.设运动的时间为t(t>0)秒.
(1)点A表示的数为________,点B表示的数为________;
解:(1)结合题干中的图,因为点C表示的数为7,BC=4,所以点B表示的数为3.
因为AB=16,所以点A表示的数为-13.
(2)当t<6时,求MN的长(用含t的式子表示);
解:(2)由题意得AP=5t,CQ=2t,如图所示:
因为M为AP的中点,所以AM=AP=t,
所以在数轴上点M表示的数是-13+t.
因为点N在CQ上,CQ=3CN,所以CN=t,
所以在数轴上点N表示的数是7-t,
所以MN=7-t-(-13+t)=20-t.
(3)当t为何值时,原点O恰好为线段PQ的中点?
解:(3)由题意,得AP=5t,CQ=2t,分两种情况:
①当点P在原点的左侧,点Q在原点的右侧时,OP=13-5t,OQ=7-2t.
因为O为PQ的中点,所以OP=OQ,所以13-5t=7-2t,
解得t=2,即当t=2时,O为PQ的中点;
②当点P在原点的右侧,点Q在原点的左侧时,OP=5t-13,OQ=2t-7.
因为O为PQ的中点,所以OP=OQ,
所以5t-13=2t-7,解得t=2,
此时AP=10<13,所以t=2不合题意,舍去.
综上所述,当t=2时,原点O恰好为线段PQ的中点.
第五章 一元一次方程
5.4 第5课时 几何问题
试一试:
你能用列方程解决下列问题吗?
(1)已知∠A的余角的补角是101°,求∠A的度数;
(2)已知一个三角形三个内角的度数比为2:3:4,求三个内角的度数.
解:(1)设∠A的度数为x.依题意,得
180°-( 90°-x)= 101°.
解得 x=11°.
(2)设三个内角的度数分别是2 x 、3 x 、4 x.依题意,得 2 x +3 x +4 x = 180°.
解得 x=20°.
所以三个内角的度数分别为40°,60°,80°.
情景导入
例1 用一根长为100米的铁丝围成一个长比宽长10米的长方形,问这个长方形的长和宽各是多少米?
等长变形
100米
x米
有什么等量关系呢?
长方形的周长=原铁丝的长度.
(x+10)米
分析
获取新知
一起探究
解:设长方形的宽x米,则长为(x+10)米. 根据题意,得
2(x+x+10)=100
所以长为:x+10=20+10=30米
答:该长方形的长为30米,宽为20米.
解得 x =20
几何图形问题
例2 如图,在长方形ABCD中,AB=12 cm,BC=6 cm.动点P沿AB边从点A开始,向点B以2 cm/s的速度运动;动点Q沿DA边从点D开始,向点A以1 cm/s的速度运动.P,Q同时开始运动,用t (s)表示移动的时间.
(1)当t为何值时,AQ =AP
(2)当t为何值时,AQ+AP等于长方形ABCD周长的
D
A
B
C
Q
P
获取新知
一起探究
解:设运动t s有AQ=AP,则
DQ=1×t= t,AQ=6-t, AP=2t.
依题意,得
6-t=2t.
解得
t=2.
(1)当t为何值时,AQ =AP
D
A
B
C
Q
P
依题意,得
解得 t=3.
D
A
B
C
Q
P
(2)当t为何值时,AQ+AP等于长方形ABCD周长的
解:设运动t s,AQ+AP等于长方形ABCD周长的
答:当t =2(s)时,AQ=AP;当t =3(s)时,AQ+AP等于
长方形ABCD周长的
问题 在例1的情境中,如果点P到达点B后沿BC方向继续运动,点Q到达点A后沿AB方向继续运动,如图所示.当点P到达点C时,点P和点Q同时停止运动.试求当t为何值时,线段AQ的长度等于线段CP长度的一半.
D
A
B
C
P
Q
解:设再运动t s时,有
依题意,得
解得
t=1.5.
答:当t=1.5时,线段AQ的长度等于线段
CP长度的一半.
D
A
B
C
Q
P
归 纳:
将几何图形赋予了代数元素,便产生了一类新问题,解决这类问题时,通常要用到图形的性质以及几何量之间的关系.
几何图形问题
例3 已知:如图数轴上两动点A、B原始位置所对应的数分别为﹣3、1,
(1)若点P是线段AB的中点,点P对应的数记为a,请直接写出a的值;
获取新知
一起探究
数轴上的动点问题
解:(1)a的值:(﹣3+1)÷2=﹣1.
故a的值是﹣1;
(2)若点A以每秒钟4个单位向右运动,同时点B以每秒钟2个单位长度也向右运动,求点A和点B相遇时的位置所表示的数b的值;
(2)设经过x秒点A和点B相遇,依题意有
4x﹣2x=1﹣(﹣3),
解得x=2,
1+2×2=5.
故数b的值为5;
(3)当另一动点Q以每秒钟1个单位长度的速度从原点O向右运动时,同时点A以每秒钟4个单位长度向右运动,点B以每秒钟2个单位长度向右运动,问几秒钟后QA=2QB?
解:(3)设经过y秒后QA=2QB.
∴|y﹣(4y﹣3)|=2(2y+1﹣y),
解得y=5或 ,
故5或 秒钟后QA=2QB.
随堂演练
1.一个宽为3cm的长方形与一个边长为6cm的正方形面积相等,则这个长方形的周长为 ( )
A.12cm B.18cm C.24cm D.30cm
D
2.某中学准备建一个面积为375 m2的矩形游泳
池,且游泳池的宽比长短10 m,设游泳池的长
为x m,则可列方程为( )
A.x(x-10)=375 B. x(x+10)=375
C. 2x(2x-10)=375 D. 2x(2x+10)=375
A
3.长方形的长和宽如图所示,当长方形周长为12时,求a的值.
解:依题意得2(3a﹣1+a+3)=12
即:8a+4=12
解得:a=1
答:a的值是1.
4.已知一个角的补角是这个角的余角的3倍,求这
个角.
解:设这个角为x,则它的余角为(90°-x),
补角为(180°-x)
由题意得180°-x=3(90°-x)
解得x=45°
答:这个角的大小为45°.
5.如图,在三角形ABC中,∠C=90°,AC=6 cm,BC=10 cm,点P从点C开始向点B运动,运动速度是1 cm/s,设运动时间是t s(0<t<10).
(1)用含t的代数式表示三角形ABP的面积;
解:(1)点P运动t s后,CP=t cm,
所以PB=(10-t)cm,
所以三角形ABP的面积
=BP·AC=(30-3t)cm2.
(2)当三角形ABP的面积是三角形ABC的面积的一半时,求t的值,并指出此时点P在BC边上的什么位置.
解:(2)三角形ABC的面积=BC·AC=30(cm2).
依题意,得30-3t=×30,
解得t=5,则CP=5 cm,
即此时P是BC边的中点.
6.如图,已知A,B,C是数轴上的三点,点C表示的数为7,BC=4,AB=16,动点P,Q分别从点A,C同时出发,点P以每秒5个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且CQ=3CN.设运动的时间为t(t>0)秒.
(1)点A表示的数为________,点B表示的数为________;
解:(1)结合题干中的图,因为点C表示的数为7,BC=4,所以点B表示的数为3.
因为AB=16,所以点A表示的数为-13.
(2)当t<6时,求MN的长(用含t的式子表示);
解:(2)由题意得AP=5t,CQ=2t,如图所示:
因为M为AP的中点,所以AM=AP=t,
所以在数轴上点M表示的数是-13+t.
因为点N在CQ上,CQ=3CN,所以CN=t,
所以在数轴上点N表示的数是7-t,
所以MN=7-t-(-13+t)=20-t.
(3)当t为何值时,原点O恰好为线段PQ的中点?
解:(3)由题意,得AP=5t,CQ=2t,分两种情况:
①当点P在原点的左侧,点Q在原点的右侧时,OP=13-5t,OQ=7-2t.
因为O为PQ的中点,所以OP=OQ,所以13-5t=7-2t,
解得t=2,即当t=2时,O为PQ的中点;
②当点P在原点的右侧,点Q在原点的左侧时,OP=5t-13,OQ=2t-7.
因为O为PQ的中点,所以OP=OQ,
所以5t-13=2t-7,解得t=2,
此时AP=10<13,所以t=2不合题意,舍去.
综上所述,当t=2时,原点O恰好为线段PQ的中点.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
