北师大版八年级数学下册 5.2 探索轴对称的性质 学案(无答案)
文档属性
| 名称 | 北师大版八年级数学下册 5.2 探索轴对称的性质 学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 654.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 00:00:00 | ||
图片预览


文档简介
轴对称的性质
学习目标:
1.在直观认识和操作的基础上,学会用自己的语言表达轴对称性质探索的过程,理解轴对称的性质.
2.会用轴对称的性质解决简单的问题,并能利用性质进行简单作图.
课前准备建议:矩形纸.
第一环节:激活思维
画出下列轴对称图形的所有对称轴,并写出各图形中对称轴的条数.
第二环节:探究新知
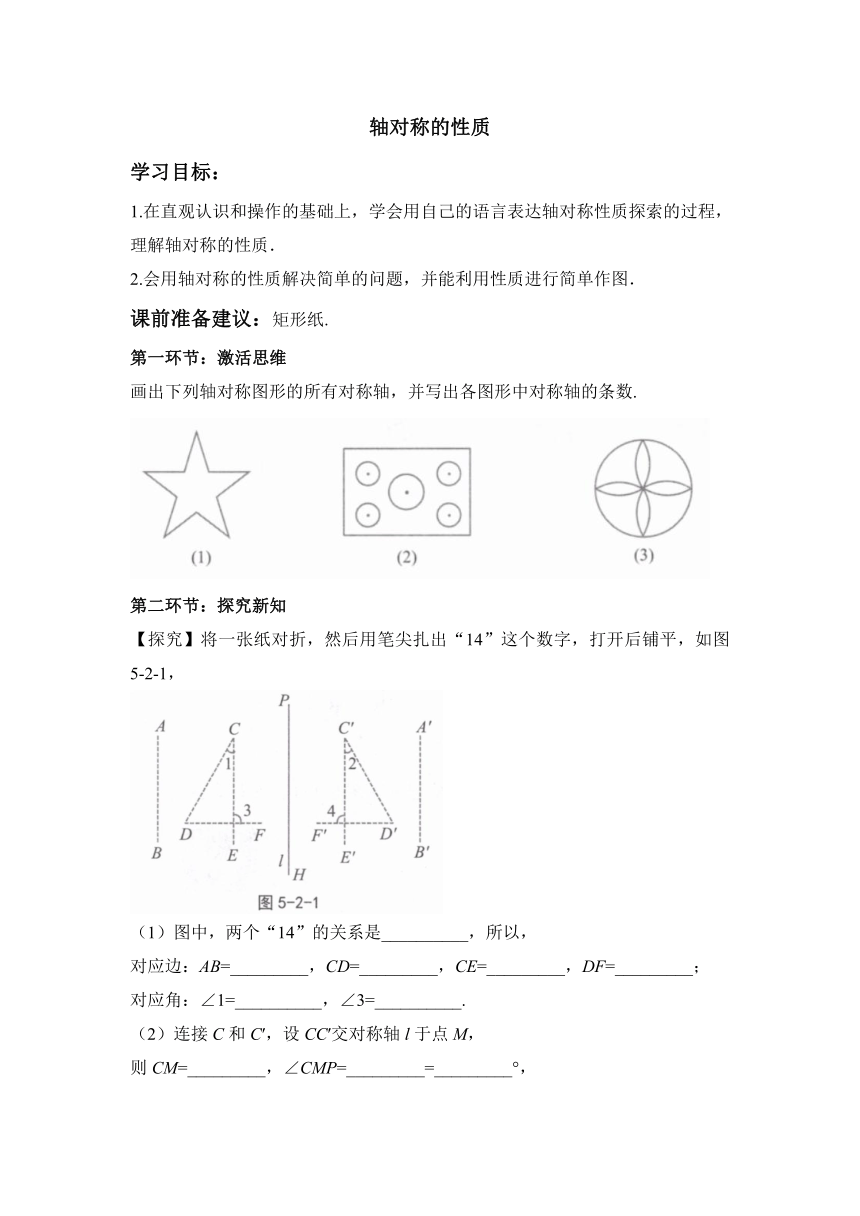
【探究】将一张纸对折,然后用笔尖扎出“14”这个数字,打开后铺平,如图5-2-1,
(1)图中,两个“14”的关系是__________,所以,
对应边:AB=_________,CD=_________,CE=_________,DF=_________;
对应角:∠1=__________,∠3=__________.
(2)连接C和C′,设CC′交对称轴l于点M,
则CM=_________,∠CMP=_________=_________°,
所以直线l是CC′的_________线.
(3)连接BB′,则直线l是BB′的_________线.
轴对称的性质:(1)对应点连线段被对称轴_________.
(2)对应线段_________,对应角_________.
第三环节:双基巩固
【例题1】如图5-2-2是一个轴对称图形:
(1)你能找出它的对称轴吗?
(2)连接点A与点A′的线段与对称轴有什么关系?连接点B与点B′的线段呢?
第四环节:综合运用
【例题2】(1)画出点A关于直线l对称点A′.
(2)画出线段AB关于直线l的轴对称图形.
第五环节:分层反馈
1.如图5-2-3,已知△ABC和直线l,画出△ABC以直线l为对称轴的对称图形.
2.如图5-2-4,镜子中号码的实际号码是__________.
3.如图5-2-5-①是四边形纸片ABCD,其中∠B=120°,∠D=50°,若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图②所示,则∠C=( )
A.80° B.85° C.95° D.110°
4.如图5-2-6,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24cm,△ECF的周长为8cm,四边形纸片ABCD的周长为__________.
5.(★)如图5-2-7,某乡为了解决所辖范围内张家村A和李家村B的饮水问题,决定在河MN边打开一个缺口P将河水引入到张家村A和李家村B.为了节约资金,使修建的水渠最短,应将缺口P修建在哪里?
学习目标:
1.在直观认识和操作的基础上,学会用自己的语言表达轴对称性质探索的过程,理解轴对称的性质.
2.会用轴对称的性质解决简单的问题,并能利用性质进行简单作图.
课前准备建议:矩形纸.
第一环节:激活思维
画出下列轴对称图形的所有对称轴,并写出各图形中对称轴的条数.
第二环节:探究新知
【探究】将一张纸对折,然后用笔尖扎出“14”这个数字,打开后铺平,如图5-2-1,
(1)图中,两个“14”的关系是__________,所以,
对应边:AB=_________,CD=_________,CE=_________,DF=_________;
对应角:∠1=__________,∠3=__________.
(2)连接C和C′,设CC′交对称轴l于点M,
则CM=_________,∠CMP=_________=_________°,
所以直线l是CC′的_________线.
(3)连接BB′,则直线l是BB′的_________线.
轴对称的性质:(1)对应点连线段被对称轴_________.
(2)对应线段_________,对应角_________.
第三环节:双基巩固
【例题1】如图5-2-2是一个轴对称图形:
(1)你能找出它的对称轴吗?
(2)连接点A与点A′的线段与对称轴有什么关系?连接点B与点B′的线段呢?
第四环节:综合运用
【例题2】(1)画出点A关于直线l对称点A′.
(2)画出线段AB关于直线l的轴对称图形.
第五环节:分层反馈
1.如图5-2-3,已知△ABC和直线l,画出△ABC以直线l为对称轴的对称图形.
2.如图5-2-4,镜子中号码的实际号码是__________.
3.如图5-2-5-①是四边形纸片ABCD,其中∠B=120°,∠D=50°,若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图②所示,则∠C=( )
A.80° B.85° C.95° D.110°
4.如图5-2-6,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24cm,△ECF的周长为8cm,四边形纸片ABCD的周长为__________.
5.(★)如图5-2-7,某乡为了解决所辖范围内张家村A和李家村B的饮水问题,决定在河MN边打开一个缺口P将河水引入到张家村A和李家村B.为了节约资金,使修建的水渠最短,应将缺口P修建在哪里?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
