青岛版九年级数学下册 6.5事件的概率 教学课件(共18张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 6.5事件的概率 教学课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 09:33:54 | ||
图片预览





文档简介
(共18张PPT)
第6章 事件的概率
6.5 事件的概率(2)
Contents
目录
01
02
03
04
学习目标
新课导入
当堂检测
课堂小结
典例探究
跟踪练习
05
06
1.了解随机事件发生的不确定性和概率的稳定性;
2.正确理解概率的含义,理解频率与概率的区别与联系;
3.利用概率解决生活中的实际问题.
频率与概率的关系
随着试验次数的增加, 频率会在概率的附近摆动,并趋于稳定.在实际问题中,若事件的概率未知,常用频率作为它的估计值.
频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同.而概率是一个确定数,是客观存在的,与每次试验无关.
(1)联系:
(2)区别:
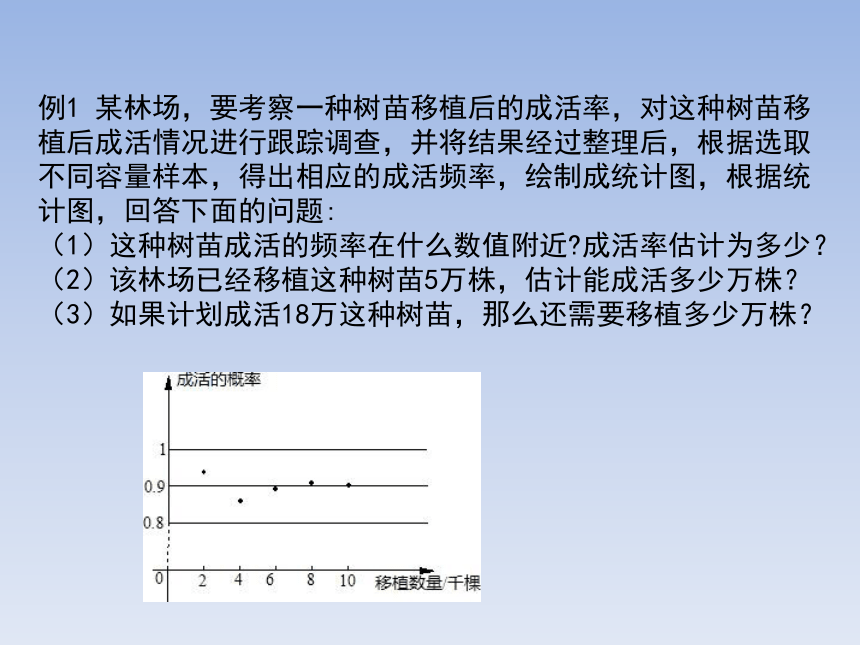
例1 某林场,要考察一种树苗移植后的成活率,对这种树苗移植后成活情况进行跟踪调查,并将结果经过整理后,根据选取不同容量样本,得出相应的成活频率,绘制成统计图,根据统计图,回答下面的问题:
(1)这种树苗成活的频率在什么数值附近 成活率估计为多少?
(2)该林场已经移植这种树苗5万株,估计能成活多少万株?
(3)如果计划成活18万这种树苗,那么还需要移植多少万株?
分析:(1)由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9; (2)5×成活率即为所求的成活的树苗棵树; (3)利用成活率求得需要树苗棵数,减去已移植树苗数即为所求的树苗的棵数.
解:(1)这种树苗成活的频率稳定在0.9,
成活的概率估计值为0.9. (2)估计这种树苗成活在5×0.9=4.5万棵; (3)18÷0.9-5=15, 答:该地区还需移植这种树苗约15万棵.
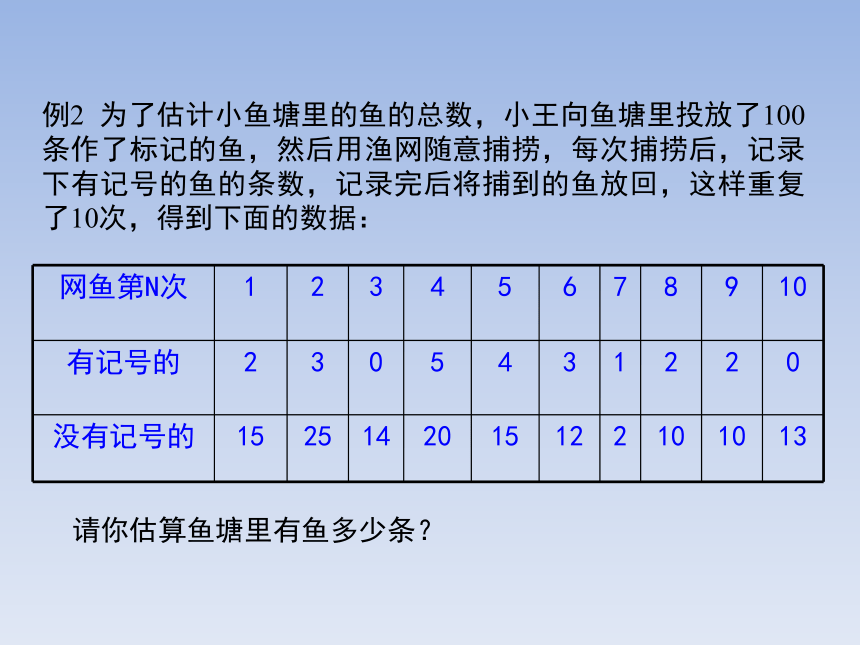
例2 为了估计小鱼塘里的鱼的总数,小王向鱼塘里投放了100条作了标记的鱼,然后用渔网随意捕捞,每次捕捞后,记录下有记号的鱼的条数,记录完后将捕到的鱼放回,这样重复了10次,得到下面的数据:
请你估算鱼塘里有鱼多少条?
网鱼第N次 1 2 3 4 5 6 7 8 9 10
有记号的 2 3 0 5 4 3 1 2 2 0
没有记号的 15 25 14 20 15 12 2 10 10 13
解:设估计鱼塘里有x条鱼
∴x≈618
答:鱼塘里大约有鱼618条.
x
100
136
22
=
灯泡个数 20 40 100 200 400 1000
使用寿命≥10000h的灯泡个数 19 37 93 179 361 902
合格率
某工厂新生产一种节能灯泡,设计使用寿命为10 000 h,现从第一批的大量产品中抽取若干个,在同等条件下进行使用寿命检验,有关数据如下:
(1)使用寿命≥10 000 h的灯泡为合格产品,计算各批灯泡的合格频率; (2)根据频率的稳定性估计灯泡的合格概率.(精确到0.1)
解:
(1)19÷20=0.95,37÷40=0.925,
93÷100=0.93,179÷200=0.895,
361÷400=0.903,902÷1000=0.902.
分析:(1)直接用频率的计算公式计算后填表; (2)根据各样品中灯泡的合格频率求其平均值.
(2)从上面的数据可以看出合格频率稳定在(0.95+0.925+0.93+0.895+0.903+0.902)÷6≈0.9附近,估计第一批灯泡的合格率为0.9.
灯泡个数
20 40 100 200 400 1000
使用寿命≥10000h的灯泡的个数 19 37 93 179 361 902
合格率
0.95
0.925
0.93
0.895
0.902
0.903
1.有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了
估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从
中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述
过程后,发现摸到红球的频率约为0.6,据此可以估计红球的个
数约为 个.
600
2.在同样条件下对某种小麦种子进行发芽实验,统计发芽种子
数,获得如下频数分布表:
实验种子n(粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数m(粒) 0 4 45 92 188 476 951 1900 2850
发芽频数m/n 0
(1)计算表中各个频数.
(2)估计该麦种的发芽概率
0.8
0.95
0.95
0.95
0.951
0.952
0.94
0.92
0.9
解:设估计鱼塘里有x条鱼,
则:
10
——=
100
50
——
x
∴x=500(条)(检验)
答:池塘中总共有约500条,共重1080千克.
216
——
100
=1080(千克)
3.“养鱼大王”老张为了与销售商签订购销合同,需要对自己鱼塘中鱼的总重量进行估计。为此,他先从鱼池中捞出50条鱼,将每条鱼做上记号放入水中;当它们完全混合于鱼群后,又捞出100条,称得重量为216千克,且带有记号的鱼为10条。问:老张的鱼塘中估计有多少条鱼?共重多少千克?
500×
4.张小明承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有两批幼苗可以选择,它们的成活率如下两个表格所示: A类树苗: B类树苗:
移植总数(m) 成活数(m) 成活的频率(m/n)
10 8
50 47
270 235
400 369
750 662
1500 1335
3500 3203
7000 6335
14000 12628
0.8
0.94
0.923
0.870
0.883
0.890
0.915
0.905
0.902
移植总数(m) 成活数(m) 成活的频率(m/n)
10 9
50 49
270 230
400 360
750 641
1500 1275
3500 2996
7000 5985
14000 11914
0.9
0.98
0.85
0.9
0.855
0.850
0.856
0.855
0.851
(1)从表中可以发现,A类幼树移植成活的频率在_____左右摆动,并且随着统计数据的增加,这种规律愈加明显,估计A类幼树移植成活的概率为____,估计B类幼树移 植成活的概率为___. (2)张小明选择A类树苗,还是B类树苗呢?_____,若他的荒山需要10 000株树苗,则他实际需要进树苗_______株? (3)如果每株树苗9元,则小明买树苗共需________元.
0.9
0.9
0.85
A类
11 112
100 008
5.如图,长方形内有一不规则区域,现在玩投掷游戏,如果随机掷中长方形的300次中,有100次是落在不规则图形内.
(1)你能估计出掷中不规则图形的概率吗?
(2)若该长方形的面积为150,试估计不规则图形的面积.
50
利用概率解决生活中的实际问题.
挑战自我
某种子站需要根据不合格种子所占比例,对新进的一批稻米种子进行定级,你能用频率估计概率的方法帮助种子站设计一个方案吗
第6章 事件的概率
6.5 事件的概率(2)
Contents
目录
01
02
03
04
学习目标
新课导入
当堂检测
课堂小结
典例探究
跟踪练习
05
06
1.了解随机事件发生的不确定性和概率的稳定性;
2.正确理解概率的含义,理解频率与概率的区别与联系;
3.利用概率解决生活中的实际问题.
频率与概率的关系
随着试验次数的增加, 频率会在概率的附近摆动,并趋于稳定.在实际问题中,若事件的概率未知,常用频率作为它的估计值.
频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同.而概率是一个确定数,是客观存在的,与每次试验无关.
(1)联系:
(2)区别:
例1 某林场,要考察一种树苗移植后的成活率,对这种树苗移植后成活情况进行跟踪调查,并将结果经过整理后,根据选取不同容量样本,得出相应的成活频率,绘制成统计图,根据统计图,回答下面的问题:
(1)这种树苗成活的频率在什么数值附近 成活率估计为多少?
(2)该林场已经移植这种树苗5万株,估计能成活多少万株?
(3)如果计划成活18万这种树苗,那么还需要移植多少万株?
分析:(1)由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9; (2)5×成活率即为所求的成活的树苗棵树; (3)利用成活率求得需要树苗棵数,减去已移植树苗数即为所求的树苗的棵数.
解:(1)这种树苗成活的频率稳定在0.9,
成活的概率估计值为0.9. (2)估计这种树苗成活在5×0.9=4.5万棵; (3)18÷0.9-5=15, 答:该地区还需移植这种树苗约15万棵.
例2 为了估计小鱼塘里的鱼的总数,小王向鱼塘里投放了100条作了标记的鱼,然后用渔网随意捕捞,每次捕捞后,记录下有记号的鱼的条数,记录完后将捕到的鱼放回,这样重复了10次,得到下面的数据:
请你估算鱼塘里有鱼多少条?
网鱼第N次 1 2 3 4 5 6 7 8 9 10
有记号的 2 3 0 5 4 3 1 2 2 0
没有记号的 15 25 14 20 15 12 2 10 10 13
解:设估计鱼塘里有x条鱼
∴x≈618
答:鱼塘里大约有鱼618条.
x
100
136
22
=
灯泡个数 20 40 100 200 400 1000
使用寿命≥10000h的灯泡个数 19 37 93 179 361 902
合格率
某工厂新生产一种节能灯泡,设计使用寿命为10 000 h,现从第一批的大量产品中抽取若干个,在同等条件下进行使用寿命检验,有关数据如下:
(1)使用寿命≥10 000 h的灯泡为合格产品,计算各批灯泡的合格频率; (2)根据频率的稳定性估计灯泡的合格概率.(精确到0.1)
解:
(1)19÷20=0.95,37÷40=0.925,
93÷100=0.93,179÷200=0.895,
361÷400=0.903,902÷1000=0.902.
分析:(1)直接用频率的计算公式计算后填表; (2)根据各样品中灯泡的合格频率求其平均值.
(2)从上面的数据可以看出合格频率稳定在(0.95+0.925+0.93+0.895+0.903+0.902)÷6≈0.9附近,估计第一批灯泡的合格率为0.9.
灯泡个数
20 40 100 200 400 1000
使用寿命≥10000h的灯泡的个数 19 37 93 179 361 902
合格率
0.95
0.925
0.93
0.895
0.902
0.903
1.有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了
估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从
中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述
过程后,发现摸到红球的频率约为0.6,据此可以估计红球的个
数约为 个.
600
2.在同样条件下对某种小麦种子进行发芽实验,统计发芽种子
数,获得如下频数分布表:
实验种子n(粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数m(粒) 0 4 45 92 188 476 951 1900 2850
发芽频数m/n 0
(1)计算表中各个频数.
(2)估计该麦种的发芽概率
0.8
0.95
0.95
0.95
0.951
0.952
0.94
0.92
0.9
解:设估计鱼塘里有x条鱼,
则:
10
——=
100
50
——
x
∴x=500(条)(检验)
答:池塘中总共有约500条,共重1080千克.
216
——
100
=1080(千克)
3.“养鱼大王”老张为了与销售商签订购销合同,需要对自己鱼塘中鱼的总重量进行估计。为此,他先从鱼池中捞出50条鱼,将每条鱼做上记号放入水中;当它们完全混合于鱼群后,又捞出100条,称得重量为216千克,且带有记号的鱼为10条。问:老张的鱼塘中估计有多少条鱼?共重多少千克?
500×
4.张小明承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有两批幼苗可以选择,它们的成活率如下两个表格所示: A类树苗: B类树苗:
移植总数(m) 成活数(m) 成活的频率(m/n)
10 8
50 47
270 235
400 369
750 662
1500 1335
3500 3203
7000 6335
14000 12628
0.8
0.94
0.923
0.870
0.883
0.890
0.915
0.905
0.902
移植总数(m) 成活数(m) 成活的频率(m/n)
10 9
50 49
270 230
400 360
750 641
1500 1275
3500 2996
7000 5985
14000 11914
0.9
0.98
0.85
0.9
0.855
0.850
0.856
0.855
0.851
(1)从表中可以发现,A类幼树移植成活的频率在_____左右摆动,并且随着统计数据的增加,这种规律愈加明显,估计A类幼树移植成活的概率为____,估计B类幼树移 植成活的概率为___. (2)张小明选择A类树苗,还是B类树苗呢?_____,若他的荒山需要10 000株树苗,则他实际需要进树苗_______株? (3)如果每株树苗9元,则小明买树苗共需________元.
0.9
0.9
0.85
A类
11 112
100 008
5.如图,长方形内有一不规则区域,现在玩投掷游戏,如果随机掷中长方形的300次中,有100次是落在不规则图形内.
(1)你能估计出掷中不规则图形的概率吗?
(2)若该长方形的面积为150,试估计不规则图形的面积.
50
利用概率解决生活中的实际问题.
挑战自我
某种子站需要根据不合格种子所占比例,对新进的一批稻米种子进行定级,你能用频率估计概率的方法帮助种子站设计一个方案吗
