四年级下学期数学第三单元第2课时《加法运算定律的运用》课件(共17张PPT)人教版
文档属性
| 名称 | 四年级下学期数学第三单元第2课时《加法运算定律的运用》课件(共17张PPT)人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
加法运算定律的运用
第三单元 运算定律
输入标题
引导学生在掌握和理解加法交换律和结合律的基础上,能运用运算定律进行一些简便运算。
准备好了吗?一起去探索吧!
能用所学的知识灵活解决实际问题,培养运用意识,感受数学与现实生活的联系。
培养学生根据具体情况,选择算法的意识与能力,增强数感,发展思维的灵活性。
学习目标
一级标题
输入标题
加法交换律:
加法结合律:(a+b)+c= a+(b+c)
复习回顾
上节课我们学习了什么?
改变加数的位置
使用小括号,改变加法的运算顺序
a+b=b+a
输入标题
提出问题
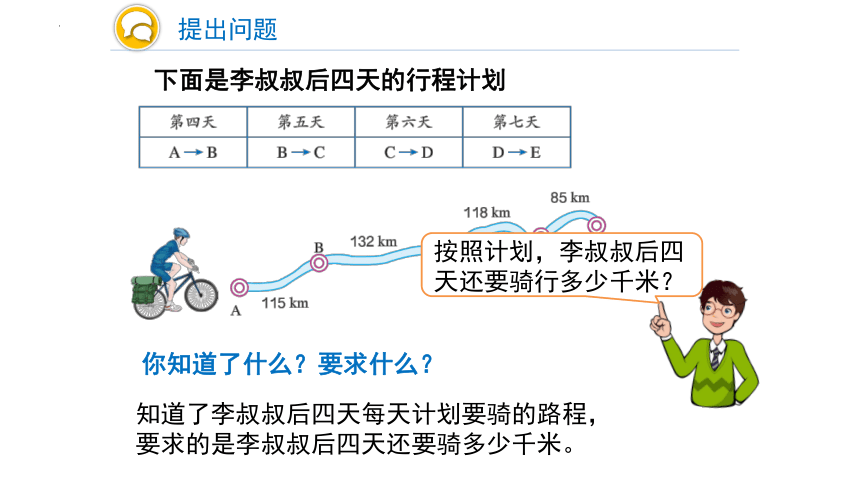
下面是李叔叔后四天的行程计划
你知道了什么?要求什么?
知道了李叔叔后四天每天计划要骑的路程,要求的是李叔叔后四天还要骑多少千米。
按照计划,李叔叔后四天还要骑行多少千米?
输入标题
你喜欢哪一种计算。
李叔叔后四天还要骑多少千米。
方法一
115+132+118+85
= 247+118+85
= 365+85
= 450(千米)
方法二
115+132+118+85
= 115+85+132+118
=(115+85)+(132+118)
= 200+250
= 450(千米)
解决问题
喜欢第2种方法,用了加法交换律和加法结合律。
一级标题
输入标题
从左往右依次计算
方法一
115+132+118+85
=247+118+85
=365+85
=450(千米)
方法二
115+132+118+85
=115+85+132+118
=(115+85)+(132+118)
=200+250
=450(千米)
加法交换律
加法结合律
分析问题
李叔叔后四天还要骑多少千米。
一级标题
输入标题
方法一
115+132+118+85
=247+118+85
=365+85
=450(千米)
方法二
115+132+118+85
=115+85+132+118
=(115+85)+(132+118)
=200+250
=450(千米)
在一个加法算式中,如果某些加数可以凑成整十、整百或几百几十的数……,运用加法交换律和结合律改变运算顺序,把它们先相加,可以使计算更加简便。
总结方法
(a+178)+13= a+(178+13)运用了加法结合律。
( )
练习
输入标题
1. 判断。(对的打“√”,错的画“×”)
√
63+34=34+63运用了加法交换律。( )
138+65+62=65+(138+62)只运用了加法交换律。( )
√
×
187+a+13=187+13+a只运用了加法交换律。( )
√
(1)
(2)
(3)
(4)
2. 哪个算式计算最简便。
一级标题
输入标题
C
(1) 78+157+22 ( )
A 78+(157+22)
B 157+(78+22)
C (78+157)+22
B
(2)91+43+109+57 ( )
A ( 91+43)+(109+57)
B 91+(43+57)+109
C (91+109)+(43+57)
练习
3.
输入标题
王阿姨一共要汇多少钱?
225+328+175
= 225 +175+ 328
= 400+328
= 728(元)
练习
答:王阿姨一共要汇728元。
一级标题
输入标题
4.这堆原木一共有多少根?
方法一
答:这堆原木一共有55根。
10+9+8+7+6+5+4+3+2+1
= 10+(9+1)+(8+2)+(7+3)+(6+4)+5
= 10+10+10+10+10+5
= 55(根)
把能凑成整十的数结合先加
练习
一级标题
输入标题
方法二
答:这堆原木一共有55根。
10+9+8+7+6+5+4+3+2+1
=(10+1)+(9+2)+(8+3)+(7+4)+(6+5)
=11+11+11+11+11
=11×5
=55(根)
每两个数的和都等于第一个数与最后一个数的和,10个数中共有这样的5对。
练习
4.这堆原木一共有多少根?
输入标题
你有什么收获?
2.在计算加法时,要先观察数据的特点,运用加法的运算定律把可以凑成整十、整百、几百几十……的数先相加,可以使计算简便。
1.加法交换律改变加数的位置,加法结合律使用小括号,改变加法的运算顺序,它们可以使计算更加简便。
一级标题
输入标题
教材P23练习六
第8、9题
输入标题
拓展延伸
1+2+3+4+5+ +99+100 的和是多少的故事吗?
同学们,你们听说过数学家高斯小时候计算:
因为1+100=101, 2+99=101, 3+98=101, ……,
49+52=101, 50+51=101,而像这样和是101的的组合一共有50组,所以很快就可以求出:101×50=5050。
高斯这样解释:
=(1+100)+(2+99)+(3+98)+ +(50+51)
=(1+100)×(100÷2)
=101×50
=5050
输入标题
拓展延伸
1+2+3+4+5+ +99+100
100个数,2个数一对,所以有(100÷2)对
再见
加法运算定律的运用
第三单元 运算定律
输入标题
引导学生在掌握和理解加法交换律和结合律的基础上,能运用运算定律进行一些简便运算。
准备好了吗?一起去探索吧!
能用所学的知识灵活解决实际问题,培养运用意识,感受数学与现实生活的联系。
培养学生根据具体情况,选择算法的意识与能力,增强数感,发展思维的灵活性。
学习目标
一级标题
输入标题
加法交换律:
加法结合律:(a+b)+c= a+(b+c)
复习回顾
上节课我们学习了什么?
改变加数的位置
使用小括号,改变加法的运算顺序
a+b=b+a
输入标题
提出问题
下面是李叔叔后四天的行程计划
你知道了什么?要求什么?
知道了李叔叔后四天每天计划要骑的路程,要求的是李叔叔后四天还要骑多少千米。
按照计划,李叔叔后四天还要骑行多少千米?
输入标题
你喜欢哪一种计算。
李叔叔后四天还要骑多少千米。
方法一
115+132+118+85
= 247+118+85
= 365+85
= 450(千米)
方法二
115+132+118+85
= 115+85+132+118
=(115+85)+(132+118)
= 200+250
= 450(千米)
解决问题
喜欢第2种方法,用了加法交换律和加法结合律。
一级标题
输入标题
从左往右依次计算
方法一
115+132+118+85
=247+118+85
=365+85
=450(千米)
方法二
115+132+118+85
=115+85+132+118
=(115+85)+(132+118)
=200+250
=450(千米)
加法交换律
加法结合律
分析问题
李叔叔后四天还要骑多少千米。
一级标题
输入标题
方法一
115+132+118+85
=247+118+85
=365+85
=450(千米)
方法二
115+132+118+85
=115+85+132+118
=(115+85)+(132+118)
=200+250
=450(千米)
在一个加法算式中,如果某些加数可以凑成整十、整百或几百几十的数……,运用加法交换律和结合律改变运算顺序,把它们先相加,可以使计算更加简便。
总结方法
(a+178)+13= a+(178+13)运用了加法结合律。
( )
练习
输入标题
1. 判断。(对的打“√”,错的画“×”)
√
63+34=34+63运用了加法交换律。( )
138+65+62=65+(138+62)只运用了加法交换律。( )
√
×
187+a+13=187+13+a只运用了加法交换律。( )
√
(1)
(2)
(3)
(4)
2. 哪个算式计算最简便。
一级标题
输入标题
C
(1) 78+157+22 ( )
A 78+(157+22)
B 157+(78+22)
C (78+157)+22
B
(2)91+43+109+57 ( )
A ( 91+43)+(109+57)
B 91+(43+57)+109
C (91+109)+(43+57)
练习
3.
输入标题
王阿姨一共要汇多少钱?
225+328+175
= 225 +175+ 328
= 400+328
= 728(元)
练习
答:王阿姨一共要汇728元。
一级标题
输入标题
4.这堆原木一共有多少根?
方法一
答:这堆原木一共有55根。
10+9+8+7+6+5+4+3+2+1
= 10+(9+1)+(8+2)+(7+3)+(6+4)+5
= 10+10+10+10+10+5
= 55(根)
把能凑成整十的数结合先加
练习
一级标题
输入标题
方法二
答:这堆原木一共有55根。
10+9+8+7+6+5+4+3+2+1
=(10+1)+(9+2)+(8+3)+(7+4)+(6+5)
=11+11+11+11+11
=11×5
=55(根)
每两个数的和都等于第一个数与最后一个数的和,10个数中共有这样的5对。
练习
4.这堆原木一共有多少根?
输入标题
你有什么收获?
2.在计算加法时,要先观察数据的特点,运用加法的运算定律把可以凑成整十、整百、几百几十……的数先相加,可以使计算简便。
1.加法交换律改变加数的位置,加法结合律使用小括号,改变加法的运算顺序,它们可以使计算更加简便。
一级标题
输入标题
教材P23练习六
第8、9题
输入标题
拓展延伸
1+2+3+4+5+ +99+100 的和是多少的故事吗?
同学们,你们听说过数学家高斯小时候计算:
因为1+100=101, 2+99=101, 3+98=101, ……,
49+52=101, 50+51=101,而像这样和是101的的组合一共有50组,所以很快就可以求出:101×50=5050。
高斯这样解释:
=(1+100)+(2+99)+(3+98)+ +(50+51)
=(1+100)×(100÷2)
=101×50
=5050
输入标题
拓展延伸
1+2+3+4+5+ +99+100
100个数,2个数一对,所以有(100÷2)对
再见
