四年级下学期数学第三单元第6课时《解决问题策略多样化(简便计算)》课件(共16张PPT)
文档属性
| 名称 | 四年级下学期数学第三单元第6课时《解决问题策略多样化(简便计算)》课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 13:42:40 | ||
图片预览






文档简介
(共16张PPT)
解决问题策略多样化(简便计算)
第三单元 运算定律
输入标题
学习目标
通过灵活、合理的简便算法调动学生学习的积极性。
经历运算定律的应用过程,培养学生思维的灵活性,提升学生解题策略多样性的能力。
准备好了吗?一起去探索吧!
能灵活运用乘法的运算定律进行简便计算,理解和掌握连除算式的简便计算方法。
一级标题
输入标题
运算定律
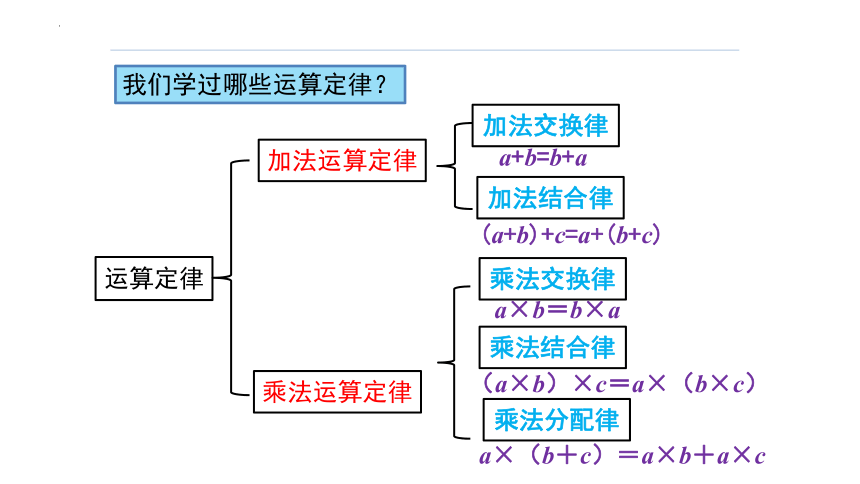
我们学过哪些运算定律?
加法运算定律
乘法运算定律
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
a×(b+c)=a×b+a×c
尝试解决,展示算法
王老师买了5副羽毛球拍,花了330元,还买了25筒羽毛球,每筒32元。
一筒有12个羽毛球哦
王老师一共买了多少个羽毛球?请列出算式。
12×25=
尝试解决,展示算法
12×25=
你能又快又准确地计算出结果吗?请试一试。
6 0
1 2
2 5
×
2 4
3 0 0
12×25=
300
方法一:
12×25
=(3×4)×25
=3×(4×25)
=3×100
=300
方法二:
12×25
=(10+2)×25
=10×25+2×25
=250+50
=300
方法三:
乘法结合律
乘法分配律
竖式计算
对比思考
12×25
=(3×4)×25
=3×(4×25)
=3×100
=300
12×25
=(10+2)×25
=10×25+2×25
=250+50
=300
乘法结合律
乘法分配律
仔细观察这两种计算的方法,有什么相同的地方?
都是先拆数,再用运算定律进行简便计算。
做一做
用简便方法计算。
48×25
48×25
=(12×4)×25
=12×(4×25)
=12×100
=1200
48×25
=(40+8)×25
=40×25+8×25
=1000+200
=1200
方法一:
方法二:
乘法结合律
乘法分配律
=1200
103×24
做一做
用简便方法计算。
103×24
=103×(4×6)
=103×4×6
=412×6
=2472
103×24
=(100+3)×24
=100×24+3×24
=2400+72
=2472
方法一:
方法二:
乘法结合律
乘法分配律
计算103×24时,哪种方法更加简便?
第二种更加简便,因为凑成整百数更容易计算。
=2472
归纳小结
拆数凑整时,不仅可以拆乘,还可以拆加。像计算48×25时,拆乘,可以运用乘法结合律来进行简便运算。拆加,可以运用乘法分配律来进行简便运算。需要我们根据数据特征进行合理的选择。
48×25
=(12×4)×25
=12×(4×25)
=12×100
=1200
48×25
=(40+8)×25
=40×25+8×25
=1000+200
=1200
乘法结合律
乘法分配律
尝试计算,展示算法
330÷5÷2 =
330÷5÷2
=66÷2
=33
330÷5÷2
=330÷(5×2)
=330÷10
=33
方法一:
方法二:
每支羽毛球拍多少钱?
王老师买了5副羽毛拍,花了330元,还买了25筒羽毛球,每筒32元。
借助题意,发现规律
330÷5÷2
=330÷(5×2)
=330÷10
=33
方法二:
第二种方法可以怎样理解?
一个数连续除以两个数,可以除以这两个数的积,这叫做除法的性质。
a÷b÷c=a÷(b×c)
先计算一共有多少支羽毛球拍,再算每支羽毛球拍多少钱。
先算2乘5是为了凑整,再算330除以10可以使计算更加简便。因此,我们可以说330÷5÷2等于 330÷(5×2)。
一级标题
1.计算下面各题,怎样简便就怎样计算。
3000÷25÷4
=3000÷(25×4)
=3000÷100
=30
4200÷42÷2
125×88
=100÷2
=50
=125×(8×11)
=125×8×11
=1000×11
=11000
125×88
=125×(80+8)
=125×80+125×8
=10000+1000
=11000
练习
一级标题
2.解决问题
奶牛场养了25头奶牛,每头奶牛每天吃草13千克。照这样计算。1400千克的草,够它们吃4天吗?
25×13×4
= 25×4×13
= 100×13
= 1300(千克)
1300千克<1400千克
1400÷(25×13)
= 1400÷325
= 4(天)……100(千克)
方法一:
方法二:
答:1400千克的草够它们吃4天。
同一个问题,解决的策略不同,计算方法也就不同。
练习
一级标题
你有什么收获?
在简便计算时,要根据数据的特点找到合理的方法,进行灵活运算。
一个数连续除以两个数,可以除以这两个数的积,这叫做除法的性质。
用字母表示为:
a÷b÷c=a÷(b×c)
一级标题
输入标题
教材P30第1、3、5题。
再见
解决问题策略多样化(简便计算)
第三单元 运算定律
输入标题
学习目标
通过灵活、合理的简便算法调动学生学习的积极性。
经历运算定律的应用过程,培养学生思维的灵活性,提升学生解题策略多样性的能力。
准备好了吗?一起去探索吧!
能灵活运用乘法的运算定律进行简便计算,理解和掌握连除算式的简便计算方法。
一级标题
输入标题
运算定律
我们学过哪些运算定律?
加法运算定律
乘法运算定律
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
a×(b+c)=a×b+a×c
尝试解决,展示算法
王老师买了5副羽毛球拍,花了330元,还买了25筒羽毛球,每筒32元。
一筒有12个羽毛球哦
王老师一共买了多少个羽毛球?请列出算式。
12×25=
尝试解决,展示算法
12×25=
你能又快又准确地计算出结果吗?请试一试。
6 0
1 2
2 5
×
2 4
3 0 0
12×25=
300
方法一:
12×25
=(3×4)×25
=3×(4×25)
=3×100
=300
方法二:
12×25
=(10+2)×25
=10×25+2×25
=250+50
=300
方法三:
乘法结合律
乘法分配律
竖式计算
对比思考
12×25
=(3×4)×25
=3×(4×25)
=3×100
=300
12×25
=(10+2)×25
=10×25+2×25
=250+50
=300
乘法结合律
乘法分配律
仔细观察这两种计算的方法,有什么相同的地方?
都是先拆数,再用运算定律进行简便计算。
做一做
用简便方法计算。
48×25
48×25
=(12×4)×25
=12×(4×25)
=12×100
=1200
48×25
=(40+8)×25
=40×25+8×25
=1000+200
=1200
方法一:
方法二:
乘法结合律
乘法分配律
=1200
103×24
做一做
用简便方法计算。
103×24
=103×(4×6)
=103×4×6
=412×6
=2472
103×24
=(100+3)×24
=100×24+3×24
=2400+72
=2472
方法一:
方法二:
乘法结合律
乘法分配律
计算103×24时,哪种方法更加简便?
第二种更加简便,因为凑成整百数更容易计算。
=2472
归纳小结
拆数凑整时,不仅可以拆乘,还可以拆加。像计算48×25时,拆乘,可以运用乘法结合律来进行简便运算。拆加,可以运用乘法分配律来进行简便运算。需要我们根据数据特征进行合理的选择。
48×25
=(12×4)×25
=12×(4×25)
=12×100
=1200
48×25
=(40+8)×25
=40×25+8×25
=1000+200
=1200
乘法结合律
乘法分配律
尝试计算,展示算法
330÷5÷2 =
330÷5÷2
=66÷2
=33
330÷5÷2
=330÷(5×2)
=330÷10
=33
方法一:
方法二:
每支羽毛球拍多少钱?
王老师买了5副羽毛拍,花了330元,还买了25筒羽毛球,每筒32元。
借助题意,发现规律
330÷5÷2
=330÷(5×2)
=330÷10
=33
方法二:
第二种方法可以怎样理解?
一个数连续除以两个数,可以除以这两个数的积,这叫做除法的性质。
a÷b÷c=a÷(b×c)
先计算一共有多少支羽毛球拍,再算每支羽毛球拍多少钱。
先算2乘5是为了凑整,再算330除以10可以使计算更加简便。因此,我们可以说330÷5÷2等于 330÷(5×2)。
一级标题
1.计算下面各题,怎样简便就怎样计算。
3000÷25÷4
=3000÷(25×4)
=3000÷100
=30
4200÷42÷2
125×88
=100÷2
=50
=125×(8×11)
=125×8×11
=1000×11
=11000
125×88
=125×(80+8)
=125×80+125×8
=10000+1000
=11000
练习
一级标题
2.解决问题
奶牛场养了25头奶牛,每头奶牛每天吃草13千克。照这样计算。1400千克的草,够它们吃4天吗?
25×13×4
= 25×4×13
= 100×13
= 1300(千克)
1300千克<1400千克
1400÷(25×13)
= 1400÷325
= 4(天)……100(千克)
方法一:
方法二:
答:1400千克的草够它们吃4天。
同一个问题,解决的策略不同,计算方法也就不同。
练习
一级标题
你有什么收获?
在简便计算时,要根据数据的特点找到合理的方法,进行灵活运算。
一个数连续除以两个数,可以除以这两个数的积,这叫做除法的性质。
用字母表示为:
a÷b÷c=a÷(b×c)
一级标题
输入标题
教材P30第1、3、5题。
再见
