人教版七年级下册 8.2 消元——解二元一次方程组课件(共17张PPT)
文档属性
| 名称 | 人教版七年级下册 8.2 消元——解二元一次方程组课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 274.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 22:33:06 | ||
图片预览





文档简介
(共17张PPT)
8.2消元——解二元一次方程组
加减消元法(第二课时)
复习导入
化简:
解:
去分母(易错处:每一项都乘最小公倍数)
去括号(注意括号前为负数时,符号的变化)
合并同类项
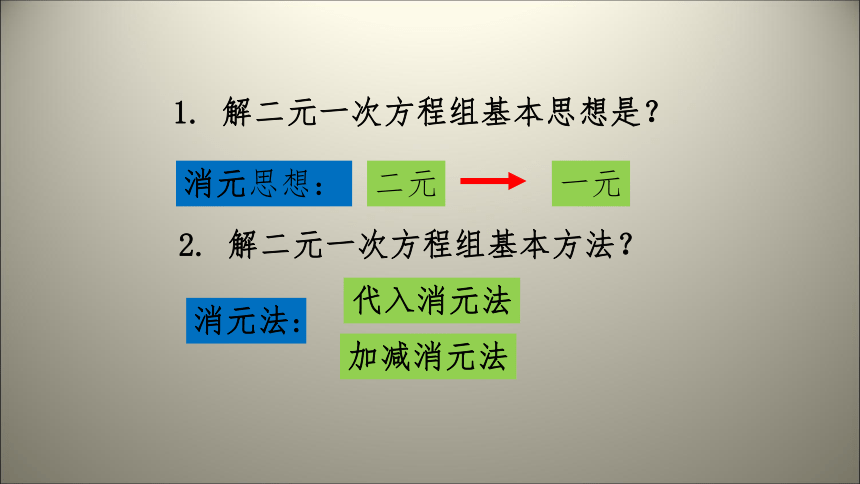
消元思想:
二元
一元
1. 解二元一次方程组基本思想是?
2. 解二元一次方程组基本方法?
消元法:
代入消元法
加减消元法
例题1:解方程组
2x+ 3y = 16
5x - 6y = 33
①
②
问题1:这两个方程直接相加减能消去未知数吗?为什么?
问题2:怎样使方程组中某一未知数的系数相同或相反呢?
1.先确定消去哪个未知数;
2.再找出系数的最小公倍数;
3.确定每一个方程两边应同乘以几。
先消去哪个未知数比较 方便呢?
探索新知
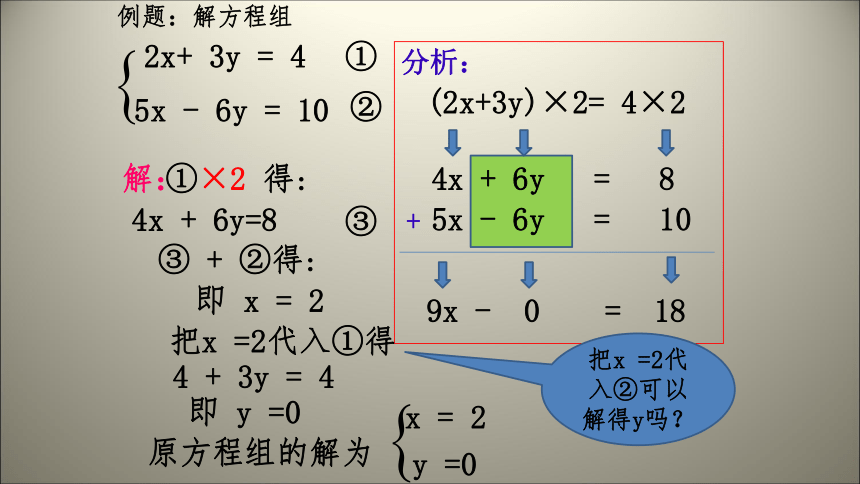
例题:解方程组
2x+ 3y = 4
5x - 6y = 10
①
②
分析:
4x + 6y = 8
5x - 6y = 10
(2x+3y)×2= 4×2
9x - 0 = 18
原方程组的解为
y =0
x = 2
解:
①×2 得:
即 x = 2
4x + 6y=8
③ + ②得:
③
4 + 3y = 4
即 y =0
把x =2代入①得
把x =2代入②可以解得y吗?
+
例题:解方程组
2x+ 3y = 4
5x - 6y = 10
①
②
解:
①×2 得:
原方程组的解为
即 x = 2
4 + 3y = 4
4x + 6y=8
③ + ②得:
y =0
x = 2
即 y =0
③
把x =2代入①得
一般步骤:
1.变形
3.解一元一次方程
2.加减消元
4.回代
5.写解
例2:用加减法解方程组
19x = 114
即 x = 6
③ + ④ 得:
原方程组的解为
y =
x = 6
1
2
把x = 6代入①得
18 + 4y = 16
即 y =
1
2
解:
①×3 得:
9x + 12y = 48
②×2 得:
10x - 12y = 66
④
③
3x+ 4y = 16
5x - 6y = 33
①
②
一般步骤:
1.变形
2.加减消元,求解
3.回代
4.写解
例2:用加减法解 方程组
3x + 4y = 16
5x - 6y = 33
解:
原方程组的解为
y =
x = 6
1
2
38y = -19
即 y =
③ - ④ 得:
1
2
①×5 得:
15x+ 20y = 80
②×3 得:
15x - 18y = 99
④
③
①
②
思考:如果用加减法消去x,应如何解呢?
把y = 代入①得
3x + 4 × ( ) = 16
即 x =6
1
2
1
2
练测促学
随堂练习:用加减消元法解方程组:
2x+y=5 ①
x+y=3 ②
(1)
① - ②
① + ②
直接相加或相减
2x+y=7 ①
x-y=2 ②
(2)
5x – 2y = 25 ①
3x +4y=15 ②
1、用加减法解下列方程组:
课堂练习
2x +3y = 16 ①
3x -2y=-2 ②
则x+y= 。
2、已知:
3x + 2y =8
2x +3y =12
4
2、选择适当的方法解方程组
(1) y=2x
3x-4y=5
(2) x-2y=y+1
2x-3y=10
代入法
代入或加减法
(3) 3(x-1)=y+5
5(y-1)=3(x+5)
代入或加减法
(4)
加减法
2、选择适当的方法解方程组
自我提升
1、已知方程组 中,①+②,得 ,解得x= .
2、解方程组 ,发现x的系数特点是 ,
只要将这两个方程相 ,便可消去未知数 。
5x=5
1
相同
减
x
解关于x、y的方程组 ,
求得正确的解是 ,
而因看错系数 c 解得 ,
试求a,b,c的值。
a=4,b=5,c=-2
拓展练习
扩展应用:观察
4x+8y=12
3x-2y=5
(2)
y- x = 1
3x + 2y = 5
(1)
问题:
你能体会这两种方法各自在什么情况下使用较方便吗?
目前,我们已经学习了两种消元法,以上两种方程组各用什么方法较简单?
达标检测,当场检测
生活中灵活运用
写解
解一元一次方程
加减消元
二元变一元
回代
课堂小结 :
用加减法解二元一次方程组的一般步骤:
变形
最小公倍数
8.2消元——解二元一次方程组
加减消元法(第二课时)
复习导入
化简:
解:
去分母(易错处:每一项都乘最小公倍数)
去括号(注意括号前为负数时,符号的变化)
合并同类项
消元思想:
二元
一元
1. 解二元一次方程组基本思想是?
2. 解二元一次方程组基本方法?
消元法:
代入消元法
加减消元法
例题1:解方程组
2x+ 3y = 16
5x - 6y = 33
①
②
问题1:这两个方程直接相加减能消去未知数吗?为什么?
问题2:怎样使方程组中某一未知数的系数相同或相反呢?
1.先确定消去哪个未知数;
2.再找出系数的最小公倍数;
3.确定每一个方程两边应同乘以几。
先消去哪个未知数比较 方便呢?
探索新知
例题:解方程组
2x+ 3y = 4
5x - 6y = 10
①
②
分析:
4x + 6y = 8
5x - 6y = 10
(2x+3y)×2= 4×2
9x - 0 = 18
原方程组的解为
y =0
x = 2
解:
①×2 得:
即 x = 2
4x + 6y=8
③ + ②得:
③
4 + 3y = 4
即 y =0
把x =2代入①得
把x =2代入②可以解得y吗?
+
例题:解方程组
2x+ 3y = 4
5x - 6y = 10
①
②
解:
①×2 得:
原方程组的解为
即 x = 2
4 + 3y = 4
4x + 6y=8
③ + ②得:
y =0
x = 2
即 y =0
③
把x =2代入①得
一般步骤:
1.变形
3.解一元一次方程
2.加减消元
4.回代
5.写解
例2:用加减法解方程组
19x = 114
即 x = 6
③ + ④ 得:
原方程组的解为
y =
x = 6
1
2
把x = 6代入①得
18 + 4y = 16
即 y =
1
2
解:
①×3 得:
9x + 12y = 48
②×2 得:
10x - 12y = 66
④
③
3x+ 4y = 16
5x - 6y = 33
①
②
一般步骤:
1.变形
2.加减消元,求解
3.回代
4.写解
例2:用加减法解 方程组
3x + 4y = 16
5x - 6y = 33
解:
原方程组的解为
y =
x = 6
1
2
38y = -19
即 y =
③ - ④ 得:
1
2
①×5 得:
15x+ 20y = 80
②×3 得:
15x - 18y = 99
④
③
①
②
思考:如果用加减法消去x,应如何解呢?
把y = 代入①得
3x + 4 × ( ) = 16
即 x =6
1
2
1
2
练测促学
随堂练习:用加减消元法解方程组:
2x+y=5 ①
x+y=3 ②
(1)
① - ②
① + ②
直接相加或相减
2x+y=7 ①
x-y=2 ②
(2)
5x – 2y = 25 ①
3x +4y=15 ②
1、用加减法解下列方程组:
课堂练习
2x +3y = 16 ①
3x -2y=-2 ②
则x+y= 。
2、已知:
3x + 2y =8
2x +3y =12
4
2、选择适当的方法解方程组
(1) y=2x
3x-4y=5
(2) x-2y=y+1
2x-3y=10
代入法
代入或加减法
(3) 3(x-1)=y+5
5(y-1)=3(x+5)
代入或加减法
(4)
加减法
2、选择适当的方法解方程组
自我提升
1、已知方程组 中,①+②,得 ,解得x= .
2、解方程组 ,发现x的系数特点是 ,
只要将这两个方程相 ,便可消去未知数 。
5x=5
1
相同
减
x
解关于x、y的方程组 ,
求得正确的解是 ,
而因看错系数 c 解得 ,
试求a,b,c的值。
a=4,b=5,c=-2
拓展练习
扩展应用:观察
4x+8y=12
3x-2y=5
(2)
y- x = 1
3x + 2y = 5
(1)
问题:
你能体会这两种方法各自在什么情况下使用较方便吗?
目前,我们已经学习了两种消元法,以上两种方程组各用什么方法较简单?
达标检测,当场检测
生活中灵活运用
写解
解一元一次方程
加减消元
二元变一元
回代
课堂小结 :
用加减法解二元一次方程组的一般步骤:
变形
最小公倍数
