沪科版数学八年级下册 19.4 综合与实践 多边形的镶嵌-课件(共26张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.4 综合与实践 多边形的镶嵌-课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 774.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 13:02:29 | ||
图片预览






文档简介
(共26张PPT)
19.4 综合与实践 多边形的镶嵌
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
情景导入
请你欣赏
自主学习
用形状相同或不同的平面封闭图形,覆盖平面区域,
使图形间既无缝隙又不重叠地全部覆盖,叫做平面镶嵌.
注意:各种图形拼接后要既无缝隙,又不重叠.
定义:
合作探究
活动1:探究用一种正多边形
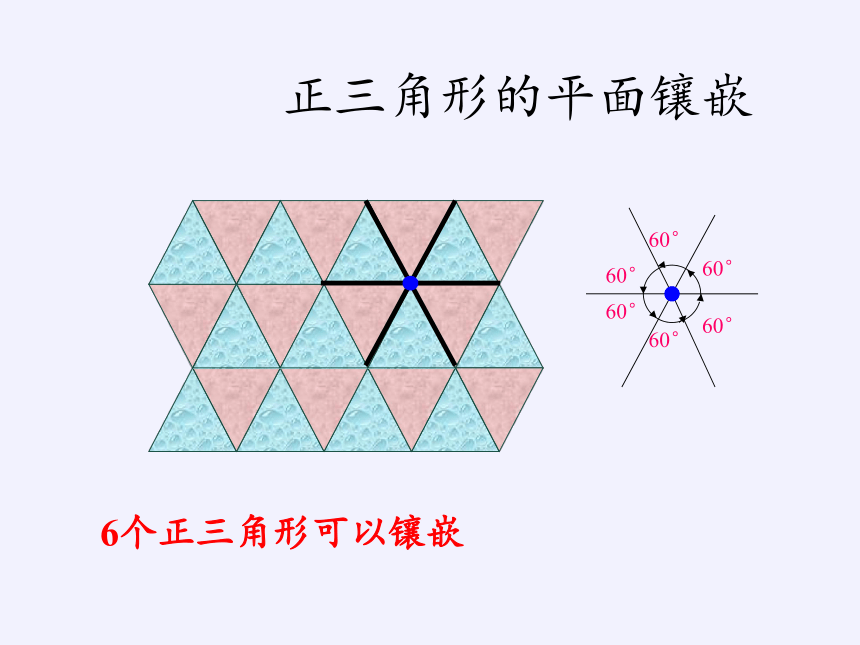
正三角形的平面镶嵌
60°
60°
60°
60°
60°
60°
6个正三角形可以镶嵌
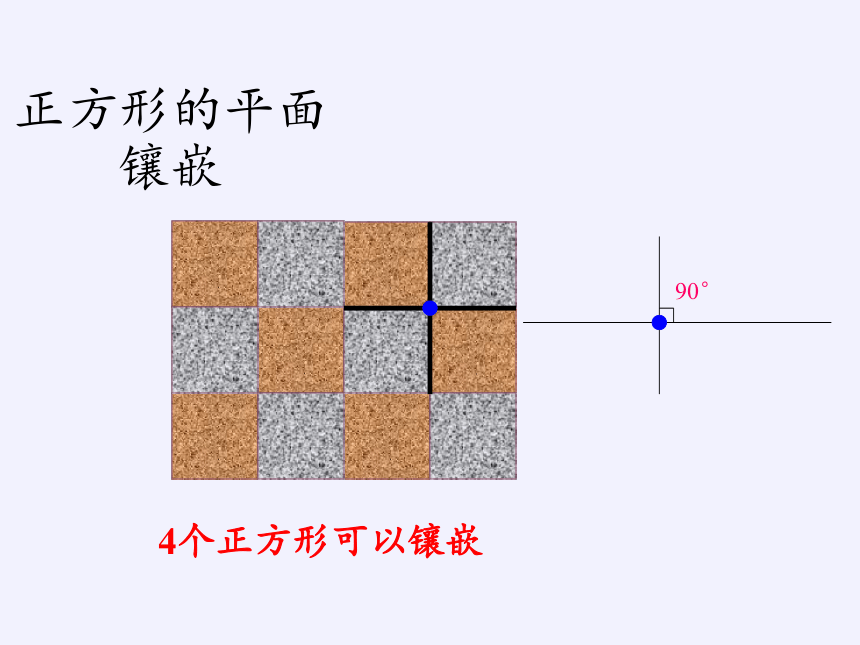
正方形的平面镶嵌
90°
4个正方形可以镶嵌
正六边形的平面镶嵌
120 °
120 °
120 °
3个正六边形可以镶嵌
1
2
3
∠1+∠2+∠3=
用正五边形能否镶嵌?
为什么正五边形不能镶嵌?
结论
要使图形不留空隙、不重叠地镶嵌一个平面区域,需使得拼接点处的所有内角之和等于360°.
思考
还有其它正多边形能镶嵌吗?
正多边形可以镶嵌的条件:
每个内角都能被360o 整除.
图形 一个顶点周围正多边形的个数
能
能
能
正三角形
正方形
正五边形
正六边形
6
4
3
不能
能否平
面镶嵌
90°
一个内
角度数
108°
60°
120°
2个正三角形+2个正六边形
活动2:探究同时用两种正多边形
3个正三角形+2个正方形
收获
当拼接点处的所有角之和是360 时,就能拼成一个平面图形.
用正三角形和正六边形作平面镶嵌,在一个顶点周围,正三角形与正六边形各需要多少个?
能否同时用正方形和正六边形作
平面镶嵌?
结论:
形状、大小完全相同的任意三角形能镶嵌成平面图形.
活动3:探究用一种非正多边形
形状、大小相同的任意四边形能镶嵌成
平面图形.
请你分别按下列要求设计一个多边形的镶嵌图案:
(1)只用一种多边形;
(2)同时用两种多边形;
(3)用一种非正多边形.
家庭作业
谢 谢
19.4 综合与实践 多边形的镶嵌
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
情景导入
请你欣赏
自主学习
用形状相同或不同的平面封闭图形,覆盖平面区域,
使图形间既无缝隙又不重叠地全部覆盖,叫做平面镶嵌.
注意:各种图形拼接后要既无缝隙,又不重叠.
定义:
合作探究
活动1:探究用一种正多边形
正三角形的平面镶嵌
60°
60°
60°
60°
60°
60°
6个正三角形可以镶嵌
正方形的平面镶嵌
90°
4个正方形可以镶嵌
正六边形的平面镶嵌
120 °
120 °
120 °
3个正六边形可以镶嵌
1
2
3
∠1+∠2+∠3=
用正五边形能否镶嵌?
为什么正五边形不能镶嵌?
结论
要使图形不留空隙、不重叠地镶嵌一个平面区域,需使得拼接点处的所有内角之和等于360°.
思考
还有其它正多边形能镶嵌吗?
正多边形可以镶嵌的条件:
每个内角都能被360o 整除.
图形 一个顶点周围正多边形的个数
能
能
能
正三角形
正方形
正五边形
正六边形
6
4
3
不能
能否平
面镶嵌
90°
一个内
角度数
108°
60°
120°
2个正三角形+2个正六边形
活动2:探究同时用两种正多边形
3个正三角形+2个正方形
收获
当拼接点处的所有角之和是360 时,就能拼成一个平面图形.
用正三角形和正六边形作平面镶嵌,在一个顶点周围,正三角形与正六边形各需要多少个?
能否同时用正方形和正六边形作
平面镶嵌?
结论:
形状、大小完全相同的任意三角形能镶嵌成平面图形.
活动3:探究用一种非正多边形
形状、大小相同的任意四边形能镶嵌成
平面图形.
请你分别按下列要求设计一个多边形的镶嵌图案:
(1)只用一种多边形;
(2)同时用两种多边形;
(3)用一种非正多边形.
家庭作业
谢 谢
