五年级下学期数学3.2长方体、正方体的表面积课件(共27张PPT)西师大版
文档属性
| 名称 | 五年级下学期数学3.2长方体、正方体的表面积课件(共27张PPT)西师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 17:28:36 | ||
图片预览




文档简介
(共27张PPT)
西师版五年级下册第三单元
长方体、正方体的表面积
你知道自己的生日是哪一天吗?你最想收到什么生日礼物呢?
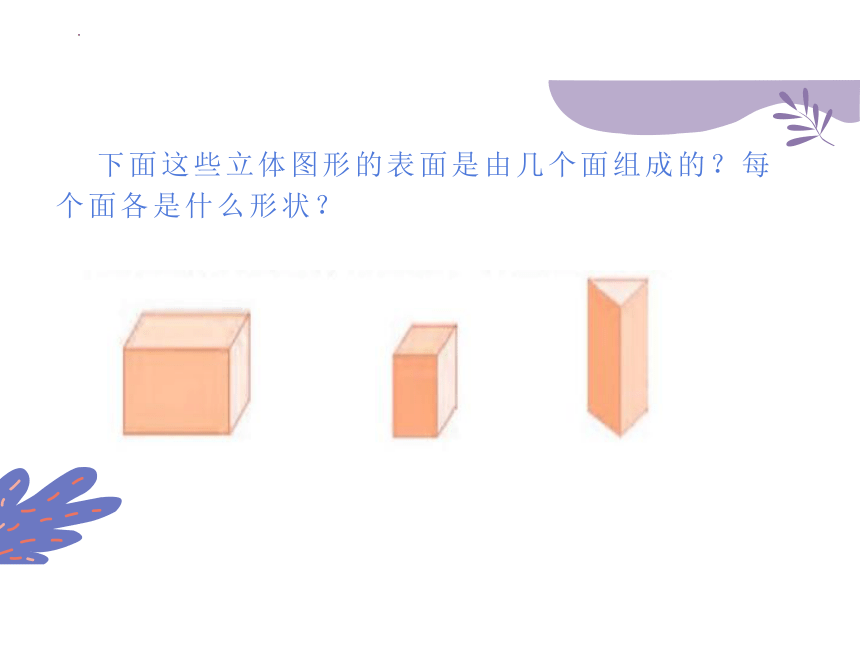
下面这些立体图形的表面是由几个面组成的?每个面各是什么形状?
长方体或正方体露在外面的部分,也就是这6个面,我们称为长方体或正方体的表面。
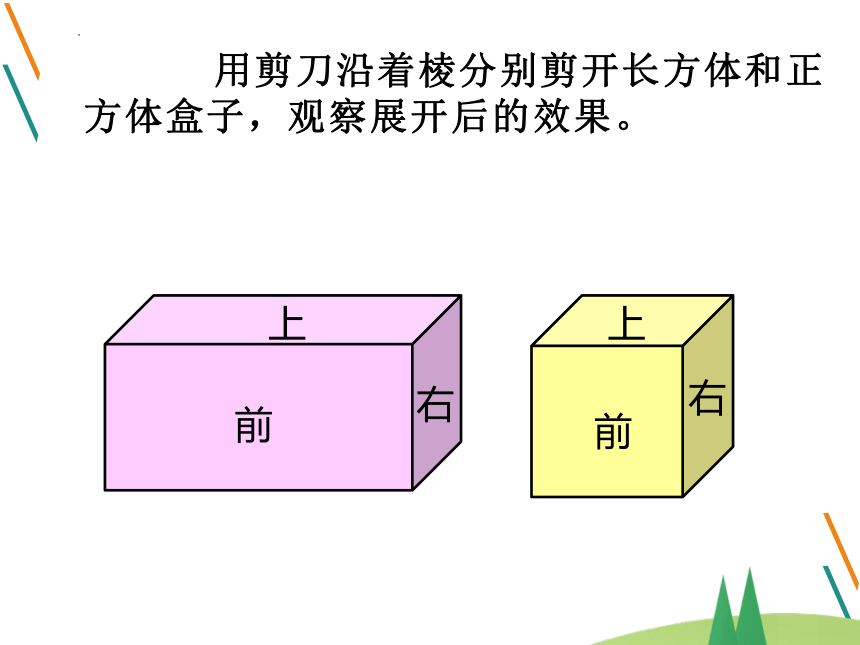
用剪刀沿着棱分别剪开长方体和正方体盒子,观察展开后的效果。
前
上
右
前
上
右
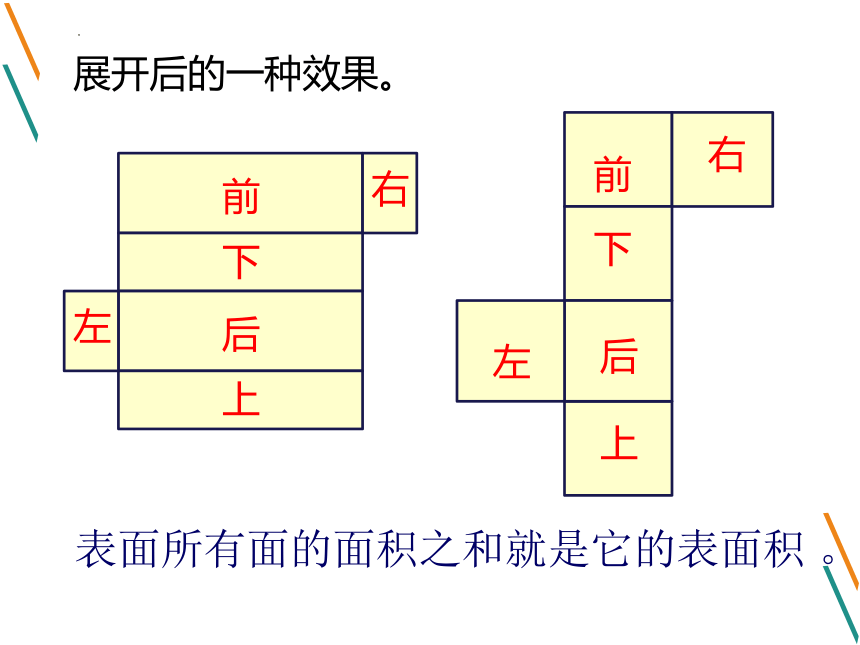
前
右
下
后
上
左
前
右
下
后
上
左
展开后的一种效果。
表面所有面的面积之和就是它的表面积 。
长方体或正方体6个面的面积之和,就是它的表面积。
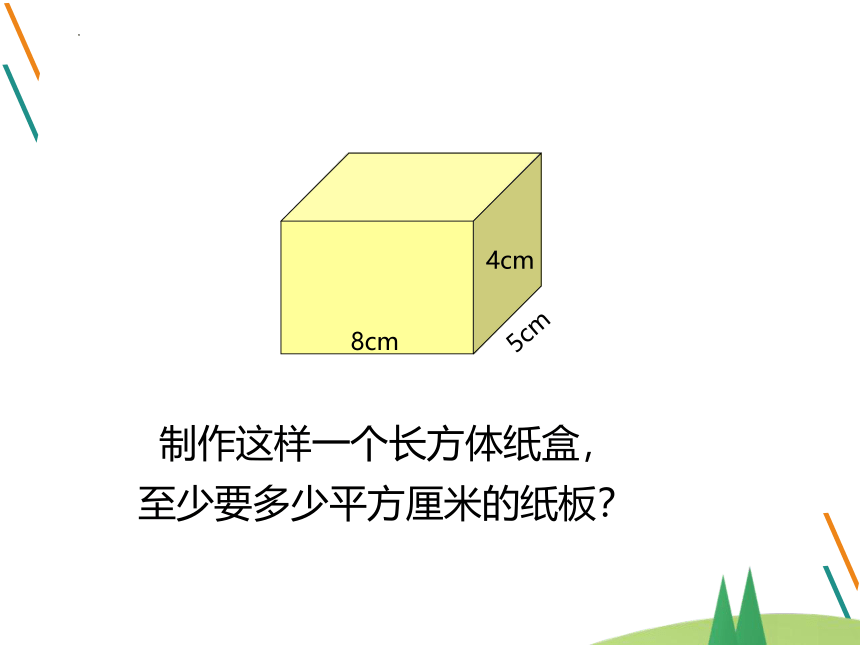
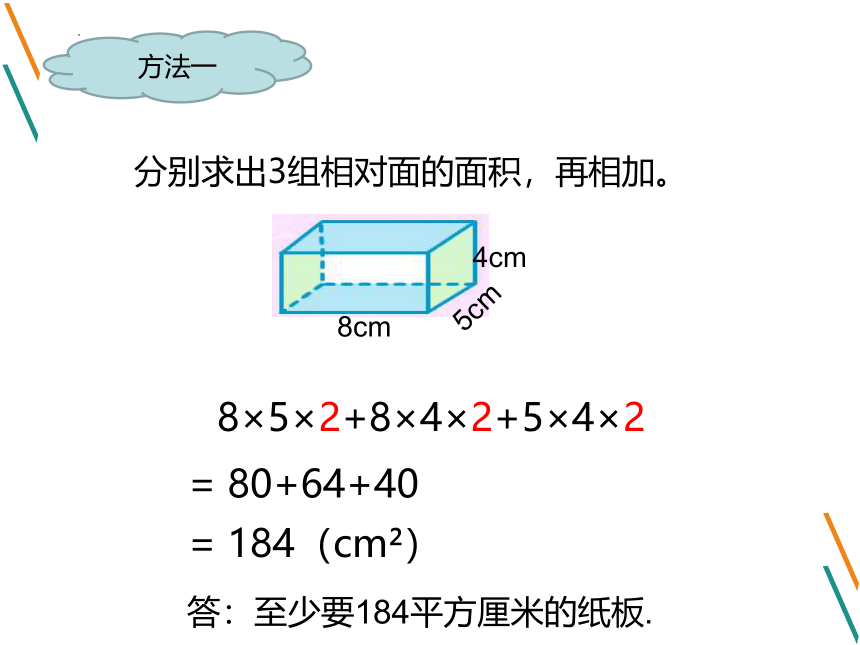
4cm
5cm
8cm
制作这样一个长方体纸盒,
至少要多少平方厘米的纸板?
8×5×2+8×4×2+5×4×2
= 80+64+40
= 184(cm )
分别求出3组相对面的面积,再相加。
方法一
8cm
5cm
4cm
答:至少要184平方厘米的纸板.
(8×5+8×4+5×4)×2
= (40+32+20)×2
= 92×2
= 184(cm )
先求出每组相对的面中一个面的面积,相加再乘2。
方法二
8cm
5cm
4cm
答:至少要184平方厘米的纸板.
长
宽
高
长方体的表面积=长×宽×2+长×高×2+宽×高×2
长方体的表面积=(长×宽+长×高+宽×高)×2
一个棱长为2cm的正方体的表面积是多少?
2cm
2×2×6
= 4×6
= 24(cm )
先求出一个面的面积,再乘6。
2cm
答:它的表面积是24 cm2 。
正方体的展开图
棱
正方体每个面都是正方形。
正方体的表面积 = 棱长×棱长×6
做一个长是25cm,宽是10cm,高是35cm这样的手提纸袋,至少需要多少平方厘米的纸?
25×35×2+10×35×2+25×10
= 1750+700+250
= 2700(cm2)
答:至少需要2700cm2的纸。
还可以怎样算?
课堂探索
(25×35+10×35+10×25)×2
= (875+350+250)×2
=1475×2
= 2950(cm2)
2950-10×25
=2950-250
=2700(cm2)
答:至少需要2700cm2的纸。
还可以这样算
在解决与长方体、正方体表面积有关的实际问题时,应当注意些什么?
课堂练习一
这些问题分别要求长方体哪几个面的面积?
(1)长方体通风管道的用料面积。
(2)长方体水池内铺瓷砖的面积。
(3)教室内粉刷墙面的面积。
(4)长方体油桶的用料面积。
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
(1)猜一猜它们的表面积是否相等。摆一摆,算一算。
课堂练习二
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
(1)猜一猜它们的表面积是否相等。摆一摆,算一算。
方法一
方法二
方法三
长8cm
高1cm
宽1cm
(8×1+8×1+1×1)×2
=17×2
=34 (c㎡)
(1)猜一猜它们的表面积是否相等。
(1)上、下两个面的面积的和是( )。
(1)猜一猜它们的表面积是否相等。
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
长方体或正方体6个面的面积之和是它的表面积。
长方体或正方体6个面的面积之和是它的表面积。
(4×1+1×2+4×2)×2
正方体的表面积=棱长 ×棱长× 6
8×5×2+5×4×2+8×4×2
一个物体表面所有面的面积之和叫做它的表面积
(4×1+1×2+4×2)×2
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
计算这个长方体的表面积。
(1)上、下两个面的面积的和是( )。
(2)前、后两个面的面积的和是( )。
(4×5+4×3.
(2)表面积的大小与摆成的形状有关系吗?
(1)猜一猜它们的表面积是否相等。
(1)猜一猜它们的表面积是否相等。
正方体的6个面都相等。
长4cm
高1cm
宽2cm
(4×2+4×1+1×2)×2
=14×2
=28 (c㎡)
棱长2cm
2×2×6
=4×6
=24 (c㎡)
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
(1)猜一猜它们的表面积是否相等。摆一摆,算一算。
(2)表面积的大小与摆成的形状有关系吗?
课堂练习二
通过这节课的学习,你学到了什么?
课堂总结
课堂总结
长方体或正方体6个面的面积之和,叫做它的表面积。
长方体的表面积=(长×宽 + 长×高 + 宽×高)×2
正方体的表面积 =棱长×棱长×6
谢谢大家。
西师版五年级下册第三单元
长方体、正方体的表面积
你知道自己的生日是哪一天吗?你最想收到什么生日礼物呢?
下面这些立体图形的表面是由几个面组成的?每个面各是什么形状?
长方体或正方体露在外面的部分,也就是这6个面,我们称为长方体或正方体的表面。
用剪刀沿着棱分别剪开长方体和正方体盒子,观察展开后的效果。
前
上
右
前
上
右
前
右
下
后
上
左
前
右
下
后
上
左
展开后的一种效果。
表面所有面的面积之和就是它的表面积 。
长方体或正方体6个面的面积之和,就是它的表面积。
4cm
5cm
8cm
制作这样一个长方体纸盒,
至少要多少平方厘米的纸板?
8×5×2+8×4×2+5×4×2
= 80+64+40
= 184(cm )
分别求出3组相对面的面积,再相加。
方法一
8cm
5cm
4cm
答:至少要184平方厘米的纸板.
(8×5+8×4+5×4)×2
= (40+32+20)×2
= 92×2
= 184(cm )
先求出每组相对的面中一个面的面积,相加再乘2。
方法二
8cm
5cm
4cm
答:至少要184平方厘米的纸板.
长
宽
高
长方体的表面积=长×宽×2+长×高×2+宽×高×2
长方体的表面积=(长×宽+长×高+宽×高)×2
一个棱长为2cm的正方体的表面积是多少?
2cm
2×2×6
= 4×6
= 24(cm )
先求出一个面的面积,再乘6。
2cm
答:它的表面积是24 cm2 。
正方体的展开图
棱
正方体每个面都是正方形。
正方体的表面积 = 棱长×棱长×6
做一个长是25cm,宽是10cm,高是35cm这样的手提纸袋,至少需要多少平方厘米的纸?
25×35×2+10×35×2+25×10
= 1750+700+250
= 2700(cm2)
答:至少需要2700cm2的纸。
还可以怎样算?
课堂探索
(25×35+10×35+10×25)×2
= (875+350+250)×2
=1475×2
= 2950(cm2)
2950-10×25
=2950-250
=2700(cm2)
答:至少需要2700cm2的纸。
还可以这样算
在解决与长方体、正方体表面积有关的实际问题时,应当注意些什么?
课堂练习一
这些问题分别要求长方体哪几个面的面积?
(1)长方体通风管道的用料面积。
(2)长方体水池内铺瓷砖的面积。
(3)教室内粉刷墙面的面积。
(4)长方体油桶的用料面积。
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
(1)猜一猜它们的表面积是否相等。摆一摆,算一算。
课堂练习二
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
(1)猜一猜它们的表面积是否相等。摆一摆,算一算。
方法一
方法二
方法三
长8cm
高1cm
宽1cm
(8×1+8×1+1×1)×2
=17×2
=34 (c㎡)
(1)猜一猜它们的表面积是否相等。
(1)上、下两个面的面积的和是( )。
(1)猜一猜它们的表面积是否相等。
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
长方体或正方体6个面的面积之和是它的表面积。
长方体或正方体6个面的面积之和是它的表面积。
(4×1+1×2+4×2)×2
正方体的表面积=棱长 ×棱长× 6
8×5×2+5×4×2+8×4×2
一个物体表面所有面的面积之和叫做它的表面积
(4×1+1×2+4×2)×2
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
计算这个长方体的表面积。
(1)上、下两个面的面积的和是( )。
(2)前、后两个面的面积的和是( )。
(4×5+4×3.
(2)表面积的大小与摆成的形状有关系吗?
(1)猜一猜它们的表面积是否相等。
(1)猜一猜它们的表面积是否相等。
正方体的6个面都相等。
长4cm
高1cm
宽2cm
(4×2+4×1+1×2)×2
=14×2
=28 (c㎡)
棱长2cm
2×2×6
=4×6
=24 (c㎡)
用8个棱长1cm的小正方体摆成不同形状的长方体或正方体。
(1)猜一猜它们的表面积是否相等。摆一摆,算一算。
(2)表面积的大小与摆成的形状有关系吗?
课堂练习二
通过这节课的学习,你学到了什么?
课堂总结
课堂总结
长方体或正方体6个面的面积之和,叫做它的表面积。
长方体的表面积=(长×宽 + 长×高 + 宽×高)×2
正方体的表面积 =棱长×棱长×6
谢谢大家。
