北京版八年级数学下册《17.1 方差》教学设计(表格式)
文档属性
| 名称 | 北京版八年级数学下册《17.1 方差》教学设计(表格式) |  | |
| 格式 | doc | ||
| 文件大小 | 248.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 12:17:19 | ||
图片预览


文档简介
一、教学基本信息
年级 七年级 学期 第2学期
教材 北京课改版 学生人数
授课课题 方差 课型 新授课
二、教学背景分析
《义务教育数学课程标准》对本节内容的教学要求是:体会刻画数据离散程度的意义,会计算简单数据的方差。教学建议是:“在统计教学中,设计有效的统计活动,使学生经历完整的统计过程,不断积累统计活动经验,加深理解统计思想与方法。”教材分析:本节内容属于“统计与概率”领域的统计部分,是统计中常用的一种刻画数据离散程度的统计量。本节课选自北京出版社义务教育教科书数学八年级下册第17章第一节《方差》的第1课时,它是在研究了平均数、中位数、众数这些统计量(用来分析数据的集中趋势的量)之后,进一步研究另外一种统计的方法——方差。 “方差”属于数学中的统计与概率范畴,它的特点是与生活中的实际问题联系紧密,是刻画数据离散程度的统计量,对学生统计观念的形成有着举足轻重的作用,这些知识的储备与技能的训练为本节课的学习打好了基础。学情分析:八年级学生思维活跃,各种基本智力因素(言语、感知、记、想象、思维)得到进一步提高和完善,能逐渐运用假设,抽象概念,逻辑法则以及逻辑推理手段提高解决问题的能力,使他们能更轻松,更快捷,更有效的完成各种认知任务。学生已经掌握计算数据的平均数、加权平均数、众数和中位数的方法,会用学过的统计量分析数据。通过前测调研,学生对于平均数,众数的理解和掌握较好,中位数较差。对于分析统计量的经验和方法还有待进一步培养,本节课在此基础上,引导学生理解方差的意义,探究方差如何刻画数据的波动情况。
三、教学目标(含重、难点)
一.教学目标【知识与技能】 (1)理解方差的意义,掌握如何刻画一组数据的波动大小。 ( 2)掌握方差的计算公式,初步运用方差解决实际问题。【过程与方法】经历画图、观察,探索如何表示一组数据的离散程度,培养学生分析问题,解决问题的能力,发展合情推理,发展统计观念和应用意识。【情感态度价值观】经历探索如何表示一组数据的离散程度,感受数学来源于实践,又作用于实践,感知数学知识的抽象美,提高参与数学学习的积极性。 二.教学重点:方差的意义,对数据波动大小规律的理解。三.教学难点:方差意义的理解及方差计算公式的得出。
四、教学过程
教学步骤 教师活动 学生活动 设计意图
一.开门见山,引入新课. 我校社团活动丰富多彩,曲棍球队在市级,全国乃至国外的比赛中,都取得了优异成绩,有李凯,高雷两名队员被选拔到国家少年男子曲棍球队。我校的射箭队经过两年的训练,成绩也是突飞猛进,市级队教练来到我校,对两名学生进行选拔,我们一起来看他们的训练成绩。 学生倾听 从我校实际生活中的问题入手,激发学生的学习兴趣,引发学生积极思考,寻找解决问题的方法。
二.解决问题,学习新知. 第一步:平均数、中位数、众数、极差.甲,乙两名射箭手的测试成绩统计如下:若你是教练,你会如何选拔为什么? 第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068第二步:探索方差1. 如何表示出他们成绩的稳定程度?我们可以在平面直角坐标系中通过描点画图观察甲乙两人各自的射箭情况。2.观察甲乙两组数据中每个数据偏离平均数的情况?3.怎样消除防止正偏差与负偏差的相互抵消的情况?第三步:得出方差的计算方法先求平均数,后求差的平方和,再求平均数第四步:体会方差的作用 生1:看他们的平均水平(平均数)生2:预案1.众数,中位数 预案2.比较他们的稳定程度1.通过观察折线图直接感知甲的波动小,乙的波动大2.计算两组数据偏离平均数的平均距离方差越大,说明数据的波动越大,数据越不稳定;方差越小,说明数据的波动越小,数据越稳定。 运用旧知解决问题,引发认知冲突。本阶段的教学是本节课的重点也是难点,学生不易理解为什么要用方差去描述一组数据的波动大小,为什么不可以用各数据与其平均数的差的和来衡量这组数据的波动大小呢?(消除正偏差,负偏差相互抵消的情况)为什么对各数据与其平均数的差不取其绝对值,而将其平方呢?(绝对值使用不便,统计中很少应用)
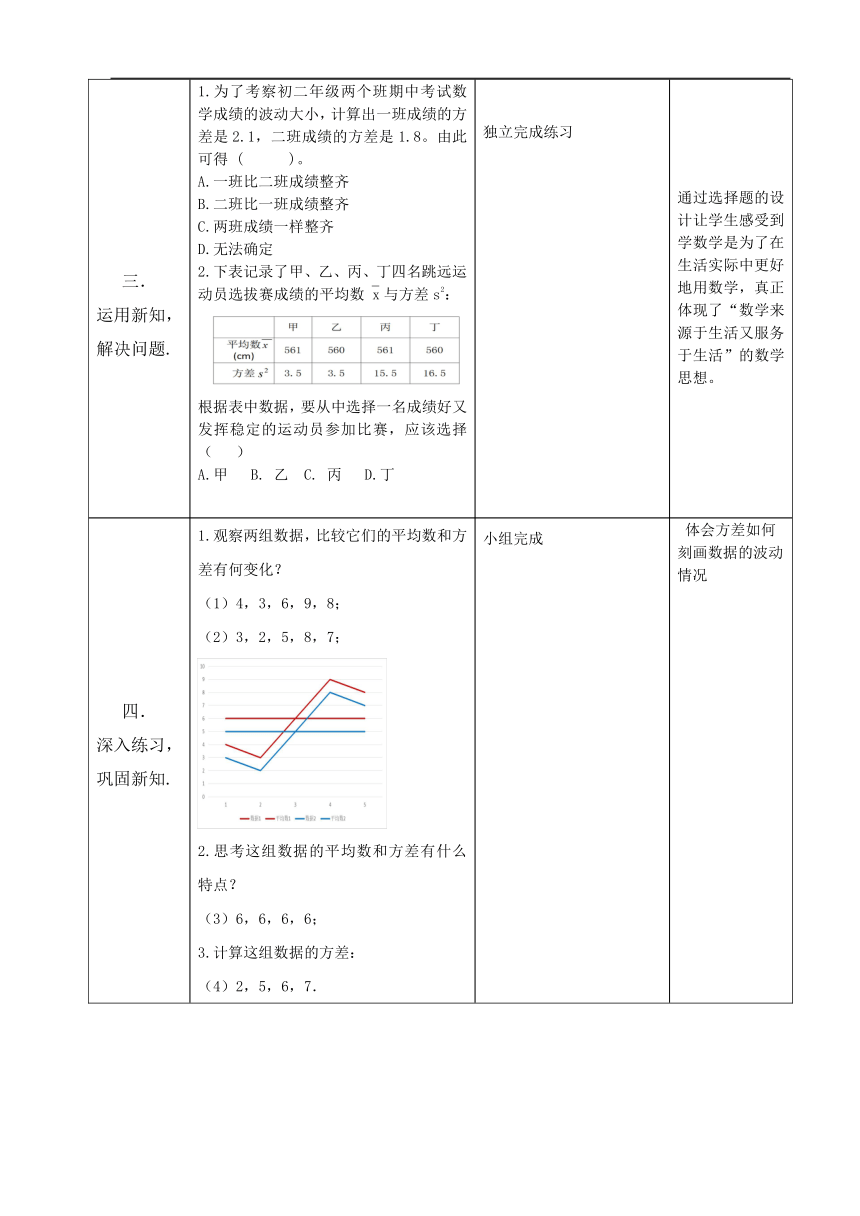
三.运用新知,解决问题. 1.为了考察初二年级两个班期中考试数学成绩的波动大小,计算出一班成绩的方差是2.1,二班成绩的方差是1.8。由此可得 ( )。 A.一班比二班成绩整齐B.二班比一班成绩整齐 C.两班成绩一样整齐 D.无法确定 2.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x与方差s2: 根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )A.甲 B. 乙 C. 丙 D.丁 独立完成练习 通过选择题的设计让学生感受到学数学是为了在生活实际中更好地用数学,真正体现了“数学来源于生活又服务于生活”的数学思想。
四.深入练习,巩固新知. 1.观察两组数据,比较它们的平均数和方差有何变化?(1)4,3,6,9,8;(2)3,2,5,8,7;2.思考这组数据的平均数和方差有什么特点? (3)6,6,6,6;3.计算这组数据的方差:(4)2,5,6,7. 小组完成 体会方差如何刻画数据的波动情况
五.课堂小结,布置作业. 知识小结:通过这节课的学习,我们更深刻的认识了数据,平均数,中位数是来比较两组数据集中趋势的统计量,在集中趋势相同或相近时,就要比较离散程度,即波动的大小。极差刻画是数据的波动范围,方差刻画的是数据波动的大小。方法小结:求一组数据方差的方法;先求平均数,再利用方差公式求方差。 倾听教师总结,内心体验本节课的收获 体会知识间的联系与区别,更深入的理解方差的意义。
五、板书设计
数据的波动——方差极差:刻画数据波动的范围甲:[(7-8)+(8-8)+(8-8)+(8-8)+(9-8)]=0乙: [(10-8)+(6-8)+(10-8)+(6-8)+(8-8)]=0甲:s2=[(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2]=乙:s2= [(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2]=方差:刻画数据波动的大小
《数据的波动——方差》学案
一.例题
甲,乙两名射击手的测试成绩统计如下:若你是教练,你认为挑选哪一位
比较适宜?为什么?
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
乙命中环数 10 6 10 6 8
二.练习
1. 为了考察初二年级两个班期中考试数学成绩的波动大小,计算出一班成绩的
方差是2.1,二班成绩的方差是1.8。由此可得 ( )。
A.一班比二班成绩整齐 B.二班比一班成绩整齐
C.两班成绩一样整齐 D.无法确定
2.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x与方差s2:
根据表中数据,选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B. 乙 C. 丙 D.丁
三.提升
1.观察两组数据,比较它们的平均数和方差有何变化?
(1)4,3,6,9,8;
(2)3,2,5,8,7;
2.思考这组数据的平均数和方差有什么特点?
(3)6,6,6,6;
3.计算这组数据的方差:
(4)2,5,6,7.
备用1 备用2 备用3
PAGE
年级 七年级 学期 第2学期
教材 北京课改版 学生人数
授课课题 方差 课型 新授课
二、教学背景分析
《义务教育数学课程标准》对本节内容的教学要求是:体会刻画数据离散程度的意义,会计算简单数据的方差。教学建议是:“在统计教学中,设计有效的统计活动,使学生经历完整的统计过程,不断积累统计活动经验,加深理解统计思想与方法。”教材分析:本节内容属于“统计与概率”领域的统计部分,是统计中常用的一种刻画数据离散程度的统计量。本节课选自北京出版社义务教育教科书数学八年级下册第17章第一节《方差》的第1课时,它是在研究了平均数、中位数、众数这些统计量(用来分析数据的集中趋势的量)之后,进一步研究另外一种统计的方法——方差。 “方差”属于数学中的统计与概率范畴,它的特点是与生活中的实际问题联系紧密,是刻画数据离散程度的统计量,对学生统计观念的形成有着举足轻重的作用,这些知识的储备与技能的训练为本节课的学习打好了基础。学情分析:八年级学生思维活跃,各种基本智力因素(言语、感知、记、想象、思维)得到进一步提高和完善,能逐渐运用假设,抽象概念,逻辑法则以及逻辑推理手段提高解决问题的能力,使他们能更轻松,更快捷,更有效的完成各种认知任务。学生已经掌握计算数据的平均数、加权平均数、众数和中位数的方法,会用学过的统计量分析数据。通过前测调研,学生对于平均数,众数的理解和掌握较好,中位数较差。对于分析统计量的经验和方法还有待进一步培养,本节课在此基础上,引导学生理解方差的意义,探究方差如何刻画数据的波动情况。
三、教学目标(含重、难点)
一.教学目标【知识与技能】 (1)理解方差的意义,掌握如何刻画一组数据的波动大小。 ( 2)掌握方差的计算公式,初步运用方差解决实际问题。【过程与方法】经历画图、观察,探索如何表示一组数据的离散程度,培养学生分析问题,解决问题的能力,发展合情推理,发展统计观念和应用意识。【情感态度价值观】经历探索如何表示一组数据的离散程度,感受数学来源于实践,又作用于实践,感知数学知识的抽象美,提高参与数学学习的积极性。 二.教学重点:方差的意义,对数据波动大小规律的理解。三.教学难点:方差意义的理解及方差计算公式的得出。
四、教学过程
教学步骤 教师活动 学生活动 设计意图
一.开门见山,引入新课. 我校社团活动丰富多彩,曲棍球队在市级,全国乃至国外的比赛中,都取得了优异成绩,有李凯,高雷两名队员被选拔到国家少年男子曲棍球队。我校的射箭队经过两年的训练,成绩也是突飞猛进,市级队教练来到我校,对两名学生进行选拔,我们一起来看他们的训练成绩。 学生倾听 从我校实际生活中的问题入手,激发学生的学习兴趣,引发学生积极思考,寻找解决问题的方法。
二.解决问题,学习新知. 第一步:平均数、中位数、众数、极差.甲,乙两名射箭手的测试成绩统计如下:若你是教练,你会如何选拔为什么? 第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068第二步:探索方差1. 如何表示出他们成绩的稳定程度?我们可以在平面直角坐标系中通过描点画图观察甲乙两人各自的射箭情况。2.观察甲乙两组数据中每个数据偏离平均数的情况?3.怎样消除防止正偏差与负偏差的相互抵消的情况?第三步:得出方差的计算方法先求平均数,后求差的平方和,再求平均数第四步:体会方差的作用 生1:看他们的平均水平(平均数)生2:预案1.众数,中位数 预案2.比较他们的稳定程度1.通过观察折线图直接感知甲的波动小,乙的波动大2.计算两组数据偏离平均数的平均距离方差越大,说明数据的波动越大,数据越不稳定;方差越小,说明数据的波动越小,数据越稳定。 运用旧知解决问题,引发认知冲突。本阶段的教学是本节课的重点也是难点,学生不易理解为什么要用方差去描述一组数据的波动大小,为什么不可以用各数据与其平均数的差的和来衡量这组数据的波动大小呢?(消除正偏差,负偏差相互抵消的情况)为什么对各数据与其平均数的差不取其绝对值,而将其平方呢?(绝对值使用不便,统计中很少应用)
三.运用新知,解决问题. 1.为了考察初二年级两个班期中考试数学成绩的波动大小,计算出一班成绩的方差是2.1,二班成绩的方差是1.8。由此可得 ( )。 A.一班比二班成绩整齐B.二班比一班成绩整齐 C.两班成绩一样整齐 D.无法确定 2.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x与方差s2: 根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )A.甲 B. 乙 C. 丙 D.丁 独立完成练习 通过选择题的设计让学生感受到学数学是为了在生活实际中更好地用数学,真正体现了“数学来源于生活又服务于生活”的数学思想。
四.深入练习,巩固新知. 1.观察两组数据,比较它们的平均数和方差有何变化?(1)4,3,6,9,8;(2)3,2,5,8,7;2.思考这组数据的平均数和方差有什么特点? (3)6,6,6,6;3.计算这组数据的方差:(4)2,5,6,7. 小组完成 体会方差如何刻画数据的波动情况
五.课堂小结,布置作业. 知识小结:通过这节课的学习,我们更深刻的认识了数据,平均数,中位数是来比较两组数据集中趋势的统计量,在集中趋势相同或相近时,就要比较离散程度,即波动的大小。极差刻画是数据的波动范围,方差刻画的是数据波动的大小。方法小结:求一组数据方差的方法;先求平均数,再利用方差公式求方差。 倾听教师总结,内心体验本节课的收获 体会知识间的联系与区别,更深入的理解方差的意义。
五、板书设计
数据的波动——方差极差:刻画数据波动的范围甲:[(7-8)+(8-8)+(8-8)+(8-8)+(9-8)]=0乙: [(10-8)+(6-8)+(10-8)+(6-8)+(8-8)]=0甲:s2=[(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2]=乙:s2= [(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2]=方差:刻画数据波动的大小
《数据的波动——方差》学案
一.例题
甲,乙两名射击手的测试成绩统计如下:若你是教练,你认为挑选哪一位
比较适宜?为什么?
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
乙命中环数 10 6 10 6 8
二.练习
1. 为了考察初二年级两个班期中考试数学成绩的波动大小,计算出一班成绩的
方差是2.1,二班成绩的方差是1.8。由此可得 ( )。
A.一班比二班成绩整齐 B.二班比一班成绩整齐
C.两班成绩一样整齐 D.无法确定
2.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x与方差s2:
根据表中数据,选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲 B. 乙 C. 丙 D.丁
三.提升
1.观察两组数据,比较它们的平均数和方差有何变化?
(1)4,3,6,9,8;
(2)3,2,5,8,7;
2.思考这组数据的平均数和方差有什么特点?
(3)6,6,6,6;
3.计算这组数据的方差:
(4)2,5,6,7.
备用1 备用2 备用3
PAGE
同课章节目录
