多项式乘以多项式

课件26张PPT。11.4 整式的乘法（3）多项式乘以多项式 如何进行单项式乘单项式的运算？ 单×单
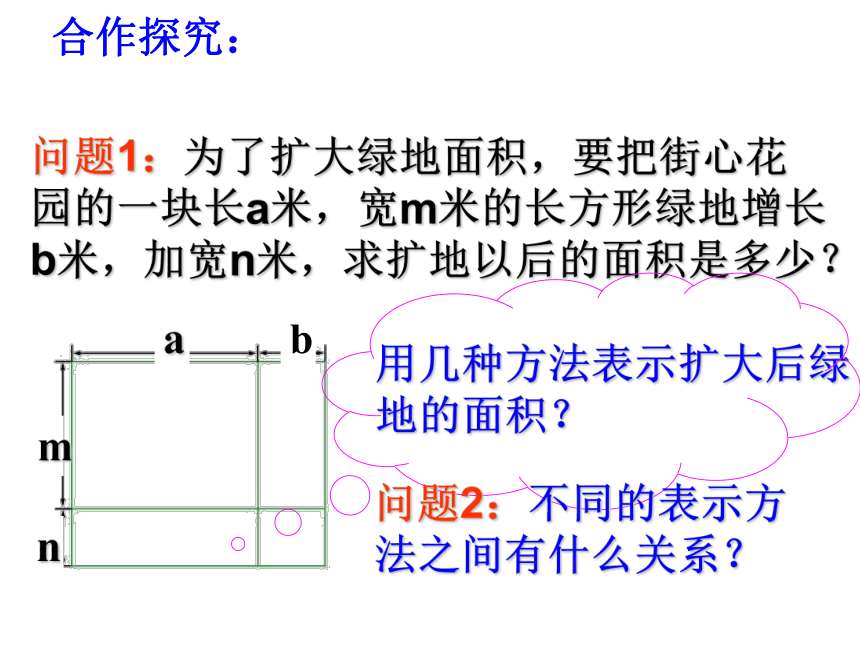
＝(系数×系数)(同底数幂×同底数幂)(单独的幂) 如何进行单项式乘多项式的运算？ 单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.=问题1：为了扩大绿地面积，要把街心花园的一块长a米，宽m米的长方形绿地增长b米，加宽n米，求扩地以后的面积是多少？合作探究：问题2：不同的表示方法之间有什么关系？
方法四：这块花园是由上两块和下两块组成 面积为 m(a+b)+n(a+b)米2.方法三：这块花园是由前两块和后两块组成 面积为 a(m+n)+b(m+n)米2方法二：这块花园现在是由四小块组成，它们的面积分别为：am米2、an米2、bm米2、bn米2，故这块绿地的面积为(am+an+bm+bn)米2．方法一：这块花园现在长(a+b)米，宽(m+n)米，因而面积为(a+b)(m+n)米2． ∵这四种方法表示同一块绿地的面积，∴(a+b)(m+n)=am+an+bm+bn
合作探究：问题2：上面的问题，我们从面积的角度得出了一些等式，下面你能不能尝试从代数运算的角度解释等式的合理性. =am+an+bm+bn 或∴ (a+b)(m+n)=a(m+n)+b(m+n)
=am+an+bm+bn
(a+b)(m+n)=m(a+b)+n(a+b)新知探究：(a+b)(m+n)=am+an+bm+bn(a+b)(m+n)=a(m+n)+b(m+n) ----单×多=am+an+bm+bn ----单×单总体上看，(a+b)(m+n)的结果可以看作由a+b得每一项乘m+n的每一项，再把所得的积相加而得到，即
(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则：(a+b)(m+n)=am1234+an+bm+bn拓展： (a+b+c)(m+n)
=am+an+bm+bn+cm+cn问题4：未合并同类项之前多项式与多项式的积
的项数等于两个多项式的项数之积吗？例题解析 【例1】计算： (1)(x+2)(x?3), (2)(3x -1)(2x+1)。?3x+2x=x2 -x-6 -2×3（2） (3x -1)(2x+1)=3x?2x+3x? 1-1?2 x?1=6x2+3x-2 x?1=6x2 +x?1. 【例2】计算： (1)(x?3y)(x+7y), (2)(2x + 5y)(3x?2y)。+7xy?3yx-=x2 +4xy-21y2； 21y2（2） (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x?5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.1、2、3、巩固新知练习 计算：(1) (2a–3b)(a+5b) ;(2) (xy–z)(2xy+z) ;(3) (x–1)(x2+x+1) ;(4) (2a+b)2;(5) (3a–2)(a–1)–(a+1)(a+2) ;(6) (x+y)(2x–y)(3x+2y).注 意 !1.计算(2a+b)2应该这样做：
(2a+b)2=(2a+b)(2a+b)
=4a2+2ab+2ab+b2
=4a2+4ab+b2
切记 一般情况下
(2a+b)2不等于4a2+b2 .注 意 !2.(3a–2)(a–1)–(a+1)(a+2)是多项式的积与积的差，后两个多项式乘积的展开式要用括号括起来。
3. (x+y)(2x–y)(3x+2y)是三个多项式相乘，应该选其中的两个先相乘，把它们的积用括号括起来，再与第三个相乘。 注意：
1、必须做到不重复，不遗漏2、注意确定积中每一项的符号
3、结果应化为最简式
需要注意的几个问题 计算：
(1) ( 3x -1 )( x +2 ) ;
(2) ( x – 3y )( x – y )
(3) (x+y)(x2-xy+y2)
练习:
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ； (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3) (x+2)(x+3) = x2 + 5x+6
(x – 4)(x+1) = x2 –3x – 4
(y+4)(y – 2) = y2 + 2y – 8
(y – 5)(y – 3) = y2 – 8y+15
观察上述式子，你可以 得出一个什么规律吗？ (x+p)(x+q) = x2 + (p+q) x + p q
确定下列各式中m与p的值:
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x2 + m x + 36
(3) (x+3)(x+p) = x2 + m x + 36
(4) (x-6) (x-p) = x2 + m x + 36
(5) (x+p)(x+q) = x2 + m x + 36
(1) m =13 (2) m = - 20 (3) p =12, m= 15(4) p= 6, m= -12(5) p = 4,q = 9, m =13 p=2,q = 18, m=20 p = 3, q =12, m=15 p=6, q= 6, m=12拓展与应用 (x+p)(x+q) = x2 + (p+q) x + p q(p，q为正整数)…………根据上述结论计算：
(1) (x+1)(x+2)=
(2) (x+1)(x-2)=
(3) (x-1)(x+2)=
(4) (x-1)(x-2)=x2+3x+2x2-x-2x2+x-2x2-3x+2 (x+p)(x+q) = x2 + (p+q) x + p q拓展与应用5、观察下列各式：
(x-1)(x2+x+1)=x3-1
(2a+b)(4a2-2ab+b2)=8a3+b3
(m-3n)(m2+3mn+9n2)=m3-27n3
（1）请你用字母表示出上述计算的规律；
（2）利用上面的规律计算：
拓展提高归纳小结谈谈你这节课的收获！！你讲我说共交流多项式乘以多项式法则： 1.多项式与多项式相乘，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加。 注意：
1、必须做到不重复，不遗漏；2、注意确定积中每一项的符号；
3、最后结果应合并同类项。
4、观察下列各式：
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
……
根据前面各式的规律可得到：
(x-1)(xn+xn-1+xn-2+……+x+1)=________拓展提高Xn+1-1中考链接:(1) (2011年 宁夏)
已知：a+b=3/2 ,ab=1 化简(a-2)(b-2)的结果是（ ）
（2） (2011年 北京)已知 ：x2-5x=14 求：
(x-1)(2x-1)-(x+1) 2+1的值
解：原式=2x2-3x+1-(x2+2x+1)+1
=2x2-3x+1-x2-2x-1+1
=x2-5x+1
将x2-5x=14代入原式 =14+1=15。2能力挑战