人教版六年级上学期数学第五单元5.5整理和复习 课件(共18张PPT)
文档属性
| 名称 | 人教版六年级上学期数学第五单元5.5整理和复习 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 08:07:41 | ||
图片预览




文档简介
(共18张PPT)
整理与复习
使学生能正确运用圆的有关知识,解决简单的实际问题。
使学生进一步体会运用已有知识解决新问题的乐趣,发展空间观念和初步的推理能力。
了解现实生活中有许多与圆的面积有关的问题,获得运用知识解决问题的成功体验。
圆的面积和圆环的面积计算
“外圆内方,外方内圆”图形面积的计算
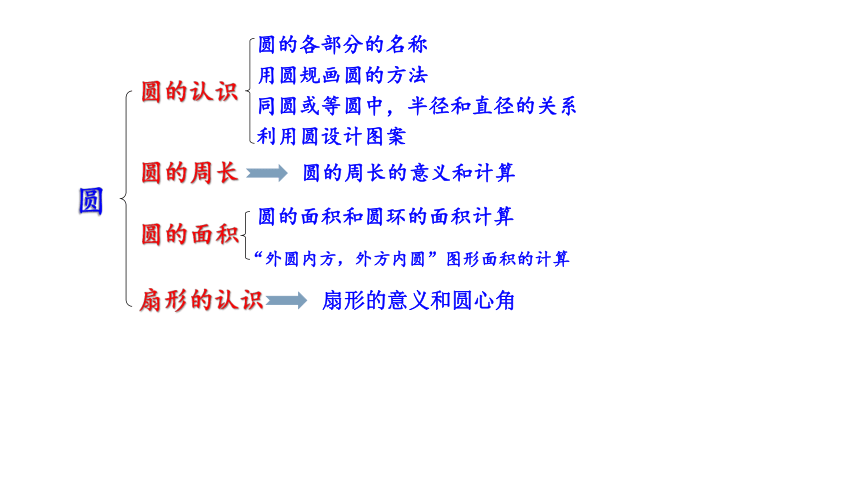
圆
圆的认识
扇形的认识
圆的各部分的名称
用圆规画圆的方法
同圆或等圆中,半径和直径的关系
利用圆设计图案
圆的周长
圆的面积
圆的周长的意义和计算
扇形的意义和圆心角
圆的周长
周长与直径的比值,叫做圆周率。用公式表示:
圆的周长公式:
半圆的周长:
已知周长求直径:
2
圆的面积
1.圆所占平面的大小,叫做圆的面积。
2.圆的面积公式:
r
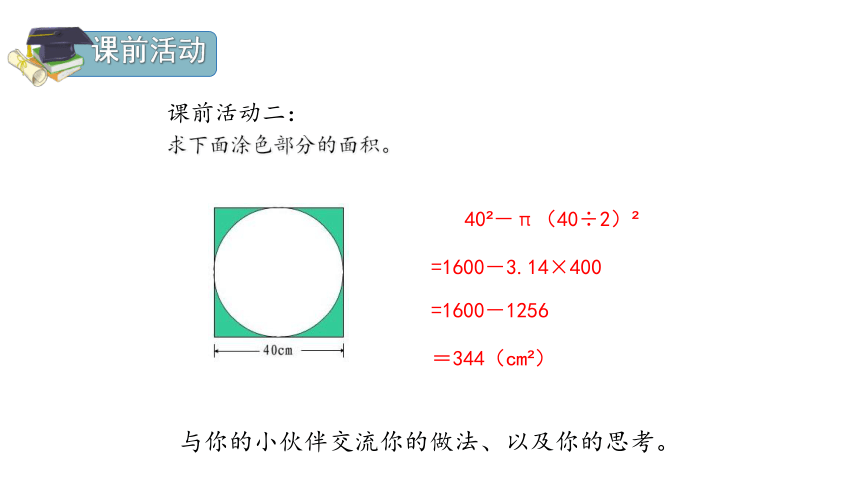
课前活动二:
求下面涂色部分的面积。
40 -π(40÷2)
=1600-3.14×400
=344(cm )
课前活动
与你的小伙伴交流你的做法、以及你的思考。
=1600-1256
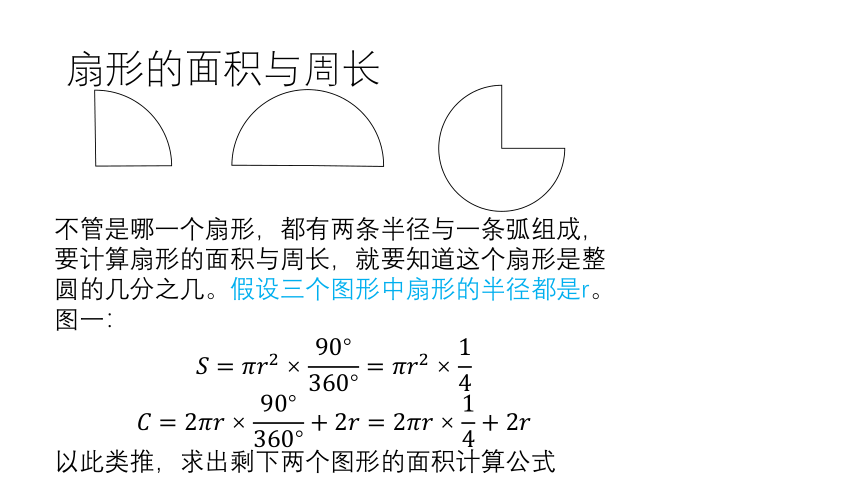
扇形的面积与周长
不管是哪一个扇形,都有两条半径与一条弧组成,要计算扇形的面积与周长,就要知道这个扇形是整圆的几分之几。假设三个图形中扇形的半径都是r。
图一:
以此类推,求出剩下两个图形的面积计算公式
探究二:
可以把正方形看成两个三角形,它的底是圆的直径,高是圆的半径。
=3.14×12-(2×1÷2)×2
=3.14-2
=1.14(平方米)
扇形的认识
1.一条弧和经过这条弧两端的半径所围成的图形叫做扇形。
2.在同圆或者等圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
1.右图中的铜钱直径28毫米,中间的正方形边长为6毫米。这个铜钱的面积是多少?
答:这个铜钱的面积是579.44mm 。
3.14×(28÷2) -6
=615.44-36
=579.44(mm )
(3)如果在这张餐桌的中央放一个半径是0.5 m的圆形转盘,剩下的桌面的面积是多少?
S圆环=π(R2-r2)
=3.14×(12-0.52)
=2.355(m2)
答:剩下的桌面的面积是2.355m2。
外圆半径为:2÷2=1(m)
圆的应用
一个圆滚动一周,相当于前进了这个圆的周长的距离。
在一个圆上等距离的描点,描了多少个点,就把圆分成了几份。
面积:100×(32×2)+3.14×322
=6400+3215.36
=9615.36(m2)
3.一个运动场如右图,两端是半圆形,中间是长方形,这个运动场的周长是多少米?面积是多少米?
答:这个运动场的面积是9615.36m2。
5.用10 m长的铁条做直径是50 cm的圆形铁环,最多可以做多少个?
(教材P78“练习十七”第3题)
铁条长度为:10 m=1000 cm
【分析】
求可以做多少个圆形铁环,就是求10m长的铁条是圆形铁环周长的多少倍。
圆形铁环的周长C=πd=3.14×50=157(cm)
1000÷157≈6(个)
答:最多可以做6个。
圆的应用
如果有几个圆(或者半圆弧)的直径之和,等于另外一个圆(半圆弧)的直径,那么这几个圆(半圆弧)的周长也等于这个大圆的周长
假设三个小圆的直径分
别是,你
能不能验证这个结论?
先算算各个圆形的周长,
再把图形的下半部分盖住,
计算一下几个半圆的周长。。
1.完成《解决生活中圆的问题课后作业》;
2.讨论交流:
观看微课《扇形、圆心角和弧》,举例说说你对扇形的认识,归纳总结后,交流互评。
作业布置
Goodbye~
感谢聆听,下期再会
整理与复习
使学生能正确运用圆的有关知识,解决简单的实际问题。
使学生进一步体会运用已有知识解决新问题的乐趣,发展空间观念和初步的推理能力。
了解现实生活中有许多与圆的面积有关的问题,获得运用知识解决问题的成功体验。
圆的面积和圆环的面积计算
“外圆内方,外方内圆”图形面积的计算
圆
圆的认识
扇形的认识
圆的各部分的名称
用圆规画圆的方法
同圆或等圆中,半径和直径的关系
利用圆设计图案
圆的周长
圆的面积
圆的周长的意义和计算
扇形的意义和圆心角
圆的周长
周长与直径的比值,叫做圆周率。用公式表示:
圆的周长公式:
半圆的周长:
已知周长求直径:
2
圆的面积
1.圆所占平面的大小,叫做圆的面积。
2.圆的面积公式:
r
课前活动二:
求下面涂色部分的面积。
40 -π(40÷2)
=1600-3.14×400
=344(cm )
课前活动
与你的小伙伴交流你的做法、以及你的思考。
=1600-1256
扇形的面积与周长
不管是哪一个扇形,都有两条半径与一条弧组成,要计算扇形的面积与周长,就要知道这个扇形是整圆的几分之几。假设三个图形中扇形的半径都是r。
图一:
以此类推,求出剩下两个图形的面积计算公式
探究二:
可以把正方形看成两个三角形,它的底是圆的直径,高是圆的半径。
=3.14×12-(2×1÷2)×2
=3.14-2
=1.14(平方米)
扇形的认识
1.一条弧和经过这条弧两端的半径所围成的图形叫做扇形。
2.在同圆或者等圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
1.右图中的铜钱直径28毫米,中间的正方形边长为6毫米。这个铜钱的面积是多少?
答:这个铜钱的面积是579.44mm 。
3.14×(28÷2) -6
=615.44-36
=579.44(mm )
(3)如果在这张餐桌的中央放一个半径是0.5 m的圆形转盘,剩下的桌面的面积是多少?
S圆环=π(R2-r2)
=3.14×(12-0.52)
=2.355(m2)
答:剩下的桌面的面积是2.355m2。
外圆半径为:2÷2=1(m)
圆的应用
一个圆滚动一周,相当于前进了这个圆的周长的距离。
在一个圆上等距离的描点,描了多少个点,就把圆分成了几份。
面积:100×(32×2)+3.14×322
=6400+3215.36
=9615.36(m2)
3.一个运动场如右图,两端是半圆形,中间是长方形,这个运动场的周长是多少米?面积是多少米?
答:这个运动场的面积是9615.36m2。
5.用10 m长的铁条做直径是50 cm的圆形铁环,最多可以做多少个?
(教材P78“练习十七”第3题)
铁条长度为:10 m=1000 cm
【分析】
求可以做多少个圆形铁环,就是求10m长的铁条是圆形铁环周长的多少倍。
圆形铁环的周长C=πd=3.14×50=157(cm)
1000÷157≈6(个)
答:最多可以做6个。
圆的应用
如果有几个圆(或者半圆弧)的直径之和,等于另外一个圆(半圆弧)的直径,那么这几个圆(半圆弧)的周长也等于这个大圆的周长
假设三个小圆的直径分
别是,你
能不能验证这个结论?
先算算各个圆形的周长,
再把图形的下半部分盖住,
计算一下几个半圆的周长。。
1.完成《解决生活中圆的问题课后作业》;
2.讨论交流:
观看微课《扇形、圆心角和弧》,举例说说你对扇形的认识,归纳总结后,交流互评。
作业布置
Goodbye~
感谢聆听,下期再会
