物理人教版(2019)必修第二册8.3动能和动能定理(共16张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.3动能和动能定理(共16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-30 09:13:19 | ||
图片预览





文档简介
(共16张PPT)
8.3
动能和动能定理
定义:物体因为运动而具有的能量称为动能。
奔驰中的汽车
投出的篮球
发射出的火箭
动能的大小与什么因素有关?
类型一:质量为m 的物体在与运动方向相同的恒力F 的作用下发生一段位移l ,速度从v1 增加到v2
类型二:质量为m 的物体在与运动方向相同的恒力F 的作用下,沿粗糙水平面运动了一段位移l ,受到的摩擦力为Ff ,速度从v1 变为v2
思考:
l
F
v2
Ff
F
v1
Ff
W合=Fl-Ff l = -
mv12
1
2
mv22
1
2
F
v1
F
v2
l
WF = Fl = -
mv12
1
2
mv22
1
2
1.定义:物体由于物体运动而具有的能量。
3.单位:焦耳(J) 1J=1kg·m2/s2
2.表达式:
4.标量:遵从代数运算法则,且只有正值。
5.状态量:对应某一时刻或某一位置,动能具有相对性。
动能的表达式
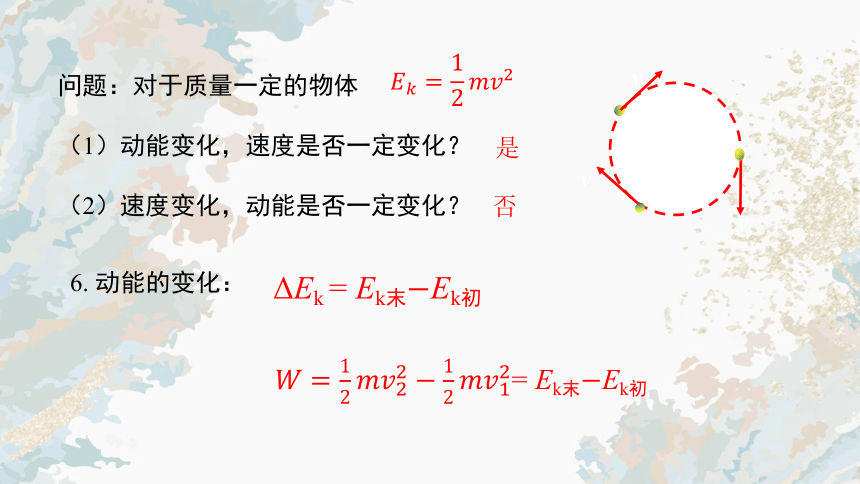
问题:对于质量一定的物体
(1)动能变化,速度是否一定变化?
(2)速度变化,动能是否一定变化?
6. 动能的变化:
v
v
v
否
是
ΔEk = Ek末Ek初
= Ek末Ek初
动能定理
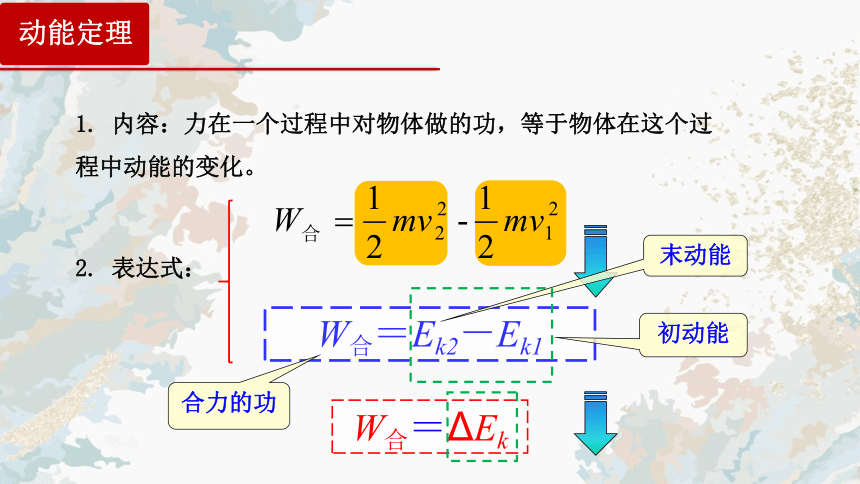
1. 内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化。
W合=Ek2-Ek1
合力的功
末动能
初动能
2. 表达式:
W合=ΔEk
动能定理
(1)合力做正功,即W合>0,Ek2>Ek1 ,动能增大;
(2)合力做负功,即W合<0,Ek2<Ek1 ,动能减小。
4.动能定理的适用范围:
(1)恒力做功或变力做功;
(2)直线运动或曲线运动;
(3)单个物体或多个物体;
(4)一个过程或全过程。
3.对动能定理表达式 的说明:
W合=Ek2-Ek1
例1.一架喷气式飞机,质量 m 为 7.0×104kg,起飞过程中从静止开始滑跑。当位移l达到 2.5×103m 时,速度达到起飞速度 80 m/s。在此过程中,飞机受到的平均阻力是飞机所受重力的 1/50 。g取 10 m/s2,求飞机平均牵引力的大小。
F牵
x
v
F阻
l
O
分析 本题已知飞机滑跑过程的始、末速度,因而能够知道它在滑跑过程中增加的动能。根据动能定理,动能的增加等于牵引力做功和阻力做功的代数和。如图 ,在整个过程中,牵引力对飞机做正功、阻力做负功。由于飞机的位移和所受阻力已知,因而可以求得牵引力的大小
解 以飞机为研究对象, 设飞机滑跑的方向为x轴正方向。飞机的初动能Ek1=0,末动能 ,合力 F 做的功
根据动能定理 ,有
由于
把数值代入后得到
飞机平均牵引力的大小是 1.04×105N。
例2.物体沿高H的光滑斜面从顶端由静止下滑,求它滑到底端时的速度大小.
H
解:由动能定理得 mgH= mv2
∴v=
若物体沿高H的光滑曲面从顶端由静止下滑,结果如何?
仍由动能定理得 mgH= mv2
v=
若由H高处自由下落,结果如何呢?
仍为
v=
例3. 物体在恒定水平推力F的作用下沿粗糙水平面由静止开始运动,发生位移s1后即撤去力F ,物体由运动一段距离后停止运动. 整个过程的V–t图线如图所示.求推力F与阻力f的比值.
F
s1
s
0 1 2 3 4
v
t
解法1.
由动能定理得 WF + Wf =0
即:Fs1 +( –fs)=0
由V–t图线知 s :s1 = 4 :1
所以 F :f = s :s1
结果:F :f = 4 :1
解法2. 分段用动能定理
F
s1
s
0 1 2 3 4
v
t
撤去F前,由动能定理得 (F – f)s1 =
mV2
V
mV2
撤去F后,由动能定理得 – f(s –s1) = 0 –
两式相加得 Fs1 +( –fs)= 0
由解法1 知 F :f = 4 :1
解法3. 牛顿定律结合匀变速直线运动规律
课堂小结
【典例1】(2021·江苏淮安市·高一月考)关于物体的动能,下列说法正确的是( )
A.物体的质量、速度不变,其动能一定不变
B.物体的动能不变,其速度一定不变
C.两个物体中,速度大的动能也大
D.某一过程中物体的速度变化,其动能一定变化
典例分析
【正确答案】A
【典例2】(2021·浙江高一月考)若物体在运动过程中受到的合外力不为零,经过一段时间,则( )
A.物体的动能可能不变
B.物体的动能一定变化
C.物体的加速度一定变化
D.物体速度方向一定变化
典例分析
【正确答案】A
【典例3】(2021·福建省福州格致中学高一月考)三个相同的小球a、b、c从相同高度开始运动,c水平抛出,b自由下落,a沿光滑斜面静止开始滚动。则( )
A.三个球落地的时间相同
B.三个球落地时的速度大小相同
C.落地时的重力的瞬时功率b球大于c球
D.c球落地时动能最大
典例分析
【正确答案】D
8.3
动能和动能定理
定义:物体因为运动而具有的能量称为动能。
奔驰中的汽车
投出的篮球
发射出的火箭
动能的大小与什么因素有关?
类型一:质量为m 的物体在与运动方向相同的恒力F 的作用下发生一段位移l ,速度从v1 增加到v2
类型二:质量为m 的物体在与运动方向相同的恒力F 的作用下,沿粗糙水平面运动了一段位移l ,受到的摩擦力为Ff ,速度从v1 变为v2
思考:
l
F
v2
Ff
F
v1
Ff
W合=Fl-Ff l = -
mv12
1
2
mv22
1
2
F
v1
F
v2
l
WF = Fl = -
mv12
1
2
mv22
1
2
1.定义:物体由于物体运动而具有的能量。
3.单位:焦耳(J) 1J=1kg·m2/s2
2.表达式:
4.标量:遵从代数运算法则,且只有正值。
5.状态量:对应某一时刻或某一位置,动能具有相对性。
动能的表达式
问题:对于质量一定的物体
(1)动能变化,速度是否一定变化?
(2)速度变化,动能是否一定变化?
6. 动能的变化:
v
v
v
否
是
ΔEk = Ek末Ek初
= Ek末Ek初
动能定理
1. 内容:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化。
W合=Ek2-Ek1
合力的功
末动能
初动能
2. 表达式:
W合=ΔEk
动能定理
(1)合力做正功,即W合>0,Ek2>Ek1 ,动能增大;
(2)合力做负功,即W合<0,Ek2<Ek1 ,动能减小。
4.动能定理的适用范围:
(1)恒力做功或变力做功;
(2)直线运动或曲线运动;
(3)单个物体或多个物体;
(4)一个过程或全过程。
3.对动能定理表达式 的说明:
W合=Ek2-Ek1
例1.一架喷气式飞机,质量 m 为 7.0×104kg,起飞过程中从静止开始滑跑。当位移l达到 2.5×103m 时,速度达到起飞速度 80 m/s。在此过程中,飞机受到的平均阻力是飞机所受重力的 1/50 。g取 10 m/s2,求飞机平均牵引力的大小。
F牵
x
v
F阻
l
O
分析 本题已知飞机滑跑过程的始、末速度,因而能够知道它在滑跑过程中增加的动能。根据动能定理,动能的增加等于牵引力做功和阻力做功的代数和。如图 ,在整个过程中,牵引力对飞机做正功、阻力做负功。由于飞机的位移和所受阻力已知,因而可以求得牵引力的大小
解 以飞机为研究对象, 设飞机滑跑的方向为x轴正方向。飞机的初动能Ek1=0,末动能 ,合力 F 做的功
根据动能定理 ,有
由于
把数值代入后得到
飞机平均牵引力的大小是 1.04×105N。
例2.物体沿高H的光滑斜面从顶端由静止下滑,求它滑到底端时的速度大小.
H
解:由动能定理得 mgH= mv2
∴v=
若物体沿高H的光滑曲面从顶端由静止下滑,结果如何?
仍由动能定理得 mgH= mv2
v=
若由H高处自由下落,结果如何呢?
仍为
v=
例3. 物体在恒定水平推力F的作用下沿粗糙水平面由静止开始运动,发生位移s1后即撤去力F ,物体由运动一段距离后停止运动. 整个过程的V–t图线如图所示.求推力F与阻力f的比值.
F
s1
s
0 1 2 3 4
v
t
解法1.
由动能定理得 WF + Wf =0
即:Fs1 +( –fs)=0
由V–t图线知 s :s1 = 4 :1
所以 F :f = s :s1
结果:F :f = 4 :1
解法2. 分段用动能定理
F
s1
s
0 1 2 3 4
v
t
撤去F前,由动能定理得 (F – f)s1 =
mV2
V
mV2
撤去F后,由动能定理得 – f(s –s1) = 0 –
两式相加得 Fs1 +( –fs)= 0
由解法1 知 F :f = 4 :1
解法3. 牛顿定律结合匀变速直线运动规律
课堂小结
【典例1】(2021·江苏淮安市·高一月考)关于物体的动能,下列说法正确的是( )
A.物体的质量、速度不变,其动能一定不变
B.物体的动能不变,其速度一定不变
C.两个物体中,速度大的动能也大
D.某一过程中物体的速度变化,其动能一定变化
典例分析
【正确答案】A
【典例2】(2021·浙江高一月考)若物体在运动过程中受到的合外力不为零,经过一段时间,则( )
A.物体的动能可能不变
B.物体的动能一定变化
C.物体的加速度一定变化
D.物体速度方向一定变化
典例分析
【正确答案】A
【典例3】(2021·福建省福州格致中学高一月考)三个相同的小球a、b、c从相同高度开始运动,c水平抛出,b自由下落,a沿光滑斜面静止开始滚动。则( )
A.三个球落地的时间相同
B.三个球落地时的速度大小相同
C.落地时的重力的瞬时功率b球大于c球
D.c球落地时动能最大
典例分析
【正确答案】D
