人教版(B版2019课标)高中数学必修四11.1.5旋转体 学案
文档属性
| 名称 | 人教版(B版2019课标)高中数学必修四11.1.5旋转体 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 11:11:57 | ||
图片预览


文档简介
旋转体
【学习目标】
1.通过圆柱、圆锥、圆台、球的定义及结构特征的学习,培养直观想象的数学核心素养。
2.借助旋转体的轴截面的学习,提升数学运算的数学核心素养。
【学习重难点】
1.了解圆柱、圆锥、圆台、球的定义。(重点)
2.掌握圆柱、圆锥、圆台、球的结构特征。(重点)
3.能够根据圆柱、圆锥、圆台、球的结构特征识别和区分几何体。(难点)
4.会作旋转体的轴截面,并利用轴截面解决问题。(难点)
【学习过程】
一、初试身手
1.圆锥的母线长为10,底面半径为6,则其高等于( )
A.6 B.8
C.10 D.不确定
2.有下列说法:
①球的半径是球面上任意一点与球心的连线;
②球的直径是球面上任意两点间的连线;
③用一个平面截一个球,得到的是一个圆。
其中正确说法的序号是________。
二、新知探究
1.旋转体的结构特征
【例1】 判断下列各命题是否正确
(1)圆柱上底面圆上任一点与下底面圆上任一点的连线都是圆柱的母线;
(2)一直角梯形绕下底所在直线旋转一周,所形成的曲面围成的几何体是圆台;
(3)圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形;
(4)到定点的距离等于定长的点的集合是球。
2.旋转体中的计算
[探究问题]
1.圆柱、圆锥、圆台平行于底面的截面是什么样的图形?
[提示] 圆面。
2.圆柱、圆锥、圆台过轴的截面是什么样的图形?
[提示] 分别为矩形、等腰三角形、等腰梯形。
3.经过圆台的任意两条母线作截面,截面是什么图形?
[提示] 因为圆台可以看成是圆锥被平行于底面的平面所截得到的几何体,所以任意两条母线长度均相等,且延长后相交,故经过这两条母线的截面是以这两条母线为腰的等腰梯形。
4.球的截面是什么?
[提示] 球的截面均是圆面,球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做球的小圆。
【例2】 一个圆台的母线长为12 cm,两底面面积分别为4π cm2和25π cm2,求圆台的高。
[思路探究] 作出圆台的轴截面,是一个等腰梯形。
【母题探究】
1.将圆台还原为圆锥后,求圆锥的母线长。
2.如图,在底面半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的底面半径。
【学习小结】
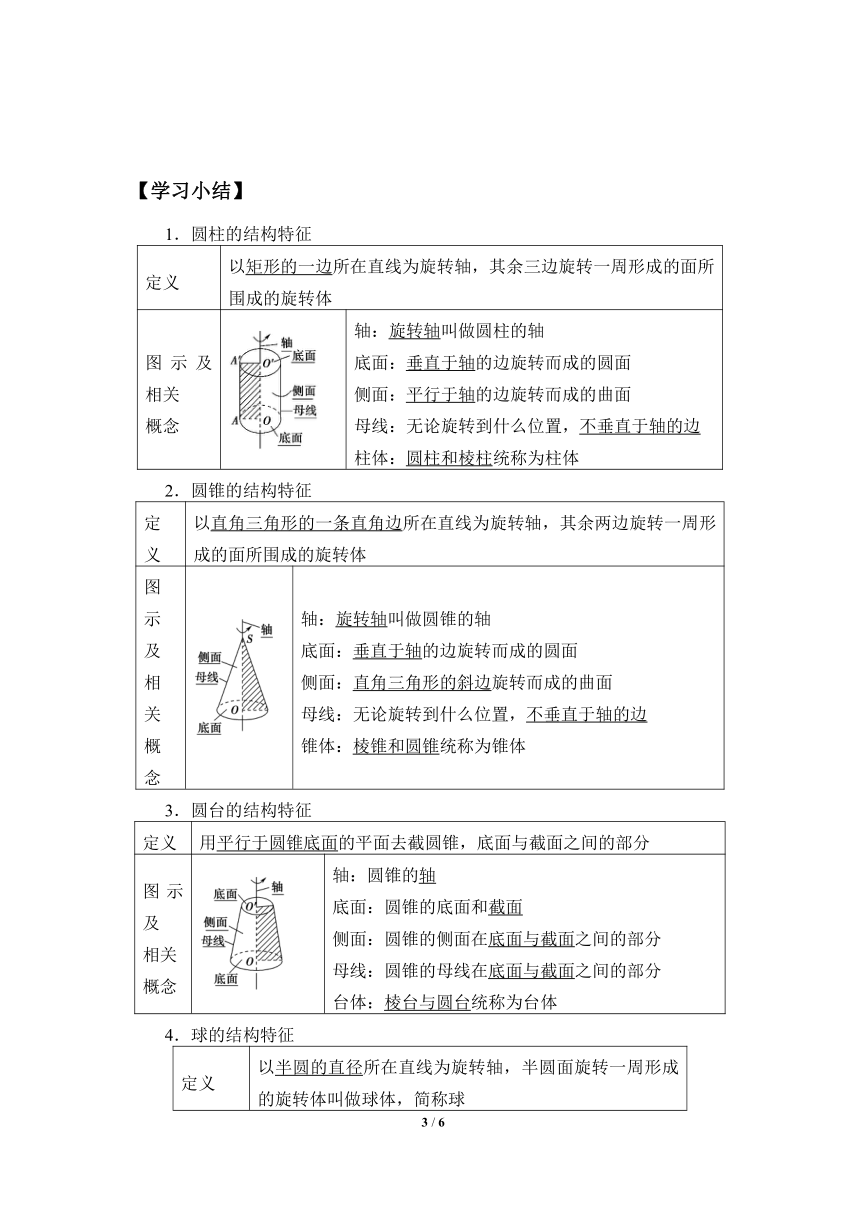
1.圆柱的结构特征
定义 以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体
图示及相关 概念 轴:旋转轴叫做圆柱的轴 底面:垂直于轴的边旋转而成的圆面 侧面:平行于轴的边旋转而成的曲面 母线:无论旋转到什么位置,不垂直于轴的边 柱体:圆柱和棱柱统称为柱体
2.圆锥的结构特征
定义 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体
图示及相关概念 轴:旋转轴叫做圆锥的轴 底面:垂直于轴的边旋转而成的圆面 侧面:直角三角形的斜边旋转而成的曲面 母线:无论旋转到什么位置,不垂直于轴的边 锥体:棱锥和圆锥统称为锥体
3.圆台的结构特征
定义 用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分
图示及 相关 概念 轴:圆锥的轴 底面:圆锥的底面和截面 侧面:圆锥的侧面在底面与截面之间的部分 母线:圆锥的母线在底面与截面之间的部分 台体:棱台与圆台统称为台体
4.球的结构特征
定义 以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球
图示及相关 概念 球心:半圆的圆心 半径:半圆的半径 直径:半圆的直径
【精炼反馈】
1.判断(正确的打“√”,错误的打“×”)
(1)矩形绕其一边所在直线旋转一周而形成的曲面所围成的几何体是圆柱。 ( )
(2)以直角梯形的一腰为轴旋转所得的旋转体是圆台。 ( )
(3)用一个平面去截圆锥,得到一个圆锥和一个圆台。 ( )
2.正方形绕其一条对角线所在直线旋转一周,所得几何体是( )
A.圆柱 B.圆锥
C.圆台 D.两个圆锥
3.如图所示的几何体是由简单几何体________构成的。
答案:
【学习过程】
一、初试身手
1.B [由圆锥的轴截面可知,圆锥的母线、底面半径与高构成直角三角形,所以其高为=8.]
2.① [利用球的结构特征判断:①正确;②不正确,因为直径必过球心;③不正确,因为得到的是一个圆面。]
【例1】
[解](1)错。由圆柱母线的定义知,圆柱的母线应平行于轴。
(2)错。直角梯形绕下底所在直线旋转一周所形成的几何体是由一个圆柱与一个圆锥组成的简单组合体,如图所示。
(3)正确。
(4)错。应为球面。
【例2】
[解] 圆台的轴截面是等腰梯形ABCD(如图所示)。
由已知可得O1A=2 cm,OB=5 cm。
又由题意知,腰长为12 cm,
所以高AM=
=3(cm)。
【母题探究】
1.[解] 如图所示,延长BA,OO1,CD,交于点S,
设截得此圆台的圆锥的母线长为l,
则由△SAO1∽△SBO,可得=,解得l=20 cm。
即截得此圆台的圆锥的母线长为20 cm。
2.[解] 设圆锥的底面半径为R,圆柱的底面半径为r,则由三角形相似,
得=,
即1-=,解得r=1.
即圆柱的底面半径为1.
【精炼反馈】
1.[答案] (1)√ (2)× (3)×
[提示] (1)正确;(2)错误,应以直角梯形的垂直于底边的腰为轴;(3)错误,应是平面与圆锥底面平行。
2.D [连接正方形的两条对角线知对角线互相垂直,故绕对角线旋转一周形成两个圆锥。]
3.[答案] 四棱台和球
4.[解] 设圆柱底面半径为r,母线为l,则由题意得
解得r=。
所以此圆柱的底面半径为
5 / 6
【学习目标】
1.通过圆柱、圆锥、圆台、球的定义及结构特征的学习,培养直观想象的数学核心素养。
2.借助旋转体的轴截面的学习,提升数学运算的数学核心素养。
【学习重难点】
1.了解圆柱、圆锥、圆台、球的定义。(重点)
2.掌握圆柱、圆锥、圆台、球的结构特征。(重点)
3.能够根据圆柱、圆锥、圆台、球的结构特征识别和区分几何体。(难点)
4.会作旋转体的轴截面,并利用轴截面解决问题。(难点)
【学习过程】
一、初试身手
1.圆锥的母线长为10,底面半径为6,则其高等于( )
A.6 B.8
C.10 D.不确定
2.有下列说法:
①球的半径是球面上任意一点与球心的连线;
②球的直径是球面上任意两点间的连线;
③用一个平面截一个球,得到的是一个圆。
其中正确说法的序号是________。
二、新知探究
1.旋转体的结构特征
【例1】 判断下列各命题是否正确
(1)圆柱上底面圆上任一点与下底面圆上任一点的连线都是圆柱的母线;
(2)一直角梯形绕下底所在直线旋转一周,所形成的曲面围成的几何体是圆台;
(3)圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形;
(4)到定点的距离等于定长的点的集合是球。
2.旋转体中的计算
[探究问题]
1.圆柱、圆锥、圆台平行于底面的截面是什么样的图形?
[提示] 圆面。
2.圆柱、圆锥、圆台过轴的截面是什么样的图形?
[提示] 分别为矩形、等腰三角形、等腰梯形。
3.经过圆台的任意两条母线作截面,截面是什么图形?
[提示] 因为圆台可以看成是圆锥被平行于底面的平面所截得到的几何体,所以任意两条母线长度均相等,且延长后相交,故经过这两条母线的截面是以这两条母线为腰的等腰梯形。
4.球的截面是什么?
[提示] 球的截面均是圆面,球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做球的小圆。
【例2】 一个圆台的母线长为12 cm,两底面面积分别为4π cm2和25π cm2,求圆台的高。
[思路探究] 作出圆台的轴截面,是一个等腰梯形。
【母题探究】
1.将圆台还原为圆锥后,求圆锥的母线长。
2.如图,在底面半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的底面半径。
【学习小结】
1.圆柱的结构特征
定义 以矩形的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体
图示及相关 概念 轴:旋转轴叫做圆柱的轴 底面:垂直于轴的边旋转而成的圆面 侧面:平行于轴的边旋转而成的曲面 母线:无论旋转到什么位置,不垂直于轴的边 柱体:圆柱和棱柱统称为柱体
2.圆锥的结构特征
定义 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体
图示及相关概念 轴:旋转轴叫做圆锥的轴 底面:垂直于轴的边旋转而成的圆面 侧面:直角三角形的斜边旋转而成的曲面 母线:无论旋转到什么位置,不垂直于轴的边 锥体:棱锥和圆锥统称为锥体
3.圆台的结构特征
定义 用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分
图示及 相关 概念 轴:圆锥的轴 底面:圆锥的底面和截面 侧面:圆锥的侧面在底面与截面之间的部分 母线:圆锥的母线在底面与截面之间的部分 台体:棱台与圆台统称为台体
4.球的结构特征
定义 以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球
图示及相关 概念 球心:半圆的圆心 半径:半圆的半径 直径:半圆的直径
【精炼反馈】
1.判断(正确的打“√”,错误的打“×”)
(1)矩形绕其一边所在直线旋转一周而形成的曲面所围成的几何体是圆柱。 ( )
(2)以直角梯形的一腰为轴旋转所得的旋转体是圆台。 ( )
(3)用一个平面去截圆锥,得到一个圆锥和一个圆台。 ( )
2.正方形绕其一条对角线所在直线旋转一周,所得几何体是( )
A.圆柱 B.圆锥
C.圆台 D.两个圆锥
3.如图所示的几何体是由简单几何体________构成的。
答案:
【学习过程】
一、初试身手
1.B [由圆锥的轴截面可知,圆锥的母线、底面半径与高构成直角三角形,所以其高为=8.]
2.① [利用球的结构特征判断:①正确;②不正确,因为直径必过球心;③不正确,因为得到的是一个圆面。]
【例1】
[解](1)错。由圆柱母线的定义知,圆柱的母线应平行于轴。
(2)错。直角梯形绕下底所在直线旋转一周所形成的几何体是由一个圆柱与一个圆锥组成的简单组合体,如图所示。
(3)正确。
(4)错。应为球面。
【例2】
[解] 圆台的轴截面是等腰梯形ABCD(如图所示)。
由已知可得O1A=2 cm,OB=5 cm。
又由题意知,腰长为12 cm,
所以高AM=
=3(cm)。
【母题探究】
1.[解] 如图所示,延长BA,OO1,CD,交于点S,
设截得此圆台的圆锥的母线长为l,
则由△SAO1∽△SBO,可得=,解得l=20 cm。
即截得此圆台的圆锥的母线长为20 cm。
2.[解] 设圆锥的底面半径为R,圆柱的底面半径为r,则由三角形相似,
得=,
即1-=,解得r=1.
即圆柱的底面半径为1.
【精炼反馈】
1.[答案] (1)√ (2)× (3)×
[提示] (1)正确;(2)错误,应以直角梯形的垂直于底边的腰为轴;(3)错误,应是平面与圆锥底面平行。
2.D [连接正方形的两条对角线知对角线互相垂直,故绕对角线旋转一周形成两个圆锥。]
3.[答案] 四棱台和球
4.[解] 设圆柱底面半径为r,母线为l,则由题意得
解得r=。
所以此圆柱的底面半径为
5 / 6
