2021—2022学年鲁教版(五四制)数学九年级上册 1.3反比例函数的应用 课件(共20张PPT)
文档属性
| 名称 | 2021—2022学年鲁教版(五四制)数学九年级上册 1.3反比例函数的应用 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 923.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 08:18:39 | ||
图片预览







文档简介
(共20张PPT)
鲁教版(五四制)数学九年级上册
第一章 反比例函数
1.3 反比例函数的应用
教学目标
1.利用反比例函数的知识分析、解决实际间题。
2.渗透数形结合思想,提高学生用函数观点解诀问题的能力。
如图,直线 与反比例函数 的图象交于A ,
B 两点.
(1)求k1、k2的值;
(2)直接写出
时,x的取值范围;
_
_
_
_
_
O
A
B
x
y
(1,6)
(a,3)
复习回顾
某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?
当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化?
新知探究
如果人和木板对湿地地面
的压力合计600N,那么
(1)用含S的代数式表示P,
P是S的反比例函数吗?
为什么?
P是S的反比例函数.
解:
新知探究
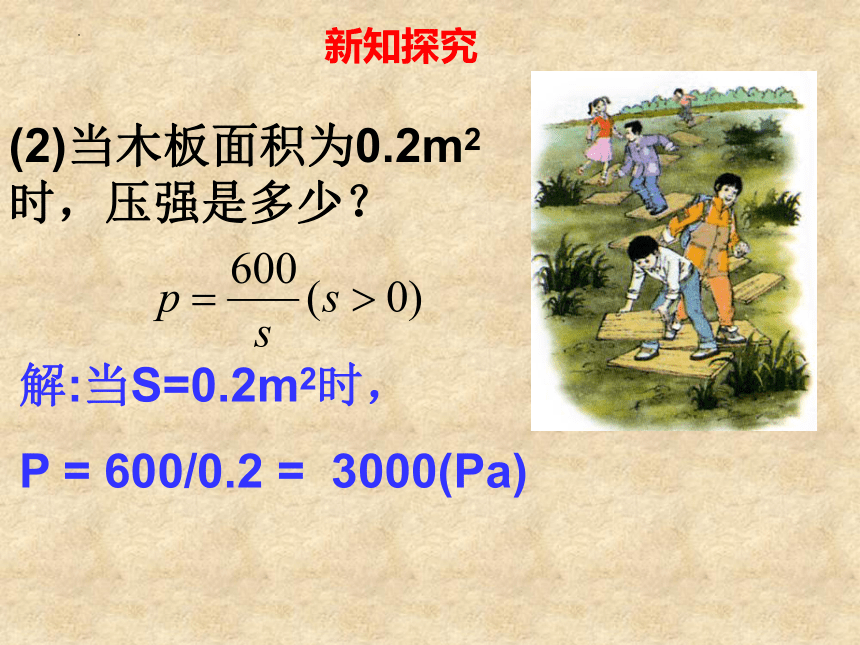
(2)当木板面积为0.2m2时,压强是多少?
解:当S=0.2m2时,
P = 600/0.2 = 3000(Pa)
新知探究
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
解:当P≤6000时,S≥600/6000=0.1(m2)
所以木板面积至少要0.1m2.
新知探究
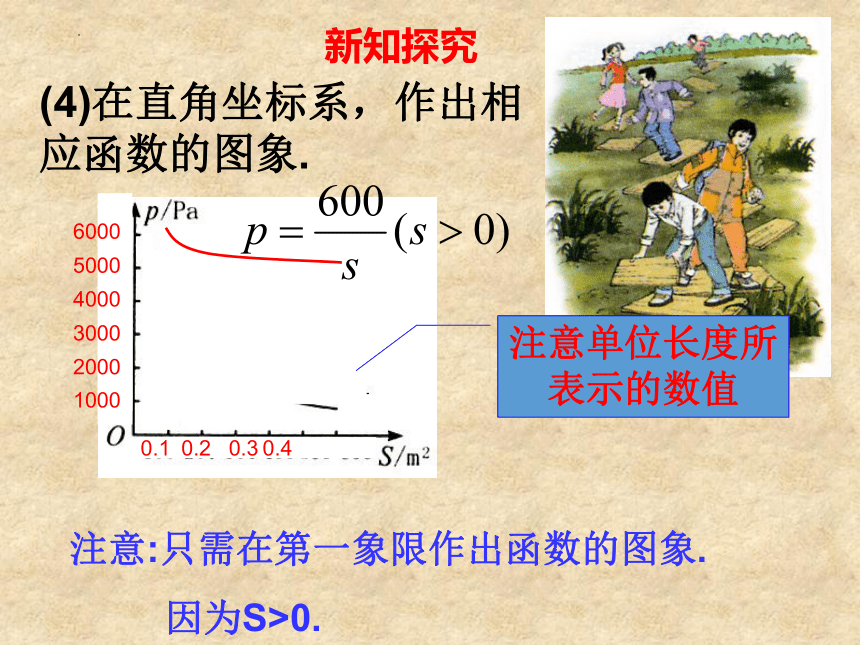
(4)在直角坐标系,作出相应函数的图象.
注意:只需在第一象限作出函数的图象.
因为S>0.
注意单位长度所表示的数值
0.1
0.2
0.3
0.4
1000
2000
3000
4000
5000
6000
新知探究
根据图象,回答:(2)当木板面积为0.2m2时,压强是多少?
0.1
0.2
0.3
0.4
1000
2000
3000
4000
5000
6000
新知探究
如图,正比例函数y= k x的图象与反比例函数y=k /x的图象相交于A、B两点,其中点A的坐标为
(1)写出这两个函数表达式;
解:(1)把A点坐标 分别代入 y=k1x, 和 y=k2/x, 解得:k1=2.k2=6
所以所求的函数表达式为:y=2x,和y=6/x.
x
y
A
B
O
1
2
课堂练习
(2)你能求出点B的坐标吗?
你是怎样求的?
解:B点的坐标是两个函数组成的方程组的另一个解.
x
y
A
B
O
x=
某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(1)蓄水池的容积是多少?
解:蓄水池的容积为:8×6=48(m3).
(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?
答:此时所需时间t(h)将减少.
(3)写出t与Q之间的函数关系式;
解:t与Q之间的函数关系式为:
(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?
解:当t=5h时,Q=48/5=9.6m3.
所以每时的排水量至少为9.6m3.
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空?
解:当Q=12(m3)时,t=48/12=4(h).
所以最少需5h可将满池水全部排空.
某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)写出这一函数表达式; (2)当气体体积1m3为时,气压时多少? (3)当气球内的气压大于140kpa时,
气球将爆炸,为了安全起见,
气体的体积应不小于多少?
V/m3
P/kpa
.
A(0.8,120)
x
y
A
B
O
(1,3)
0下列函数中哪些是正比例函数?哪些是反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
y = 3x
y =
3
2x
y =
1
3x
y =
x
1
复习提问
1.小明家买了1000度电,设平均每天用电x度,这些点能够使用y天.
(1)写出y与x之间的函数关系式.
(2)当平均每天用电5度时,这些电可以用多少天?
(3)如果这些电用了250天,那么平均每天用电多少度?
解:
答:当平均每天用电5度时,这些电可以用200天.
如果这些电用了250天,那么平均每天用电4度.
巩固提高
2.一块重约为30N的物块,放在地面上.
(1)写出用这物块的受力面积S(m )表示它对地面的压强p(Pa)的函数表达式.
(2)画出这个函数的图像.
(3)如果这个物体的长方体形的,长、宽、高分别为24cm,12cm和6cm,求放置方式不同时,这个物体对地面的压强分别是多大.
解:
(2)经过列表,描点,连线即可的到该函数的图像.
(3)底面为24cm,12cm时:
底面为24cm,6cm时:
底面为12cm ,6cm时:
函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
从函数的图象中获取信息的能力是学好数学必需具有的基本素质.
课堂总结
谢谢观赏
鲁教版(五四制)数学九年级上册
第一章 反比例函数
1.3 反比例函数的应用
教学目标
1.利用反比例函数的知识分析、解决实际间题。
2.渗透数形结合思想,提高学生用函数观点解诀问题的能力。
如图,直线 与反比例函数 的图象交于A ,
B 两点.
(1)求k1、k2的值;
(2)直接写出
时,x的取值范围;
_
_
_
_
_
O
A
B
x
y
(1,6)
(a,3)
复习回顾
某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?
当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化?
新知探究
如果人和木板对湿地地面
的压力合计600N,那么
(1)用含S的代数式表示P,
P是S的反比例函数吗?
为什么?
P是S的反比例函数.
解:
新知探究
(2)当木板面积为0.2m2时,压强是多少?
解:当S=0.2m2时,
P = 600/0.2 = 3000(Pa)
新知探究
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
解:当P≤6000时,S≥600/6000=0.1(m2)
所以木板面积至少要0.1m2.
新知探究
(4)在直角坐标系,作出相应函数的图象.
注意:只需在第一象限作出函数的图象.
因为S>0.
注意单位长度所表示的数值
0.1
0.2
0.3
0.4
1000
2000
3000
4000
5000
6000
新知探究
根据图象,回答:(2)当木板面积为0.2m2时,压强是多少?
0.1
0.2
0.3
0.4
1000
2000
3000
4000
5000
6000
新知探究
如图,正比例函数y= k x的图象与反比例函数y=k /x的图象相交于A、B两点,其中点A的坐标为
(1)写出这两个函数表达式;
解:(1)把A点坐标 分别代入 y=k1x, 和 y=k2/x, 解得:k1=2.k2=6
所以所求的函数表达式为:y=2x,和y=6/x.
x
y
A
B
O
1
2
课堂练习
(2)你能求出点B的坐标吗?
你是怎样求的?
解:B点的坐标是两个函数组成的方程组的另一个解.
x
y
A
B
O
x=
某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(1)蓄水池的容积是多少?
解:蓄水池的容积为:8×6=48(m3).
(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?
答:此时所需时间t(h)将减少.
(3)写出t与Q之间的函数关系式;
解:t与Q之间的函数关系式为:
(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?
解:当t=5h时,Q=48/5=9.6m3.
所以每时的排水量至少为9.6m3.
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空?
解:当Q=12(m3)时,t=48/12=4(h).
所以最少需5h可将满池水全部排空.
某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)写出这一函数表达式; (2)当气体体积1m3为时,气压时多少? (3)当气球内的气压大于140kpa时,
气球将爆炸,为了安全起见,
气体的体积应不小于多少?
V/m3
P/kpa
.
A(0.8,120)
x
y
A
B
O
(1,3)
0
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
y = 3x
y =
3
2x
y =
1
3x
y =
x
1
复习提问
1.小明家买了1000度电,设平均每天用电x度,这些点能够使用y天.
(1)写出y与x之间的函数关系式.
(2)当平均每天用电5度时,这些电可以用多少天?
(3)如果这些电用了250天,那么平均每天用电多少度?
解:
答:当平均每天用电5度时,这些电可以用200天.
如果这些电用了250天,那么平均每天用电4度.
巩固提高
2.一块重约为30N的物块,放在地面上.
(1)写出用这物块的受力面积S(m )表示它对地面的压强p(Pa)的函数表达式.
(2)画出这个函数的图像.
(3)如果这个物体的长方体形的,长、宽、高分别为24cm,12cm和6cm,求放置方式不同时,这个物体对地面的压强分别是多大.
解:
(2)经过列表,描点,连线即可的到该函数的图像.
(3)底面为24cm,12cm时:
底面为24cm,6cm时:
底面为12cm ,6cm时:
函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
从函数的图象中获取信息的能力是学好数学必需具有的基本素质.
课堂总结
谢谢观赏
