高中数学必修四11.3.1平行直线与异面直线 学案(含答案)
文档属性
| 名称 | 高中数学必修四11.3.1平行直线与异面直线 学案(含答案) | 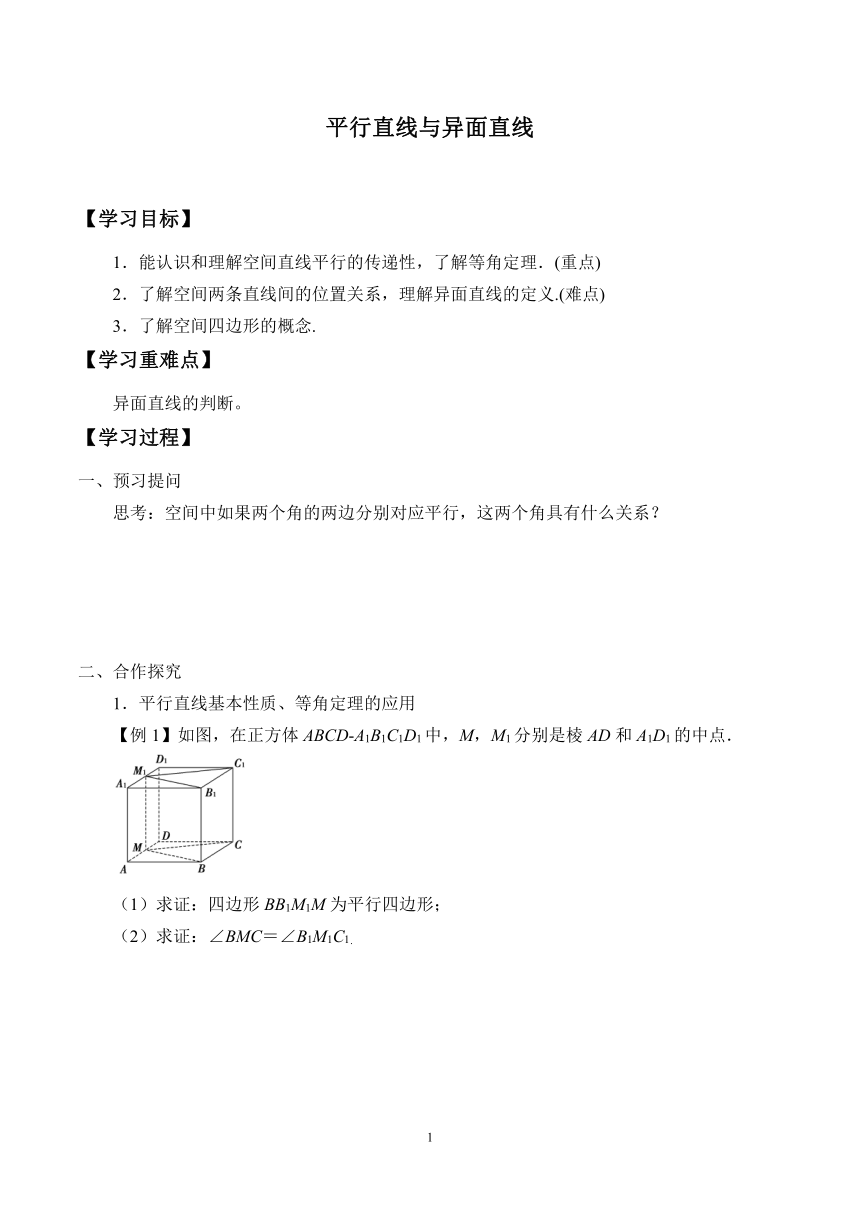 | |
| 格式 | zip | ||
| 文件大小 | 119.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 17:26:24 | ||
图片预览



文档简介
平行直线与异面直线
【学习目标】
1.能认识和理解空间直线平行的传递性,了解等角定理.(重点)
2.了解空间两条直线间的位置关系,理解异面直线的定义.(难点)
3.了解空间四边形的概念.
【学习重难点】
异面直线的判断。
【学习过程】
一、预习提问
思考:空间中如果两个角的两边分别对应平行,这两个角具有什么关系?
二、合作探究
1.平行直线基本性质、等角定理的应用
【例1】如图,在正方体ABCD A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
[思路探究](1)欲证四边形BB1M1M是平行四边形,可证其一组对边平行且相等;(2)可结合(1)利用等角定理证明或利用三角形全等证明.
[证明] (1)∵ABCD A1B1C1D1为正方体.
∴AD=A1D1,且AD∥A1D1,
又M、M1分别为棱AD.A1D1的中点,
∴AM=A1M1且AM∥A1M1,
∴四边形AMM1A1为平行四边形,
∴MM1=AA1且MM1∥AA1.
又AA1=BB1且AA1∥BB1,
∴MM1=BB1且MM1∥BB1,
∴四边形BB1M1M为平行四边形.
(2)法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
∵∠BMC和∠B1M1C1方向相同,
∴∠BMC=∠B1M1C1.
法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1=CM.
又∵B1C1=BC,∴△BCM≌△B1C1M1,
∴∠BMC=∠B1M1C1.
【规律方法】
(1)空间两条直线平行的证明
一是定义法:即证明两条直线在同一个平面内且两直线没有公共点;
二是利用平面图形的有关平行的性质,如三角形中位线,梯形,平行四边形等关于平行的性质;
三是利用平行直线基本性质:找到一条直线,使所证的直线都与这条直线平行.
(2)求证角相等
一是用等角定理;二是用三角形全等或相似.
2.异面直线与空间四边形
【例2】如图,在长方体ABCD A1B1C1D1中,判断下列直线的位置关系:
①直线A1B与直线D1C的位置关系是________;
②直线A1B与直线B1C的位置关系是________;
③直线D1D与直线D1C的位置关系是________;
④直线AB与直线B1C的位置关系是________.
【解析】经探究可知直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线平行,所以①应该填“平行”;点A1.B.B1在平面A1BB1内,而C不在平面A1BB1内,则直线A1B与直线B1C异面.同理,直线AB与直线B1C异面.所以②④应该填“异面”;直线D1D与直线D1C相交于D1点,所以③应该填“相交”.
【答案】①平行 ②异面 ③相交 ④异面
【规律方法】判定两条直线是异面直线的方法:
①定义法:由定义判断两直线不可能在同一平面内;
②重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图).
【例3】如图所示,A,B,C,D为不共面的四点,E,F,G,H分别在线段AB,BC,CD,DA上.
(1)如果EH∩FG=P,那么点P在直线________上.
(2)如果EF∩GH=Q,那么点Q在直线________上.
【解析】(1)BD (2)AC [(1)若EH∩FG=P,
那么点P∈平面ABD,P∈平面BCD,
而平面ABD∩平面BCD=BD,
所以P∈BD.
(2)若EF∩GH=Q,则点Q∈平面ABC,Q∈平面ACD,而平面ABC∩平面ACD=AC,所以Q∈AC.]
【学习小结】
1.平行直线基本性质
文字表述:平行于同一条直线的两条直线互相平行.这一性质叫做空间平行线的传递性.
符号表述: a∥c.
2.等角定理
如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.
3.异面直线
①定义:把不同在任何一个平面内的两条直线叫做异面直线;
②画法:(通常用平面衬托)
4.空间四边形
①定义:顺次连接不共面的4点所构成的图形称为空间四边形,其中4个点都是空间四边形的顶点,连接相邻顶点间的线段称为空间四边形的边,连接不相邻顶点间的线段称为空间四边形的对角线.;
②画法:
【精炼反馈】
1.思考辨析
(1)若直线与平面不相交,则直线与平面平行.( )
(2)过一点有且只有一条直线与已知直线平行.( )
(3)直线l上有无数多个点在平面α外,则l∥α.( )
(4)过平面外一点有且只有一条直线与该平面平行.( )
[解析] (1)错误.若直线与平面不相交,则直线在平面内或直线与平面平行.
(2)错误.当点在已知直线上时,不存在过该点的直线与已知直线平行,故(2)错.
(3)错误.直线l也可能与平面α相交.
(4)错误.在棱柱的上底面内,过一点任意作一条直线都与棱柱的下底面平行,所以过平面外一点与已知平面平行的直线有无数条,故(4)错.
[答案] (1)× (2)× (3)× (4)×
2.如图所示,在三棱锥S MNP中,E、F、G、H分别是棱SN、SP、MN、MP的中点,则EF与HG的位置关系是( )
A.平行
B.相交
C.异面
D.平行或异面
A [∵E、F分别是SN和SP的中点,
∴EF∥PN.同理可证HG∥PN,
∴EF∥HG.]
3.已知角α和角β的两边分别平行且一组边方向相同,另一组边的方向相反,若α=45°,则β=________.
135° [由等角定理可知β=135°.]
4.证明:若两个相交平面分别过两条平行直线,则它们的交线和这两条平行直线平行.
[解] 已知:a∥b,a α,b β,α∩β=l.求证:a∥b∥l.
证明:如图所示,
∵a∥b,b β,
∴a∥β,
又a α,α∩β=l,
∴a∥l,
又a∥b,
∴a∥b∥l.
4
【学习目标】
1.能认识和理解空间直线平行的传递性,了解等角定理.(重点)
2.了解空间两条直线间的位置关系,理解异面直线的定义.(难点)
3.了解空间四边形的概念.
【学习重难点】
异面直线的判断。
【学习过程】
一、预习提问
思考:空间中如果两个角的两边分别对应平行,这两个角具有什么关系?
二、合作探究
1.平行直线基本性质、等角定理的应用
【例1】如图,在正方体ABCD A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
[思路探究](1)欲证四边形BB1M1M是平行四边形,可证其一组对边平行且相等;(2)可结合(1)利用等角定理证明或利用三角形全等证明.
[证明] (1)∵ABCD A1B1C1D1为正方体.
∴AD=A1D1,且AD∥A1D1,
又M、M1分别为棱AD.A1D1的中点,
∴AM=A1M1且AM∥A1M1,
∴四边形AMM1A1为平行四边形,
∴MM1=AA1且MM1∥AA1.
又AA1=BB1且AA1∥BB1,
∴MM1=BB1且MM1∥BB1,
∴四边形BB1M1M为平行四边形.
(2)法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
∵∠BMC和∠B1M1C1方向相同,
∴∠BMC=∠B1M1C1.
法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1=CM.
又∵B1C1=BC,∴△BCM≌△B1C1M1,
∴∠BMC=∠B1M1C1.
【规律方法】
(1)空间两条直线平行的证明
一是定义法:即证明两条直线在同一个平面内且两直线没有公共点;
二是利用平面图形的有关平行的性质,如三角形中位线,梯形,平行四边形等关于平行的性质;
三是利用平行直线基本性质:找到一条直线,使所证的直线都与这条直线平行.
(2)求证角相等
一是用等角定理;二是用三角形全等或相似.
2.异面直线与空间四边形
【例2】如图,在长方体ABCD A1B1C1D1中,判断下列直线的位置关系:
①直线A1B与直线D1C的位置关系是________;
②直线A1B与直线B1C的位置关系是________;
③直线D1D与直线D1C的位置关系是________;
④直线AB与直线B1C的位置关系是________.
【解析】经探究可知直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线平行,所以①应该填“平行”;点A1.B.B1在平面A1BB1内,而C不在平面A1BB1内,则直线A1B与直线B1C异面.同理,直线AB与直线B1C异面.所以②④应该填“异面”;直线D1D与直线D1C相交于D1点,所以③应该填“相交”.
【答案】①平行 ②异面 ③相交 ④异面
【规律方法】判定两条直线是异面直线的方法:
①定义法:由定义判断两直线不可能在同一平面内;
②重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图).
【例3】如图所示,A,B,C,D为不共面的四点,E,F,G,H分别在线段AB,BC,CD,DA上.
(1)如果EH∩FG=P,那么点P在直线________上.
(2)如果EF∩GH=Q,那么点Q在直线________上.
【解析】(1)BD (2)AC [(1)若EH∩FG=P,
那么点P∈平面ABD,P∈平面BCD,
而平面ABD∩平面BCD=BD,
所以P∈BD.
(2)若EF∩GH=Q,则点Q∈平面ABC,Q∈平面ACD,而平面ABC∩平面ACD=AC,所以Q∈AC.]
【学习小结】
1.平行直线基本性质
文字表述:平行于同一条直线的两条直线互相平行.这一性质叫做空间平行线的传递性.
符号表述: a∥c.
2.等角定理
如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.
3.异面直线
①定义:把不同在任何一个平面内的两条直线叫做异面直线;
②画法:(通常用平面衬托)
4.空间四边形
①定义:顺次连接不共面的4点所构成的图形称为空间四边形,其中4个点都是空间四边形的顶点,连接相邻顶点间的线段称为空间四边形的边,连接不相邻顶点间的线段称为空间四边形的对角线.;
②画法:
【精炼反馈】
1.思考辨析
(1)若直线与平面不相交,则直线与平面平行.( )
(2)过一点有且只有一条直线与已知直线平行.( )
(3)直线l上有无数多个点在平面α外,则l∥α.( )
(4)过平面外一点有且只有一条直线与该平面平行.( )
[解析] (1)错误.若直线与平面不相交,则直线在平面内或直线与平面平行.
(2)错误.当点在已知直线上时,不存在过该点的直线与已知直线平行,故(2)错.
(3)错误.直线l也可能与平面α相交.
(4)错误.在棱柱的上底面内,过一点任意作一条直线都与棱柱的下底面平行,所以过平面外一点与已知平面平行的直线有无数条,故(4)错.
[答案] (1)× (2)× (3)× (4)×
2.如图所示,在三棱锥S MNP中,E、F、G、H分别是棱SN、SP、MN、MP的中点,则EF与HG的位置关系是( )
A.平行
B.相交
C.异面
D.平行或异面
A [∵E、F分别是SN和SP的中点,
∴EF∥PN.同理可证HG∥PN,
∴EF∥HG.]
3.已知角α和角β的两边分别平行且一组边方向相同,另一组边的方向相反,若α=45°,则β=________.
135° [由等角定理可知β=135°.]
4.证明:若两个相交平面分别过两条平行直线,则它们的交线和这两条平行直线平行.
[解] 已知:a∥b,a α,b β,α∩β=l.求证:a∥b∥l.
证明:如图所示,
∵a∥b,b β,
∴a∥β,
又a α,α∩β=l,
∴a∥l,
又a∥b,
∴a∥b∥l.
4
