五年级数学下册课件 7解决问题的策略 苏教版(共32张PPT)
文档属性
| 名称 | 五年级数学下册课件 7解决问题的策略 苏教版(共32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 16:33:10 | ||
图片预览



文档简介
(共32张PPT)
解决问题的策略
苏教版《义务教育教科书 数学》
五年级下册
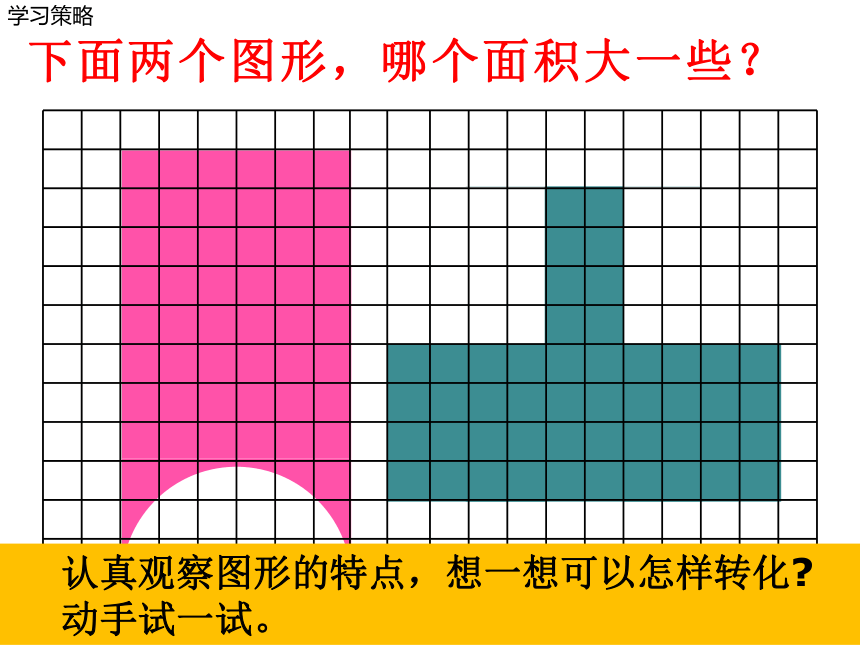
下面两个图形,哪个面积大一些?
认真观察图形的特点,想一想可以怎样转化
动手试一试。
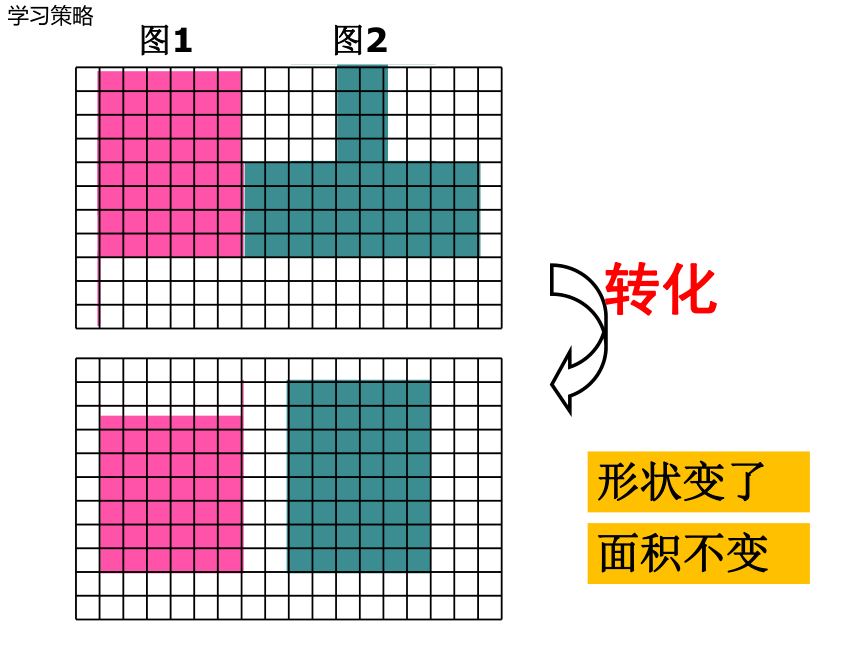
学习策略
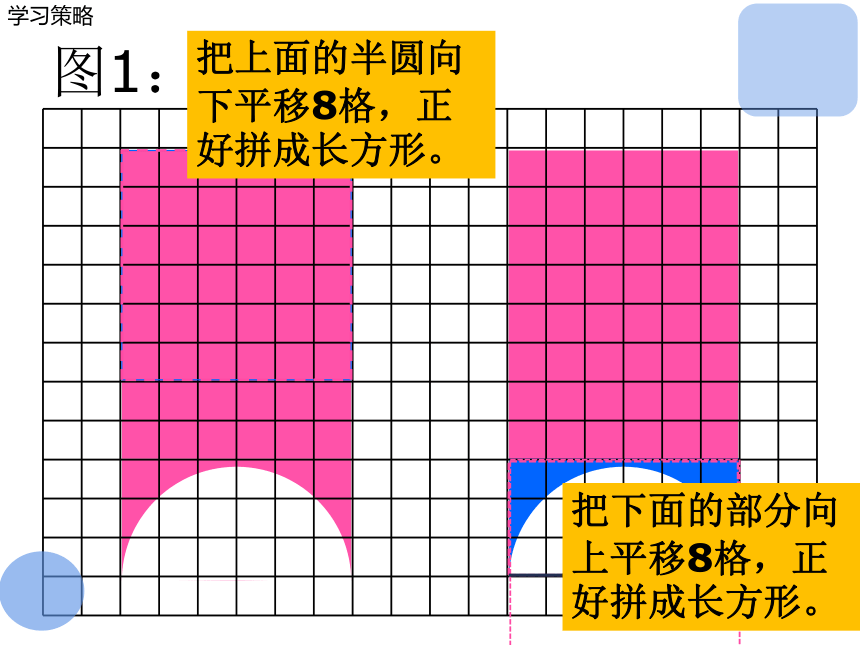
图1:
学习策略
把上面的半圆向下平移8格,正好拼成长方形。
把下面的部分向上平移8格,正好拼成长方形。
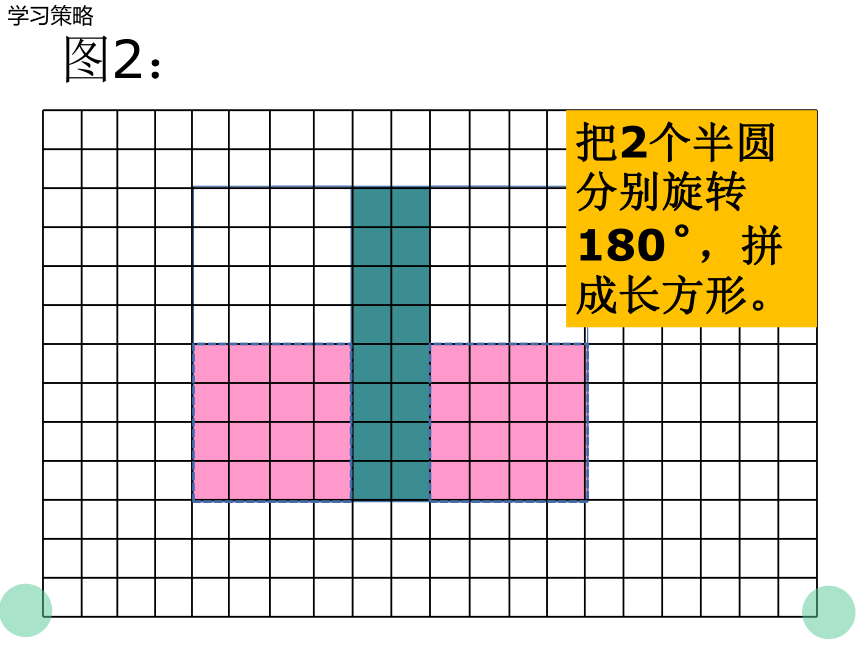
图2:
把2个半圆
分别旋转180 ,拼成长方形。
学习策略
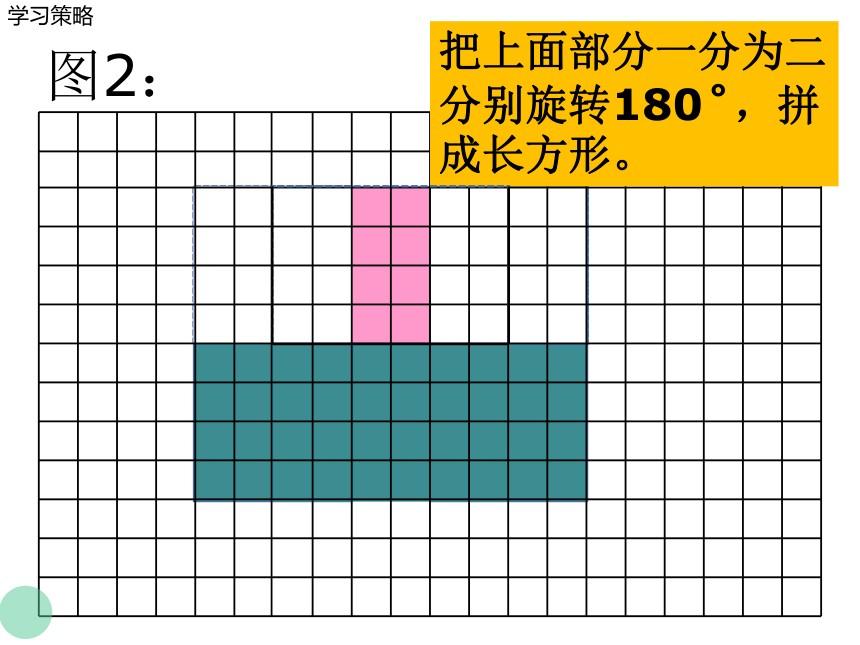
图2:
把上面部分一分为二分别旋转180 ,拼成长方形。
学习策略
学习策略
6
8
4
12
转化
形状变了
面积不变
学习策略
图1
图2
我们曾经用转化的策略解决过哪些问题?
小乘
小除
异分母
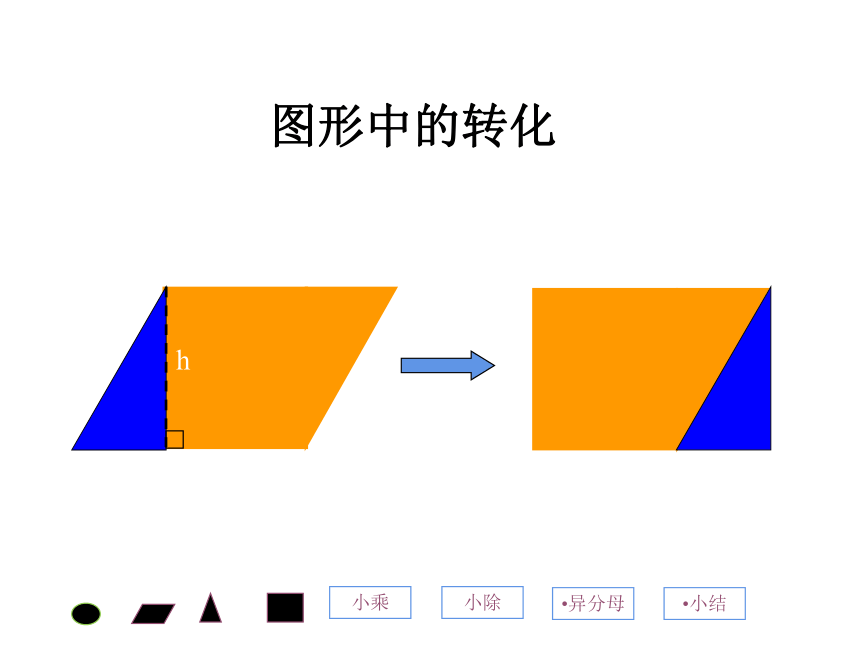
图形中的转化
a
h
a
h
小乘
小除
小结
异分母
a
h
h
a
a
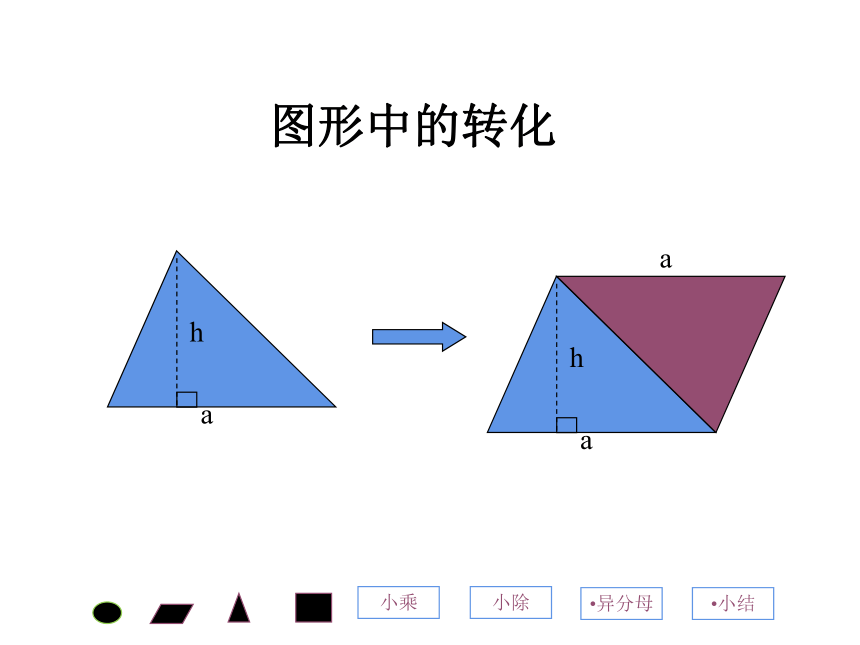
图形中的转化
小乘
小除
小结
异分母
a
h
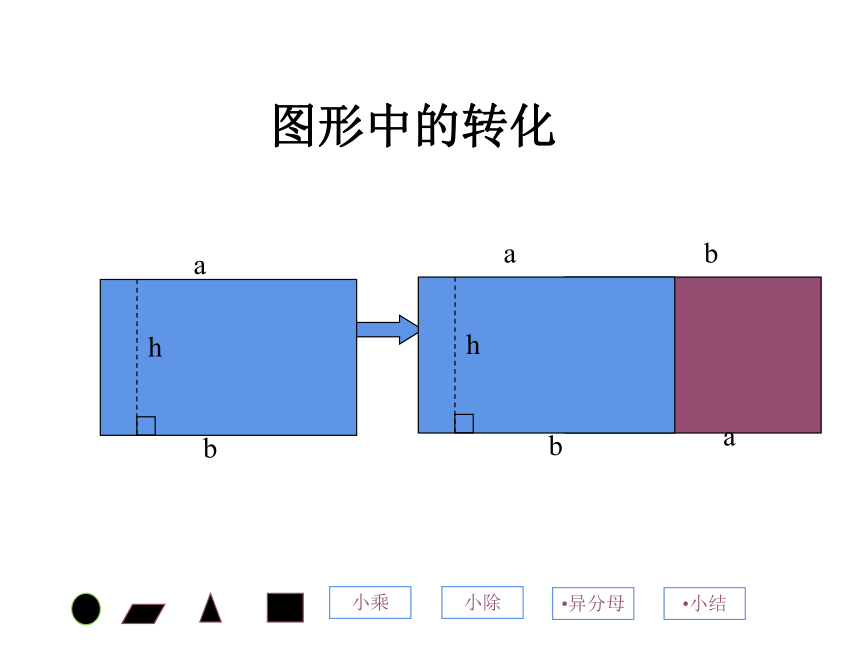
b
a
h
a
b
b
图形中的转化
小乘
小除
小结
异分母
图形中的转化
小乘
小除
小结
异分母
小 数 乘 法
计算中的转化
小结
小乘
小除
异分母
整 数 乘 法
除数是小数的除法
计算中的转化
小乘
小除
小结
异分母
除数是整数的除法
异分母分数加减法
计算中的转化
小结
小乘
小除
异分母
同分母分数加减法
转化
……
小 数 乘 法
整 数 乘 法
除数是小数的除法
除数是整数的除法
异分母分数加减法
同分母分数加减法
未知
已知
仔细观察下面这个图形,要求下面图形的周长,
怎样计算比较简便?
(5+3) ×2=16(厘米)
应用策略
如果每个小方格的边长是1厘米,
这个图形的周长是多少厘米
比一比:
这个图形在转化前后,什么变了?什么没变?
形状变了
应用策略
周长不变
(5+3) ×2=16(厘米)
应用策略
周长不变
面积不变
……
形状变了
形状变了
……
用分数表示各图中的涂色部分。
( )
( )
( )
( )
( )
( )
应用策略
用分数表示各图中的涂色部分。
应用策略
用分数表示各图中的涂色部分。
应用策略
应用策略
应用策略
为什么要转化?(作用)
怎样实现转化?(方法)
转化时要注意什么?(规则)
求下面涂色部分的周长和面积。
33cm
22cm
33cm
22cm
1cm
1cm
33cm
22cm
1cm
1cm
1cm
1cm
分别求出下面图形涂色部分的周长和空白部分面积。
应用策略
47cm
23cm
5cm
3cm
(47+23)×2
=70×2
=140(cm)
42cm
20cm
(47-5)×(23-3)
=42×20
=840( )
33cm
22cm
求下面涂色部分的周长和面积。
1cm
(33+22)×2
=55×2
=110( cm)
33cm
22cm
(33-1)×1+22×1
=32+22
=54( )
1cm
一块草坪被4条1米宽的小路平均分成9小块。草坪的面积是多少平方米?
(45-2)×(27-2)
=43×25
=1075(平方米)
答:草坪的面积是1075平方米?
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
应用策略
1、观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米
(5+3) ×2=16(厘米)
形状变了
应用策略
周长不变
解决问题的策略
苏教版《义务教育教科书 数学》
五年级下册
下面两个图形,哪个面积大一些?
认真观察图形的特点,想一想可以怎样转化
动手试一试。
学习策略
图1:
学习策略
把上面的半圆向下平移8格,正好拼成长方形。
把下面的部分向上平移8格,正好拼成长方形。
图2:
把2个半圆
分别旋转180 ,拼成长方形。
学习策略
图2:
把上面部分一分为二分别旋转180 ,拼成长方形。
学习策略
学习策略
6
8
4
12
转化
形状变了
面积不变
学习策略
图1
图2
我们曾经用转化的策略解决过哪些问题?
小乘
小除
异分母
图形中的转化
a
h
a
h
小乘
小除
小结
异分母
a
h
h
a
a
图形中的转化
小乘
小除
小结
异分母
a
h
b
a
h
a
b
b
图形中的转化
小乘
小除
小结
异分母
图形中的转化
小乘
小除
小结
异分母
小 数 乘 法
计算中的转化
小结
小乘
小除
异分母
整 数 乘 法
除数是小数的除法
计算中的转化
小乘
小除
小结
异分母
除数是整数的除法
异分母分数加减法
计算中的转化
小结
小乘
小除
异分母
同分母分数加减法
转化
……
小 数 乘 法
整 数 乘 法
除数是小数的除法
除数是整数的除法
异分母分数加减法
同分母分数加减法
未知
已知
仔细观察下面这个图形,要求下面图形的周长,
怎样计算比较简便?
(5+3) ×2=16(厘米)
应用策略
如果每个小方格的边长是1厘米,
这个图形的周长是多少厘米
比一比:
这个图形在转化前后,什么变了?什么没变?
形状变了
应用策略
周长不变
(5+3) ×2=16(厘米)
应用策略
周长不变
面积不变
……
形状变了
形状变了
……
用分数表示各图中的涂色部分。
( )
( )
( )
( )
( )
( )
应用策略
用分数表示各图中的涂色部分。
应用策略
用分数表示各图中的涂色部分。
应用策略
应用策略
应用策略
为什么要转化?(作用)
怎样实现转化?(方法)
转化时要注意什么?(规则)
求下面涂色部分的周长和面积。
33cm
22cm
33cm
22cm
1cm
1cm
33cm
22cm
1cm
1cm
1cm
1cm
分别求出下面图形涂色部分的周长和空白部分面积。
应用策略
47cm
23cm
5cm
3cm
(47+23)×2
=70×2
=140(cm)
42cm
20cm
(47-5)×(23-3)
=42×20
=840( )
33cm
22cm
求下面涂色部分的周长和面积。
1cm
(33+22)×2
=55×2
=110( cm)
33cm
22cm
(33-1)×1+22×1
=32+22
=54( )
1cm
一块草坪被4条1米宽的小路平均分成9小块。草坪的面积是多少平方米?
(45-2)×(27-2)
=43×25
=1075(平方米)
答:草坪的面积是1075平方米?
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
应用策略
1、观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米
(5+3) ×2=16(厘米)
形状变了
应用策略
周长不变
