苏科版七年级下册第七章平面图形的认识(二)同位角、内错角、同旁内角的概念 专题练习(word版无答案)
文档属性
| 名称 | 苏科版七年级下册第七章平面图形的认识(二)同位角、内错角、同旁内角的概念 专题练习(word版无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 00:00:00 | ||
图片预览



文档简介
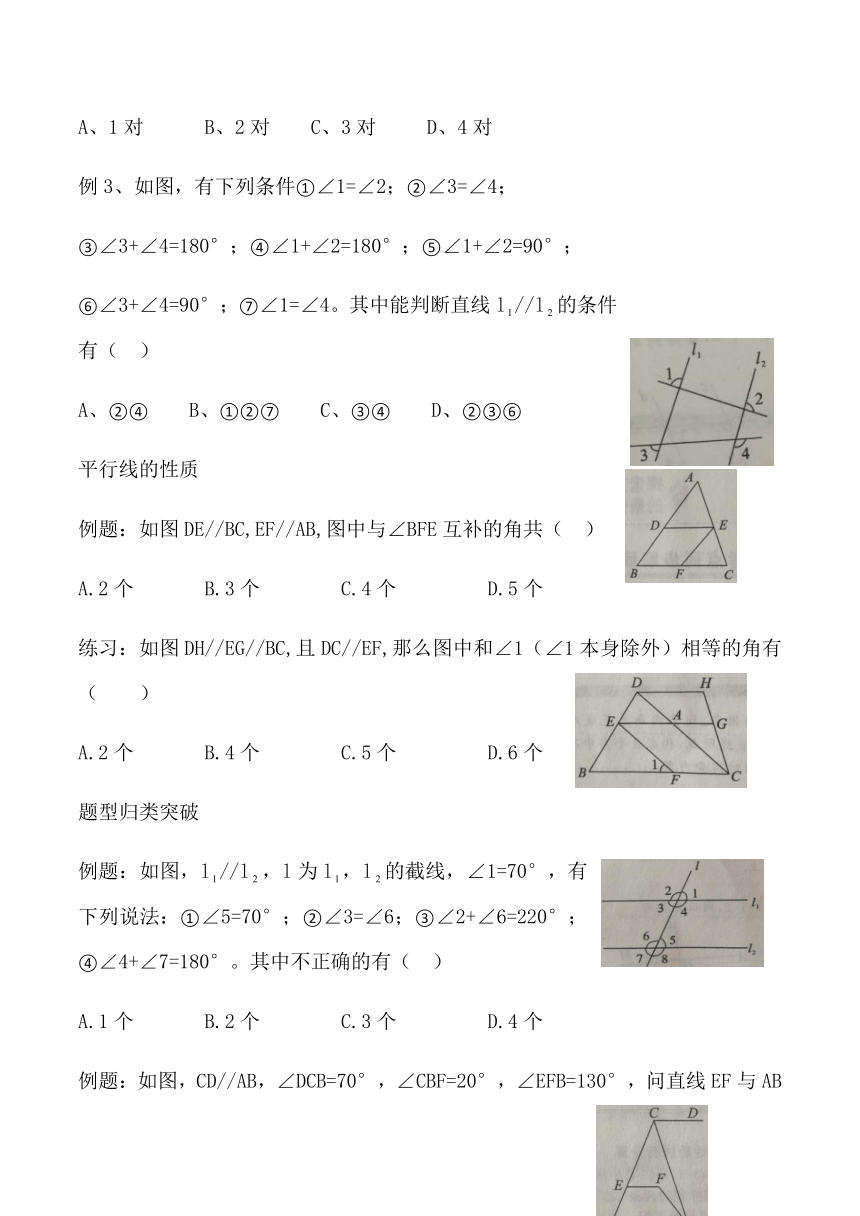
第七章:平面图形的认识(二)
同位角、内错角、同旁内角的概念
如图,下面结论正确的是( )
∠1和∠2是同位角 B、∠2和∠3是内错角
∠2和∠4是同旁内角 D、∠1和∠3是内错角
练习:如图,同位角共有( )
A、6对 B、8对 C、10对 D、12对
如图,要得到a//b,则需要条件( )
∠2=∠4 B、∠1+∠3=180°
C、∠1+∠2=180° D、∠2=∠3
练习:如图,下列说法中,正确的是( )
因为∠2=∠4,所以AD//BC
因为∠BAD+∠D=180°,所以AD//BC
因为∠1=∠3,所以AB//CD
因为∠BAD+∠B=180°,所以AD//BC
题型归类突破
例题1、如图,直线DE截,AB,AC,其中内错角有( )
A、1对 B、2对 C、3对 D、4对
如图,有下列条件①∠1=∠2;②∠3=∠4;
③∠3+∠4=180°;④∠1+∠2=180°;⑤∠1+∠2=90°;
⑥∠3+∠4=90°;⑦∠1=∠4。其中能判断直线l//l的条件有( )
②④ B、①②⑦ C、③④ D、②③⑥
平行线的性质
例题:如图DE//BC,EF//AB,图中与∠BFE互补的角共( )
A.2个 B.3个 C.4个 D.5个
练习:如图DH//EG//BC,且DC//EF,那么图中和∠1(∠1本身除外)相等的角有( )
A.2个 B.4个 C.5个 D.6个
题型归类突破
例题:如图,l//l,l为l,l的截线,∠1=70°,有下列说法:①∠5=70°;②∠3=∠6;③∠2+∠6=220°;④∠4+∠7=180°。其中不正确的有( )
A.1个 B.2个 C.3个 D.4个
例题:如图,CD//AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系?为什么?
图形的平移
例题:下列运动形式:①农村水井打水时水桶的升降;②立式电梯中人的升降;③汽车在平直的公路上行驶;④钟表上指针的运动;⑤电风扇叶片的转动。其中不是平移的有( )
①② B. ②③ C.④⑤ D.①④⑤
练习:下列运动属于平移的是( )
冷水加热过程中小气泡上升成为大气泡
急刹车时汽车在地面上的滑动
C.投篮时的篮球运动
D.随风飘动的树叶在空中的运动
例题:将长度为3㎝的线段向上平移20㎝,所得线段的长度是( )
A.3㎝ B. 23㎝ C.20㎝ D.17㎝
练习:如图,在△ABC中,AB=8㎝,BC=6㎝,AC=7㎝,沿着与AB垂直的方向把△ABC向上平移8㎝,得到△DEF,则阴影部分的面积为
例题:如图,在图形A到图形B的变换过程中,下列描述正确的是( )
A.向下平移2个单位,向右平移4个单位
B.向下平移1个单位,向右平移4个单位
C.向下平移1个单位,向右平移8个单位
D.向下平移2个单位,向右平移8个单位
练习:将图形A向右平移3个单位得到图形B,再将图形B向左平移5个单位得到图形C。如果直接将图形A平移到图形C,则平移的方向和距离是( )
向右、2个单位 B.向右、8个单位
向左、8个单位 D.向左、2个单位
例题:如图,经过平移,△ABC的顶点A移到了点D,请作出平移后的三角形。
例题:如图,某住宅小区内有一矩形地块,想在矩形地块内修筑同样宽的两条“之”字路,余下部分绿化,道路的宽为2m,求绿化的面积。
三角形分类:
例题:下列说法正确的是( )
①等腰三角形是等边三角形。②三角形按边分可以分类为等腰三角形、等边三角形和不等边三角形。③等腰三角形至少有两条边相等。④三角形按角分类可分为锐角三角形、直角三角形和钝角三角形。
A.①② B.① ③④ C.③④ D.①②④
练习:下列说法正确的是( )
等腰三角形肯定是等边三角形 B.由三条线段组成的图形叫三角形
C.锐角三角形中最大的内角一定小于90°
D. 若一个三角形中有一个锐角,则这个三角形是锐角三角形。
例题:已知三角形的两边长分别为4㎝和9cm,则下列长度的四条线段中能作为第三边的是( )
13cm B.6cm C.5cm D.4cm
练习:现有2cm,4cm,6cm,8cm长的四根木棒,任意选取三根组成一个三角形,那么可以组成三角形的个数为( )
A.1 B.2 C.3 D.4
例题:下列说法中错误的是( )
A.三角形三条角平分线都在三角形的内部 B.三角形三条中线都在三角形的内部
C.三角形三条高都在三角形内部 D.三角形三条高至少有一条在三角形的内部
练习:如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )
锐角三角形 B.钝角三角形 C.直角三角形 D.都有可能
题型突破
例题:如图,第1个图中有1个三角形,第2个图中共有5个三角形,第3 个图中共有9个三角形,以此类推,则第6个图中共有三角形 个。
例题:把三角形的面积分为相等的两部分的是( )
三角形的角平分线 B.三角形的中线 C. 三角形的高 D.以上都不对
三角形内角和
例题:在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数。
练习:若△ABC中,∠A:∠B:∠C=2:3:4,则△ABC是 三角形(按角分)
例题:已知两个多边形的内角总和是900°且边数之比为1:2,求这两个多边形的边数。
练习:多边形的每个内角都是156°,则它的边数是( )
10 B. 13 C.15 D.19
例题:如果一个多边形的内角和等于外角和的2倍,那么这个多边形的边数n=
练习:如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°……这样一直走下去,他第一次回到出发点A时,一共走了 m。
题型归类突破
例题:如果一个三角形的三个内角的度数之比为2:3:5,那么这个三角形是( )
锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
例题:若一个n边形n个内角与某一个外角的总和为1350°,则n等于( )
6 B. 7 C. 8 D. 9
例题:若一个多边形外角和与内角和相等,则这个多边形是( )边形。
例题:两个角的两边分别平行,其中一个角是60°,则另一个角是( )
60° B. 120° C.60°或120° D.无法确定
例题:一个多边形的内角和是它的外角和的4倍,求这个多边形的边数。
例题:手工制作课上,老师先将一张矩形纸片折叠成如图所示的形状,若折痕EF与一条边BC的夹角∠EFB=50°,求∠EGF。
同位角、内错角、同旁内角的概念
如图,下面结论正确的是( )
∠1和∠2是同位角 B、∠2和∠3是内错角
∠2和∠4是同旁内角 D、∠1和∠3是内错角
练习:如图,同位角共有( )
A、6对 B、8对 C、10对 D、12对
如图,要得到a//b,则需要条件( )
∠2=∠4 B、∠1+∠3=180°
C、∠1+∠2=180° D、∠2=∠3
练习:如图,下列说法中,正确的是( )
因为∠2=∠4,所以AD//BC
因为∠BAD+∠D=180°,所以AD//BC
因为∠1=∠3,所以AB//CD
因为∠BAD+∠B=180°,所以AD//BC
题型归类突破
例题1、如图,直线DE截,AB,AC,其中内错角有( )
A、1对 B、2对 C、3对 D、4对
如图,有下列条件①∠1=∠2;②∠3=∠4;
③∠3+∠4=180°;④∠1+∠2=180°;⑤∠1+∠2=90°;
⑥∠3+∠4=90°;⑦∠1=∠4。其中能判断直线l//l的条件有( )
②④ B、①②⑦ C、③④ D、②③⑥
平行线的性质
例题:如图DE//BC,EF//AB,图中与∠BFE互补的角共( )
A.2个 B.3个 C.4个 D.5个
练习:如图DH//EG//BC,且DC//EF,那么图中和∠1(∠1本身除外)相等的角有( )
A.2个 B.4个 C.5个 D.6个
题型归类突破
例题:如图,l//l,l为l,l的截线,∠1=70°,有下列说法:①∠5=70°;②∠3=∠6;③∠2+∠6=220°;④∠4+∠7=180°。其中不正确的有( )
A.1个 B.2个 C.3个 D.4个
例题:如图,CD//AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系?为什么?
图形的平移
例题:下列运动形式:①农村水井打水时水桶的升降;②立式电梯中人的升降;③汽车在平直的公路上行驶;④钟表上指针的运动;⑤电风扇叶片的转动。其中不是平移的有( )
①② B. ②③ C.④⑤ D.①④⑤
练习:下列运动属于平移的是( )
冷水加热过程中小气泡上升成为大气泡
急刹车时汽车在地面上的滑动
C.投篮时的篮球运动
D.随风飘动的树叶在空中的运动
例题:将长度为3㎝的线段向上平移20㎝,所得线段的长度是( )
A.3㎝ B. 23㎝ C.20㎝ D.17㎝
练习:如图,在△ABC中,AB=8㎝,BC=6㎝,AC=7㎝,沿着与AB垂直的方向把△ABC向上平移8㎝,得到△DEF,则阴影部分的面积为
例题:如图,在图形A到图形B的变换过程中,下列描述正确的是( )
A.向下平移2个单位,向右平移4个单位
B.向下平移1个单位,向右平移4个单位
C.向下平移1个单位,向右平移8个单位
D.向下平移2个单位,向右平移8个单位
练习:将图形A向右平移3个单位得到图形B,再将图形B向左平移5个单位得到图形C。如果直接将图形A平移到图形C,则平移的方向和距离是( )
向右、2个单位 B.向右、8个单位
向左、8个单位 D.向左、2个单位
例题:如图,经过平移,△ABC的顶点A移到了点D,请作出平移后的三角形。
例题:如图,某住宅小区内有一矩形地块,想在矩形地块内修筑同样宽的两条“之”字路,余下部分绿化,道路的宽为2m,求绿化的面积。
三角形分类:
例题:下列说法正确的是( )
①等腰三角形是等边三角形。②三角形按边分可以分类为等腰三角形、等边三角形和不等边三角形。③等腰三角形至少有两条边相等。④三角形按角分类可分为锐角三角形、直角三角形和钝角三角形。
A.①② B.① ③④ C.③④ D.①②④
练习:下列说法正确的是( )
等腰三角形肯定是等边三角形 B.由三条线段组成的图形叫三角形
C.锐角三角形中最大的内角一定小于90°
D. 若一个三角形中有一个锐角,则这个三角形是锐角三角形。
例题:已知三角形的两边长分别为4㎝和9cm,则下列长度的四条线段中能作为第三边的是( )
13cm B.6cm C.5cm D.4cm
练习:现有2cm,4cm,6cm,8cm长的四根木棒,任意选取三根组成一个三角形,那么可以组成三角形的个数为( )
A.1 B.2 C.3 D.4
例题:下列说法中错误的是( )
A.三角形三条角平分线都在三角形的内部 B.三角形三条中线都在三角形的内部
C.三角形三条高都在三角形内部 D.三角形三条高至少有一条在三角形的内部
练习:如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )
锐角三角形 B.钝角三角形 C.直角三角形 D.都有可能
题型突破
例题:如图,第1个图中有1个三角形,第2个图中共有5个三角形,第3 个图中共有9个三角形,以此类推,则第6个图中共有三角形 个。
例题:把三角形的面积分为相等的两部分的是( )
三角形的角平分线 B.三角形的中线 C. 三角形的高 D.以上都不对
三角形内角和
例题:在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数。
练习:若△ABC中,∠A:∠B:∠C=2:3:4,则△ABC是 三角形(按角分)
例题:已知两个多边形的内角总和是900°且边数之比为1:2,求这两个多边形的边数。
练习:多边形的每个内角都是156°,则它的边数是( )
10 B. 13 C.15 D.19
例题:如果一个多边形的内角和等于外角和的2倍,那么这个多边形的边数n=
练习:如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°……这样一直走下去,他第一次回到出发点A时,一共走了 m。
题型归类突破
例题:如果一个三角形的三个内角的度数之比为2:3:5,那么这个三角形是( )
锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
例题:若一个n边形n个内角与某一个外角的总和为1350°,则n等于( )
6 B. 7 C. 8 D. 9
例题:若一个多边形外角和与内角和相等,则这个多边形是( )边形。
例题:两个角的两边分别平行,其中一个角是60°,则另一个角是( )
60° B. 120° C.60°或120° D.无法确定
例题:一个多边形的内角和是它的外角和的4倍,求这个多边形的边数。
例题:手工制作课上,老师先将一张矩形纸片折叠成如图所示的形状,若折痕EF与一条边BC的夹角∠EFB=50°,求∠EGF。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
