1.4.3 正切函数的图象和性质课件
文档属性
| 名称 | 1.4.3 正切函数的图象和性质课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 356.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-30 00:00:00 | ||
图片预览




文档简介
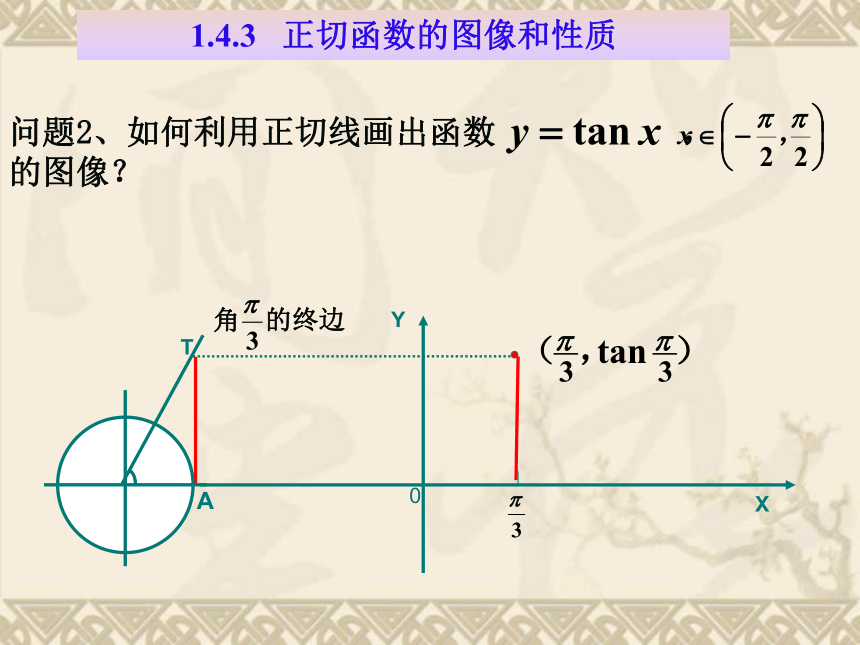
课件23张PPT。1 .4 .3正切函数的图象和性质
湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
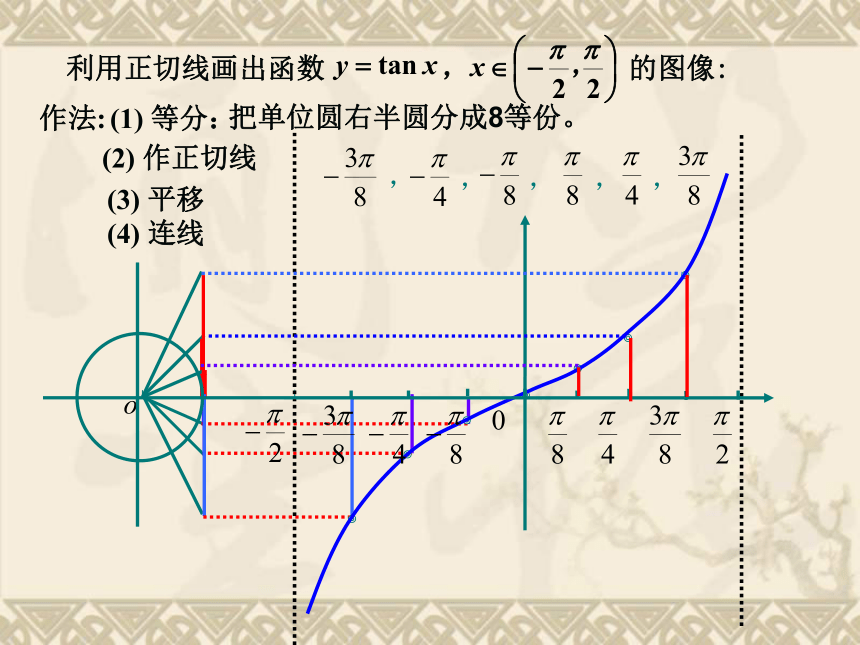
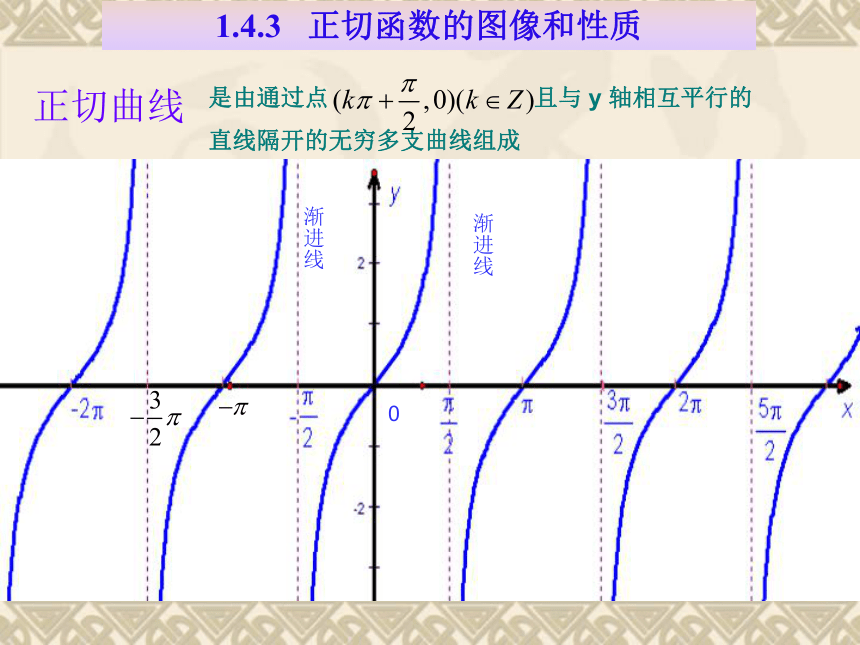
问题提出1.正、余弦函数的图象是通过什么方法作出的? 2.正、余弦函数的基本性质包括哪些内容?这些性质是怎样得到的?3.三角函数包括正、余弦函数和正切函数,我们已经研究了正、余弦函数的图象和性质, 因此, 进一步研究正切函数的性质与图象就成为学习的必然. 一、引入如何用正弦线作正弦函数图象呢?用正切线作正切函数y=tanx的图象1.4.3 正切函数的图像和性质问题1、正切函数 是否为周期函数? ∴ 是周期函数, 是它的一个周期. 我们先来作一个周期内的图象。想一想:先作哪个区间上的图象好呢?利用正切线画出函数 , 的图像: 为什么?二、探究用正切线作正切函数图象1.4.3 正切函数的图像和性质1.4.3 正切函数的图像和性质问题2、如何利用正切线画出函数 , 的图像? 作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。利用正切线画出函数 , 的图像: 正切曲线0是由通过点 且与 y 轴相互平行的
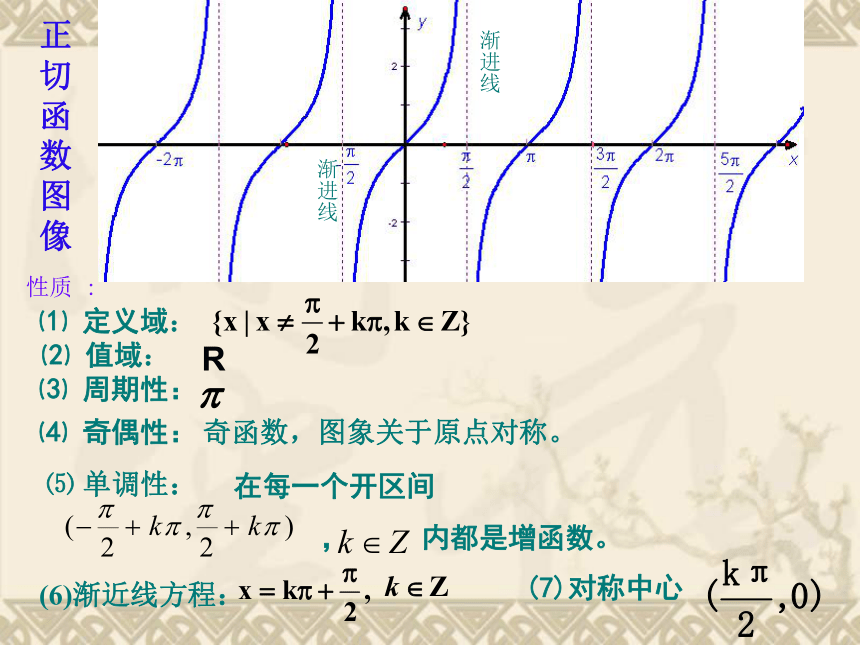
直线隔开的无穷多支曲线组成1.4.3 正切函数的图像和性质⑴ 定义域:⑵ 值域:⑶ 周期性:⑷ 奇偶性: 在每一个开区间
, 内都是增函数。正
切
函
数
图
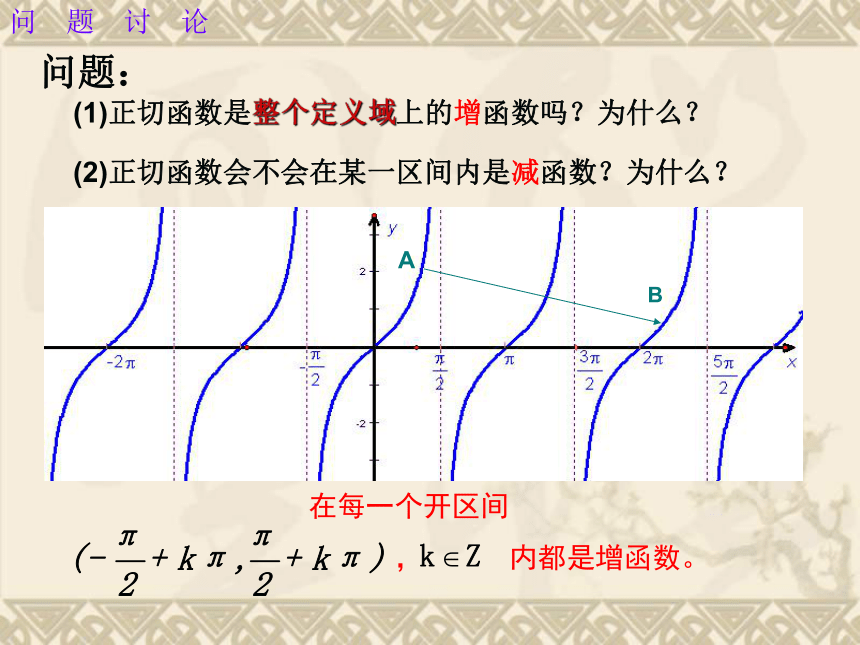
像奇函数,图象关于原点对称。R⑸ 单调性:(6)渐近线方程: (7)对称中心渐进线性质 :渐进线(1)正切函数是整个定义域上的增函数吗?为什么?(2)正切函数会不会在某一区间内是减函数?为什么? 问题: 在每一个开区间
, 内都是增函数。问 题 讨 论A 是奇函数
B 在整个定义域上是增函数
C 在定义域内无最大值和最小值
D 平行于 轴的的直线被正切曲线各支所截线段相等
1.关于正切函数 , 下列判断不正确的是( )2.函数 的一个对称中心是( )A . B. C. D. 基础练习BC例1、比较下列每组数的大小。例题分析解: (1)(2) 例2 求函数 的定义域、周期和单调区间. 解:函数的自变量x应滿足所以,函数的定义域是因此,函数的周期为2因此,函数的单调区间是即由于<x<由 解得<>2、求函数y=tan3x的定义域,值域,单调增区间。反馈演练求函数 的定义域、值域,并指出它的
单调性、奇偶性和周期性;提高练习答案:求函数 的周期.这说明自变量 x ,至少要增加 ,函数的值才能重复取得,所以函数 的周期
是 例3反馈练习:求下列函数的周期:例题分析解:结论:y=Atan(ωx+φ) 周期为T=π/ ω 解:由于f(x)以2为最小正周期,所以对任意x∈R,有f(x+2)=f(x).于是:f(3)=f(1+2)=f(1)=(1-1)2 =0. 2.当x∈(-π,π)时,原函数图象与直线y=4至少有2008个交点,求ω的取值范围.参考答案:(1) 函数的单调区间是(-1+3k,2+3k),k∈Z;(2) ω的取值范围是ω≥1004.解:例题分析例 4解:例 4例题分析反馈演练答案: 1. 2.3. 1. 已知 则( ) A.a , 内都是增函数。奇函数,图象关于原点对称。R(6)单调性:(7)渐近线方程: (5) 对称性:对称中心: 无对称轴 作 业
P45 练习 T2,3,4,6.思考 若 ,求x的取值范围.
湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
问题提出1.正、余弦函数的图象是通过什么方法作出的? 2.正、余弦函数的基本性质包括哪些内容?这些性质是怎样得到的?3.三角函数包括正、余弦函数和正切函数,我们已经研究了正、余弦函数的图象和性质, 因此, 进一步研究正切函数的性质与图象就成为学习的必然. 一、引入如何用正弦线作正弦函数图象呢?用正切线作正切函数y=tanx的图象1.4.3 正切函数的图像和性质问题1、正切函数 是否为周期函数? ∴ 是周期函数, 是它的一个周期. 我们先来作一个周期内的图象。想一想:先作哪个区间上的图象好呢?利用正切线画出函数 , 的图像: 为什么?二、探究用正切线作正切函数图象1.4.3 正切函数的图像和性质1.4.3 正切函数的图像和性质问题2、如何利用正切线画出函数 , 的图像? 作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。利用正切线画出函数 , 的图像: 正切曲线0是由通过点 且与 y 轴相互平行的
直线隔开的无穷多支曲线组成1.4.3 正切函数的图像和性质⑴ 定义域:⑵ 值域:⑶ 周期性:⑷ 奇偶性: 在每一个开区间
, 内都是增函数。正
切
函
数
图
像奇函数,图象关于原点对称。R⑸ 单调性:(6)渐近线方程: (7)对称中心渐进线性质 :渐进线(1)正切函数是整个定义域上的增函数吗?为什么?(2)正切函数会不会在某一区间内是减函数?为什么? 问题: 在每一个开区间
, 内都是增函数。问 题 讨 论A 是奇函数
B 在整个定义域上是增函数
C 在定义域内无最大值和最小值
D 平行于 轴的的直线被正切曲线各支所截线段相等
1.关于正切函数 , 下列判断不正确的是( )2.函数 的一个对称中心是( )A . B. C. D. 基础练习BC例1、比较下列每组数的大小。例题分析解: (1)(2) 例2 求函数 的定义域、周期和单调区间. 解:函数的自变量x应滿足所以,函数的定义域是因此,函数的周期为2因此,函数的单调区间是即由于<x<由 解得<>2、求函数y=tan3x的定义域,值域,单调增区间。反馈演练求函数 的定义域、值域,并指出它的
单调性、奇偶性和周期性;提高练习答案:求函数 的周期.这说明自变量 x ,至少要增加 ,函数的值才能重复取得,所以函数 的周期
是 例3反馈练习:求下列函数的周期:例题分析解:结论:y=Atan(ωx+φ) 周期为T=π/ ω 解:由于f(x)以2为最小正周期,所以对任意x∈R,有f(x+2)=f(x).于是:f(3)=f(1+2)=f(1)=(1-1)2 =0. 2.当x∈(-π,π)时,原函数图象与直线y=4至少有2008个交点,求ω的取值范围.参考答案:(1) 函数的单调区间是(-1+3k,2+3k),k∈Z;(2) ω的取值范围是ω≥1004.解:例题分析例 4解:例 4例题分析反馈演练答案: 1. 2.3. 1. 已知 则( ) A.a
P45 练习 T2,3,4,6.思考 若 ,求x的取值范围.
