苏科版八年级数学上册《3.2 勾股定理的逆定理》教学设计(表格式)
文档属性
| 名称 | 苏科版八年级数学上册《3.2 勾股定理的逆定理》教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 88.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 20:29:01 | ||
图片预览

文档简介
3.2 勾股定理的逆定理
教学目标 1.会阐述直角三角形的判定条件(勾股定理的逆定理).2.会用直角三角形的判定条件判定一个三角形是直角三角形,探索怎样的数组是“勾股数”,进一步发展学生的说理和简单的推理的意识及能力.3.经历探索一个三角形是直角三角形的条件的过程,发展合情推理能力,体会“形”与“数”的内在联系.
教学重点 掌握“三边a、b、c的长满足a2+b2=c2,那么这个三角形是直角三角形”这一方法进行直角三角形的判定.
教学难点 解勾股数的由来,并能用它来解决一些简单的问题.
教学过程(教师) 学生活动 设计思路
温故而知新我们学习了勾股定理,勾股定理的内容是什么?反过来,一个三角形的两边的平方和等于第三边的平方,这个三角形是什么三角形?猜想一下!猜想是否正确,我们走进数学实验室研究一下。 学生回忆,指名口答学生思考,抢答 为新课作铺垫先提出猜想,激发学生探索问题的兴趣.
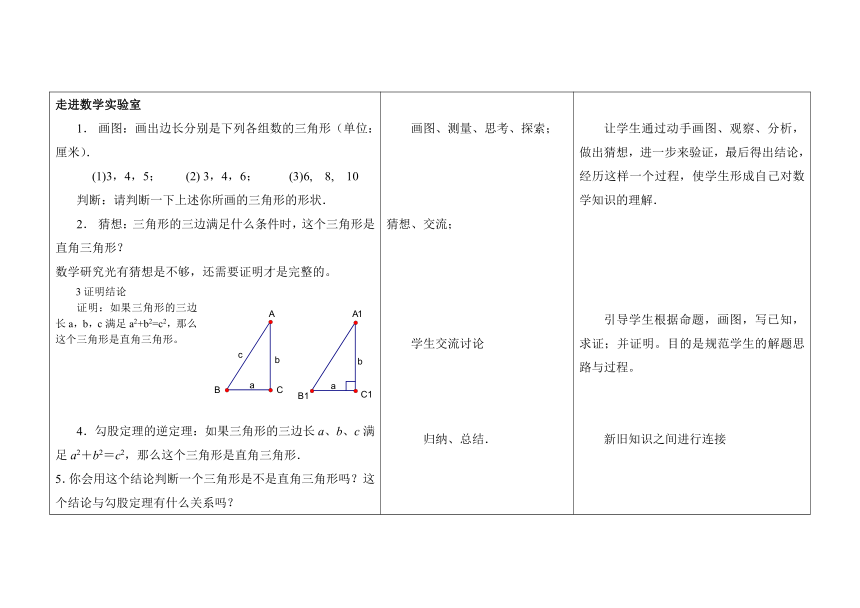
走进数学实验室画图:画出边长分别是下列各组数的三角形(单位:厘米).(1)3,4,5; (2) 3,4,6; (3)6, 8, 10 判断:请判断一下上述你所画的三角形的形状.猜想:三角形的三边满足什么条件时,这个三角形是直角三角形?数学研究光有猜想是不够,还需要证明才是完整的。3证明结论证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。4.勾股定理的逆定理:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.5.你会用这个结论判断一个三角形是不是直角三角形吗?这个结论与勾股定理有什么关系吗? 画图、测量、思考、探索;猜想、交流;学生交流讨论归纳、总结. 让学生通过动手画图、观察、分析,做出猜想,进一步来验证,最后得出结论,经历这样一个过程,使学生形成自己对数学知识的理解.引导学生根据命题,画图,写已知,求证;并证明。目的是规范学生的解题思路与过程。新旧知识之间进行连接
例题解析判断由a,b,c组成的三角形是不是直角三角形。(1)a=15, b=17, c=8 (2)a=7, b=11, c=8抢答1.下列各组数中,不能作为直角三角形的三边的是( )A.3, 4, 5 B.10, 6, 8 C.4, 5, 6 D. 12, 13, 52.若△ABC的两边长为8和15,能使△ABC成为直角三角形的第三边的平方为( )A.161 B.289 C.17 D161或289小试牛刀1.一个三角形的三边分别是6, 7, 8,这个三角形是不是直角三角形?2.一个三角形的三边是12, 16, 20,你能求出这个三角形的面积吗?3.如果一个三角形的三边a,b,c,满足a2=b2-c2,,这个三角形是直角三角形吗?探索规律1.满足a2+b2=c2的3个正整数a、b、c称为勾股数.例如:3、4、5; 6、8、10;是一组勾股数,利用勾股数可以构造直角三角形.除了3、4、5这组勾股数之外,你还能写出其他的勾股数吗?先独立思考,再与同学交流你的结果.2.判断:下列各组数是勾股数吗?(1)6,8,10;(2)9,12,15;(3)12,16,20.你发现什么规律?你还能写出更多的勾股数吗? 思考、分析、规范过程第(2)小题板演抢答交流讨论交流,总结总结规律 检查反馈,巩固所学知识调动学习积极性让学生在快速抢答中,激发好胜心,同时体会数学中的分类思想再次通过一组有梯度的练习,体验成功的快乐。让学生通过观察、分析、验证等过程,发现规律,激发学数学的兴趣,在与他人的交流中获得成功的体验,树立自信心.
例2 已知某校有一块四边形空地ABCD,如图现 计划在该空地上种草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需100元,问需投入多少元? 课堂小结:本节课你有哪些收获?课堂练习课本84-85页练习 1、2、3题. 观察、思考、分析、验证、交流.回想,总结,补充 问题的解决,让学生通过观察,分析,验证等过程,发现规律,激发学数学的兴趣,在与他人的交流中获得成功的体验,树立自信心.由学生总结本节课的内容,再次起到巩固和强调作用。
课后作业习题3.2第1(2)、2题.拓展延伸习题3.2第1(2)题. 思考、分析、完成作业. 感受数学在生活中的应用,增强应用数学的意识.
教学目标 1.会阐述直角三角形的判定条件(勾股定理的逆定理).2.会用直角三角形的判定条件判定一个三角形是直角三角形,探索怎样的数组是“勾股数”,进一步发展学生的说理和简单的推理的意识及能力.3.经历探索一个三角形是直角三角形的条件的过程,发展合情推理能力,体会“形”与“数”的内在联系.
教学重点 掌握“三边a、b、c的长满足a2+b2=c2,那么这个三角形是直角三角形”这一方法进行直角三角形的判定.
教学难点 解勾股数的由来,并能用它来解决一些简单的问题.
教学过程(教师) 学生活动 设计思路
温故而知新我们学习了勾股定理,勾股定理的内容是什么?反过来,一个三角形的两边的平方和等于第三边的平方,这个三角形是什么三角形?猜想一下!猜想是否正确,我们走进数学实验室研究一下。 学生回忆,指名口答学生思考,抢答 为新课作铺垫先提出猜想,激发学生探索问题的兴趣.
走进数学实验室画图:画出边长分别是下列各组数的三角形(单位:厘米).(1)3,4,5; (2) 3,4,6; (3)6, 8, 10 判断:请判断一下上述你所画的三角形的形状.猜想:三角形的三边满足什么条件时,这个三角形是直角三角形?数学研究光有猜想是不够,还需要证明才是完整的。3证明结论证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。4.勾股定理的逆定理:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.5.你会用这个结论判断一个三角形是不是直角三角形吗?这个结论与勾股定理有什么关系吗? 画图、测量、思考、探索;猜想、交流;学生交流讨论归纳、总结. 让学生通过动手画图、观察、分析,做出猜想,进一步来验证,最后得出结论,经历这样一个过程,使学生形成自己对数学知识的理解.引导学生根据命题,画图,写已知,求证;并证明。目的是规范学生的解题思路与过程。新旧知识之间进行连接
例题解析判断由a,b,c组成的三角形是不是直角三角形。(1)a=15, b=17, c=8 (2)a=7, b=11, c=8抢答1.下列各组数中,不能作为直角三角形的三边的是( )A.3, 4, 5 B.10, 6, 8 C.4, 5, 6 D. 12, 13, 52.若△ABC的两边长为8和15,能使△ABC成为直角三角形的第三边的平方为( )A.161 B.289 C.17 D161或289小试牛刀1.一个三角形的三边分别是6, 7, 8,这个三角形是不是直角三角形?2.一个三角形的三边是12, 16, 20,你能求出这个三角形的面积吗?3.如果一个三角形的三边a,b,c,满足a2=b2-c2,,这个三角形是直角三角形吗?探索规律1.满足a2+b2=c2的3个正整数a、b、c称为勾股数.例如:3、4、5; 6、8、10;是一组勾股数,利用勾股数可以构造直角三角形.除了3、4、5这组勾股数之外,你还能写出其他的勾股数吗?先独立思考,再与同学交流你的结果.2.判断:下列各组数是勾股数吗?(1)6,8,10;(2)9,12,15;(3)12,16,20.你发现什么规律?你还能写出更多的勾股数吗? 思考、分析、规范过程第(2)小题板演抢答交流讨论交流,总结总结规律 检查反馈,巩固所学知识调动学习积极性让学生在快速抢答中,激发好胜心,同时体会数学中的分类思想再次通过一组有梯度的练习,体验成功的快乐。让学生通过观察、分析、验证等过程,发现规律,激发学数学的兴趣,在与他人的交流中获得成功的体验,树立自信心.
例2 已知某校有一块四边形空地ABCD,如图现 计划在该空地上种草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需100元,问需投入多少元? 课堂小结:本节课你有哪些收获?课堂练习课本84-85页练习 1、2、3题. 观察、思考、分析、验证、交流.回想,总结,补充 问题的解决,让学生通过观察,分析,验证等过程,发现规律,激发学数学的兴趣,在与他人的交流中获得成功的体验,树立自信心.由学生总结本节课的内容,再次起到巩固和强调作用。
课后作业习题3.2第1(2)、2题.拓展延伸习题3.2第1(2)题. 思考、分析、完成作业. 感受数学在生活中的应用,增强应用数学的意识.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
