北京版八年级数学上册《12.12 勾股定理的逆定理》教学设计(表格式)
文档属性
| 名称 | 北京版八年级数学上册《12.12 勾股定理的逆定理》教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 21:51:15 | ||
图片预览


文档简介
教学基本信息
课题 勾股定理的逆定理
教学目标及重难点
教学目标1.经历实验、观察、猜想、验证、证明、探索勾股定理的逆定理的过程,体验数形结合、从特殊到一般的数学思想. 2.掌握勾股定理的逆定理,对比发现该定理与勾股定理之间的互逆关系,理解三角形三边的等量关系与三角形形状(直角三角形)之间相互影响.3.在探索勾股定理的逆定理的活动中,通过一系列富有探索性的问题,渗透与他人交流、合作的意识和探索精神.教学重难点掌握勾股定理的逆定理,对比发现该定理与勾股定理之间的互逆关系,理解三角形三边的等量关系与三角形形状(直角三角形)之间相互影响.
教学过程
教学阶段 教师活动 学生活动 设置意图 技术应用 时间安排
复习引入 【回忆】如何判定一个三角形为直角三角形,你有什么方法? 预案:1.定义:有一个角是直角的三角形是直角三角形.2.判定方法:有两个锐角互余的三角形是直角三角形.【总结】这两种方法都是从角的角度判定一个三角形为直角三角形的.【思考】能否从三角形三边之间的等量关系判定一个三角形为直角三角形?本节课我们继续学习“直角三角形的判定”.(板书课题) 学生说一说 通过回忆判定三角形为直角三角形的方法引出课题. 课件 2′
创设情境 【问题】大约在公元前2700年,当时的生产工具很落后,测量技术也不是很高明.可是,古埃及人却建成了世界文明的大大小小七十多座金字塔.这些金字塔的塔基都是正方形,其中最大的一座塔基是边长为2300多米的正方形,然而,那时并没有直角三角板,更没有任何先进的测量仪器.这的确是个谜!你能猜出金字塔塔基的正方形的每个直角,古埃及人究竟是怎么确定的吗?要解开这个谜,还是让我们先从一个小实验开始吧.PPT演示:古埃及金字塔,让学生猜测它的塔基可能的形状,教师演示剖开塔基的截面,显示它的形状,正方形的形状得到认同,从而引出本节课探索问题:公元前2700年,古埃及人就已经知道在建筑中应用直角的知识,那么你知道古埃及人究竟是怎么确定直角的吗? 学生思考. 创设情境,使学生产生求知欲,激发学生的兴趣. 课件 3′
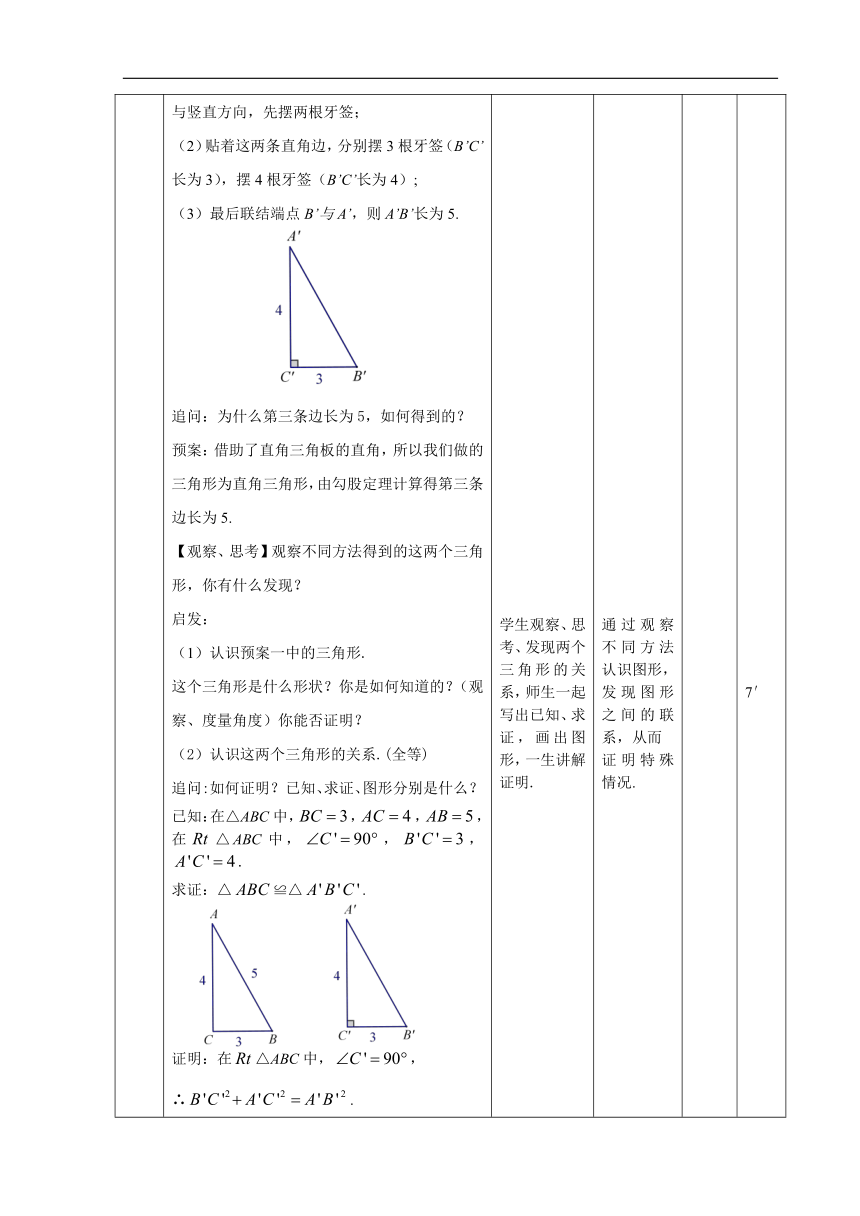
新知探索 (一)动手实验,发现猜想【工具】12根牙签(每根牙签的长为1)、直角三角板、量角器.【任务】用牙签摆一个边长为3、4、5的三角形.【步骤】说一说实验步骤预案一:(1)先摆3根牙签(BC长为3);(2)再顺次摆4根牙签(AC长为4);(3)最后调整位置,摆5根牙签(AB长为5),使得可以组成三角形.预案二:(1)利用直角三角形的两条直角边,沿着水平与竖直方向,先摆两根牙签;(2)贴着这两条直角边,分别摆3根牙签(B’C’长为3),摆4根牙签(B’C’长为4);(3)最后联结端点B’与A’,则A’B’长为5.追问:为什么第三条边长为5,如何得到的?预案:借助了直角三角板的直角,所以我们做的三角形为直角三角形,由勾股定理计算得第三条边长为5.【观察、思考】观察不同方法得到的这两个三角形,你有什么发现?启发:(1)认识预案一中的三角形.这个三角形是什么形状?你是如何知道的?(观察、度量角度)你能否证明?(2)认识这两个三角形的关系.(全等)追问:如何证明?已知、求证、图形分别是什么? 已知:在△ABC中,,,,在△ABC中,,,.求证:△≌△.证明:在△ABC中,,∴.∵,,∴(勾股定理).在△和△中,∵∴△≌△(SSS).【思考】既然我们已经能够证明这两个三角形全等,那么你能证明△ABC为直角三角形吗?预案:学生利用全等三角形性质证明.教师继续板书.∴.【结论】边长为3、4、5的三角形为直角三角形.【猜想】当一个三角形的三条边满足怎样的等量关系,这个三角形才可能是直角三角形.☆我的猜想: 预案:在一个三角形中,如果两条较短边的平方和等于较长边的平方,那么这个三角形为直角三角形.(二)画板演示、验证猜想【几何画板演示】当边长变为任意正数,且满足较短边的平方和等于较长边的平方,学生观察三角形形状是否发生变化.(三)说理论证、证明猜想【思考】已知:在△ABC中,,,,且.求证:.证明:作△,使,,.∴.∵,∴.∴.在△和△中,∵∴△≌△(SSS).∴.【思考】除了上述构造直角三角形的方法,还可以怎么构造?预案(一):作△,使,,.用勾股定理证明,再证明全等解决问题.预案(二):作△,使,,.用勾股定理证明,再证明全等解决问题.【总结】对比这三种证法都需要构造直角三角形,然后利用全等证明猜想.★(四)语言表述,归纳定理文字语言:在三角形中,如果两条较短边的平方和等于较短边的平方,那么这个三角形为直角三角形.符号语言:在△ABC中,三边为、、.∵,∴.(△ABC为直角三角形)(五)对比发现,理解定理【对比】我们刚才证明的定理与勾股定理有什么区别与联系,给这个定理命名.定理文字语言图形语言符号语言联系勾股定理 定理【思考】这两个定理的作用分别是什么?勾股定理:已知直角三角形两条边的长度计算第三边的长.勾股定理的逆定理:从三边的数量关系判断一个三角形为直角三角形.【总结】无论哪一个定理都说明三角形的形状与三边的等量关系相互影响,与边的长短无关. 学生先独立思考尝试,再组内交流,组间派代表展示.学生观察、思考、发现两个三角形的关系,师生一起写出已知、求证,画出图形,一生讲解证明.学生思考、发现猜想.教师画板演示,学生观察.一生叙述已知、求证.教师启发学生分析辅助线作法,共同作图、讨论、证明.学生代表展示.师生共同归纳定理.学生填表,交流,给定理命名. 通过学生动手操作,观察、分析、猜想,合作交流,人人参与活动,体验并感悟“图形”和“数量”之间的相互联系.通过观察不同方法认识图形,发现图形之间的联系,从而证明特殊情况.由实验的结论学生发现猜想,同时质疑边长改变但是关系不变,三角形的形状是否发生改变.几何画板演示验证猜想,进一步加深学生的感性认识.培养学生学数学的严谨性和科学性,提高他们的逻辑推理能力,使学生活动的兴奋点有动手操作向理性说理转变.通过不同做法的交流,训练学生解题的灵活性,培养学生发散思维.培养学生对于几何定理三种语言的表述能力.通过对比加深对于定理的理解,防止混淆. 学案 5′7′2′2′6′5′3′5′
新知应用 答疑解惑:同学们经过前面的学习,你知道古埃及认识如何确定直角的吗?古埃及人把一根长绳打上等距离的13个结,然后用桩钉如图那样钉成一个三角形,用这种方法确定直角,你知道这是为什么吗? 独立思考、一生解答. 照应开头解开金字塔塔基之谜,巩固定理. 学案 2′
归纳总结 1.通过本节课的学习,一个三角形的三边在数量上满足怎样的关系时,这个三角形是直角三角形?2.判定一个三角形为直角三角形都有哪些方法?3.回顾“勾股定理的逆定理”的探索过程用到什么数学思想? 学生代表总结 培养学生归纳总结能力及解题后的反思能力. 课件 2′
分层作业 基础题:书上第119 页习题12-5基础第3题.综合题:已知:在四边形ABCD中,AB、BC、CD、DA的长分别为2、2、2、2,且AB⊥BC,求∠BAD的度数.提高题:已知:a=m2-n2,b=2mn,c=m2+n2,(m、n为正整数,m>n).试判定由a、b、c组成的三角形是不是直角三角形,为什么? 1.2题必做,3题选作. 通过分层作业,是不同的学生在数学学习上有不同的收获. 学案 1′
PAGE
课题 勾股定理的逆定理
教学目标及重难点
教学目标1.经历实验、观察、猜想、验证、证明、探索勾股定理的逆定理的过程,体验数形结合、从特殊到一般的数学思想. 2.掌握勾股定理的逆定理,对比发现该定理与勾股定理之间的互逆关系,理解三角形三边的等量关系与三角形形状(直角三角形)之间相互影响.3.在探索勾股定理的逆定理的活动中,通过一系列富有探索性的问题,渗透与他人交流、合作的意识和探索精神.教学重难点掌握勾股定理的逆定理,对比发现该定理与勾股定理之间的互逆关系,理解三角形三边的等量关系与三角形形状(直角三角形)之间相互影响.
教学过程
教学阶段 教师活动 学生活动 设置意图 技术应用 时间安排
复习引入 【回忆】如何判定一个三角形为直角三角形,你有什么方法? 预案:1.定义:有一个角是直角的三角形是直角三角形.2.判定方法:有两个锐角互余的三角形是直角三角形.【总结】这两种方法都是从角的角度判定一个三角形为直角三角形的.【思考】能否从三角形三边之间的等量关系判定一个三角形为直角三角形?本节课我们继续学习“直角三角形的判定”.(板书课题) 学生说一说 通过回忆判定三角形为直角三角形的方法引出课题. 课件 2′
创设情境 【问题】大约在公元前2700年,当时的生产工具很落后,测量技术也不是很高明.可是,古埃及人却建成了世界文明的大大小小七十多座金字塔.这些金字塔的塔基都是正方形,其中最大的一座塔基是边长为2300多米的正方形,然而,那时并没有直角三角板,更没有任何先进的测量仪器.这的确是个谜!你能猜出金字塔塔基的正方形的每个直角,古埃及人究竟是怎么确定的吗?要解开这个谜,还是让我们先从一个小实验开始吧.PPT演示:古埃及金字塔,让学生猜测它的塔基可能的形状,教师演示剖开塔基的截面,显示它的形状,正方形的形状得到认同,从而引出本节课探索问题:公元前2700年,古埃及人就已经知道在建筑中应用直角的知识,那么你知道古埃及人究竟是怎么确定直角的吗? 学生思考. 创设情境,使学生产生求知欲,激发学生的兴趣. 课件 3′
新知探索 (一)动手实验,发现猜想【工具】12根牙签(每根牙签的长为1)、直角三角板、量角器.【任务】用牙签摆一个边长为3、4、5的三角形.【步骤】说一说实验步骤预案一:(1)先摆3根牙签(BC长为3);(2)再顺次摆4根牙签(AC长为4);(3)最后调整位置,摆5根牙签(AB长为5),使得可以组成三角形.预案二:(1)利用直角三角形的两条直角边,沿着水平与竖直方向,先摆两根牙签;(2)贴着这两条直角边,分别摆3根牙签(B’C’长为3),摆4根牙签(B’C’长为4);(3)最后联结端点B’与A’,则A’B’长为5.追问:为什么第三条边长为5,如何得到的?预案:借助了直角三角板的直角,所以我们做的三角形为直角三角形,由勾股定理计算得第三条边长为5.【观察、思考】观察不同方法得到的这两个三角形,你有什么发现?启发:(1)认识预案一中的三角形.这个三角形是什么形状?你是如何知道的?(观察、度量角度)你能否证明?(2)认识这两个三角形的关系.(全等)追问:如何证明?已知、求证、图形分别是什么? 已知:在△ABC中,,,,在△ABC中,,,.求证:△≌△.证明:在△ABC中,,∴.∵,,∴(勾股定理).在△和△中,∵∴△≌△(SSS).【思考】既然我们已经能够证明这两个三角形全等,那么你能证明△ABC为直角三角形吗?预案:学生利用全等三角形性质证明.教师继续板书.∴.【结论】边长为3、4、5的三角形为直角三角形.【猜想】当一个三角形的三条边满足怎样的等量关系,这个三角形才可能是直角三角形.☆我的猜想: 预案:在一个三角形中,如果两条较短边的平方和等于较长边的平方,那么这个三角形为直角三角形.(二)画板演示、验证猜想【几何画板演示】当边长变为任意正数,且满足较短边的平方和等于较长边的平方,学生观察三角形形状是否发生变化.(三)说理论证、证明猜想【思考】已知:在△ABC中,,,,且.求证:.证明:作△,使,,.∴.∵,∴.∴.在△和△中,∵∴△≌△(SSS).∴.【思考】除了上述构造直角三角形的方法,还可以怎么构造?预案(一):作△,使,,.用勾股定理证明,再证明全等解决问题.预案(二):作△,使,,.用勾股定理证明,再证明全等解决问题.【总结】对比这三种证法都需要构造直角三角形,然后利用全等证明猜想.★(四)语言表述,归纳定理文字语言:在三角形中,如果两条较短边的平方和等于较短边的平方,那么这个三角形为直角三角形.符号语言:在△ABC中,三边为、、.∵,∴.(△ABC为直角三角形)(五)对比发现,理解定理【对比】我们刚才证明的定理与勾股定理有什么区别与联系,给这个定理命名.定理文字语言图形语言符号语言联系勾股定理 定理【思考】这两个定理的作用分别是什么?勾股定理:已知直角三角形两条边的长度计算第三边的长.勾股定理的逆定理:从三边的数量关系判断一个三角形为直角三角形.【总结】无论哪一个定理都说明三角形的形状与三边的等量关系相互影响,与边的长短无关. 学生先独立思考尝试,再组内交流,组间派代表展示.学生观察、思考、发现两个三角形的关系,师生一起写出已知、求证,画出图形,一生讲解证明.学生思考、发现猜想.教师画板演示,学生观察.一生叙述已知、求证.教师启发学生分析辅助线作法,共同作图、讨论、证明.学生代表展示.师生共同归纳定理.学生填表,交流,给定理命名. 通过学生动手操作,观察、分析、猜想,合作交流,人人参与活动,体验并感悟“图形”和“数量”之间的相互联系.通过观察不同方法认识图形,发现图形之间的联系,从而证明特殊情况.由实验的结论学生发现猜想,同时质疑边长改变但是关系不变,三角形的形状是否发生改变.几何画板演示验证猜想,进一步加深学生的感性认识.培养学生学数学的严谨性和科学性,提高他们的逻辑推理能力,使学生活动的兴奋点有动手操作向理性说理转变.通过不同做法的交流,训练学生解题的灵活性,培养学生发散思维.培养学生对于几何定理三种语言的表述能力.通过对比加深对于定理的理解,防止混淆. 学案 5′7′2′2′6′5′3′5′
新知应用 答疑解惑:同学们经过前面的学习,你知道古埃及认识如何确定直角的吗?古埃及人把一根长绳打上等距离的13个结,然后用桩钉如图那样钉成一个三角形,用这种方法确定直角,你知道这是为什么吗? 独立思考、一生解答. 照应开头解开金字塔塔基之谜,巩固定理. 学案 2′
归纳总结 1.通过本节课的学习,一个三角形的三边在数量上满足怎样的关系时,这个三角形是直角三角形?2.判定一个三角形为直角三角形都有哪些方法?3.回顾“勾股定理的逆定理”的探索过程用到什么数学思想? 学生代表总结 培养学生归纳总结能力及解题后的反思能力. 课件 2′
分层作业 基础题:书上第119 页习题12-5基础第3题.综合题:已知:在四边形ABCD中,AB、BC、CD、DA的长分别为2、2、2、2,且AB⊥BC,求∠BAD的度数.提高题:已知:a=m2-n2,b=2mn,c=m2+n2,(m、n为正整数,m>n).试判定由a、b、c组成的三角形是不是直角三角形,为什么? 1.2题必做,3题选作. 通过分层作业,是不同的学生在数学学习上有不同的收获. 学案 1′
PAGE
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
