北师大版八年级数学下册第六章1. 《平行四边形的边和角的性质》教学设计
文档属性
| 名称 | 北师大版八年级数学下册第六章1. 《平行四边形的边和角的性质》教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 92.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 00:00:00 | ||
图片预览

文档简介
6.1平行四边形的性质(一)
一、教材解读
《6.1平行四边形的性质(一)》是北师大版八年级下第六章第一节第一课时,小学阶段学生对平行四边形已经有所认识,初中在此之前学生已经学习了图形的变换(平移、旋转、轴对称和中心对称),也学会了全等的证明等几何内容。本节课是利用已学的几何知识探索平行四边形的性质,基本的研究思路和方法对后续特殊平行四边形的学习有重要的作用。同时本节课平行四边形的性质在现实生活中也有广泛的应用。
二、学情分析
学生已经有了研究几何的基本经验,也具备了一定的动手操作能力和推理证明能力,本次对平行四边形性质的探索,可仿照三角形探索的经验,从边,角进行探索,借助旋转知识,对对称性和对角线进行探究,因此可以最大限度放手让学生动手进行探究,尝试对探究结果进行说理证明。
三、教学目标
1、知识与技能:掌握平行四边形的定义以及表示方法,理解平行四边形的中心对称性,掌握并能证明平行四边形的对边相等,对角相等,发展学生演绎推理的能力。
2、过程与方法:经历探索平行四边形性质的过程,体验猜想,验证,证明等一系列数学探索研究的过程,掌握研究平行四边形的基本方法,和主要研究方向:对称性,边,角等。通过开放性的同伴出题,在实践操作中掌握平行四边形的性质。
3、情感态度价值观:让学生在动手操作的过程中感受到数学学习的乐趣,让学生相互出题的过程中学会合作学习,学会解决问题,更学会提出问题,培养学生学习数学的良好品质。
教学重难点
掌握平行四边形的定义以及表示方法,理解平行四边形的中心对称性,掌握并能证明平行四边形的对边相等,对角相等,发展学生演绎推理的能力。
四、教学设计
[回顾迎新]
如右上图,平行四边形ABCD可以看成某个基本图形旋转得到吗?如果不可以请说明理由.如果可以,基本图形是_______,旋转中心是___________________,旋转角度为_______度.
[情景引入]
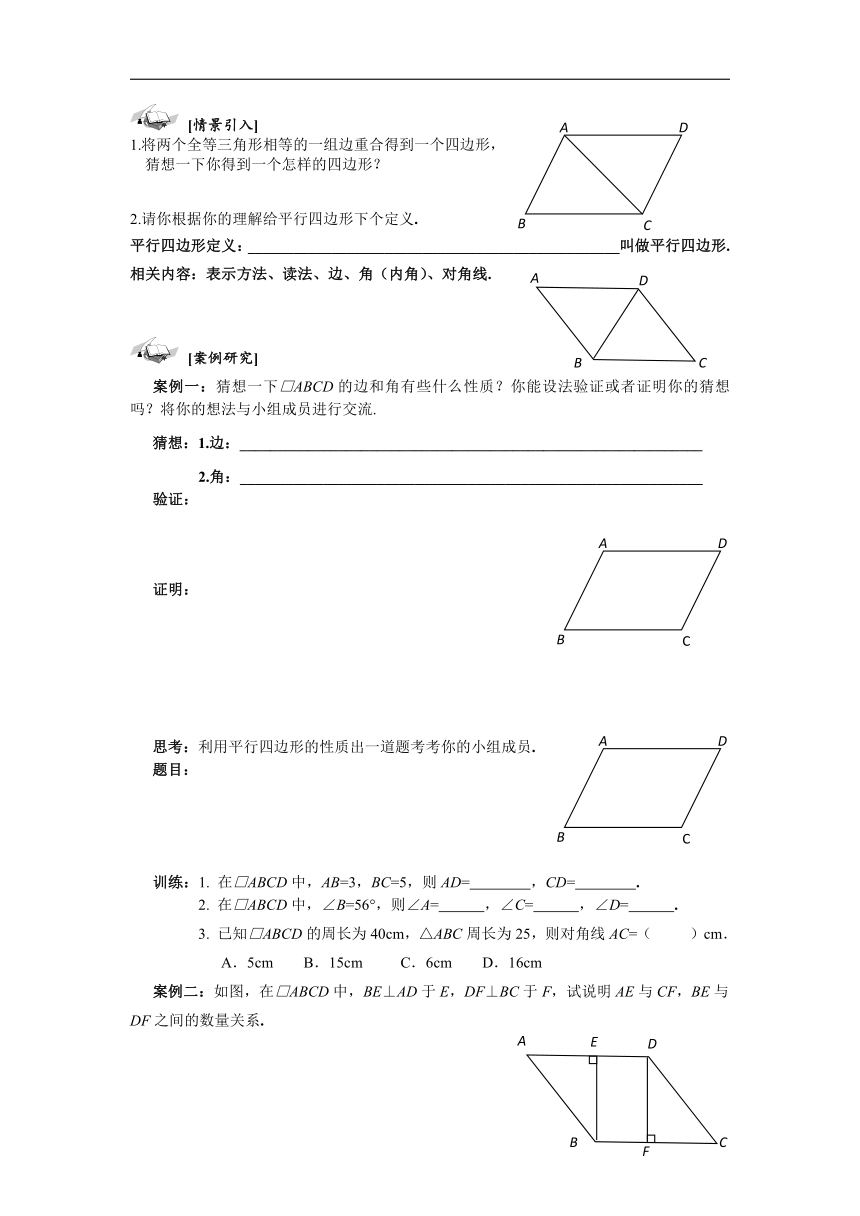
1.将两个全等三角形相等的一组边重合得到一个四边形,
猜想一下你得到一个怎样的四边形?
2.请你根据你的理解给平行四边形下个定义.
平行四边形定义:_________________________________________________叫做平行四边形.
相关内容:表示方法、读法、边、角(内角)、对角线.
[案例研究]
案例一:猜想一下□ABCD的边和角有些什么性质?你能设法验证或者证明你的猜想吗?将你的想法与小组成员进行交流.
猜想:1.边:_____________________________________________________________
2.角:_____________________________________________________________
验证:
证明:
思考:利用平行四边形的性质出一道题考考你的小组成员.
题目:
训练:1. 在□ABCD中,AB=3,BC=5,则AD= ,CD= .
2. 在□ABCD中,∠B=56°,则∠A= ,∠C= ,∠D= .
3. 已知□ABCD的周长为40cm,△ABC周长为25,则对角线AC=( )cm.
A.5cm B.15cm C.6cm D.16cm
案例二:如图,在□ABCD中,BE⊥AD于E,DF⊥BC于F,试说明AE与CF,BE与DF之间的数量关系.
[总结归纳] (对本节课内容的一个总结反思)
[及时强化]
基础题:1.在□ABCD中,A=48°,BC=3,则B= _______,C= _______,BC=_______.
2.如右图,在□ABCD中,ADC=125°,CAD=21°,
则ABC=______, CAB=______.
能力题: 3.在□ABCD中,A: B= 1 : 2 , C=______,D=______.
4.在□ABCD中,A的平分线分BC成4cm和3cm两条线段,□ABCD的周长为_________.
5.如图,在□ABCD中,平行于对角线BD的直线MN分别交CD,CB延长线于M,N,交AD于P,交AB于Q,你能说明MQ=NP吗?说说你的理由.
[学后反思](跟大家分享一下你这节课的收获)
三、课后延伸
[作业布置]《新课标同步训练》平行四边形的性质第1课时;
五、教学反思
1.数学来源于生活
用丰富的图形背景让学生充分感受到数学来源于生活,通过实际探索研究,让学生感受平行四边形知识应用于实际生活,服务于实际生活。感受到学习数学知识的意义和价值。
2.在操作中学习在体验中提升
儿童深层次的认知发展,既需要独立思考,更需要合作交流。现代认知学派认为,在学习过程中,只有经过学习者自己探索和概括的知识,才能真正纳入其自身认知结构,获得深刻的理解,在应用时才易检索。这里的“自己探索和概括”就是独立思考,学生的思维是在自己原有的认知结构上建构的,我尽可能多地给学生充分自主思考的空间和时间,即使他们找不到思路,也充分感知了困难、尝试了困难,为进一步探究奠定了基础。这节课通过拼图,旋转等一系列的操作,让学生直观感受平行四边形的性质,并作出猜想,尝试证明,让学生充分经历知识的发生和形成过程。通过学生互相出题,不仅增强学生的兴趣,充分调动学生的积极性,同时也深化学生对平行四边形性质的认识。
一、教材解读
《6.1平行四边形的性质(一)》是北师大版八年级下第六章第一节第一课时,小学阶段学生对平行四边形已经有所认识,初中在此之前学生已经学习了图形的变换(平移、旋转、轴对称和中心对称),也学会了全等的证明等几何内容。本节课是利用已学的几何知识探索平行四边形的性质,基本的研究思路和方法对后续特殊平行四边形的学习有重要的作用。同时本节课平行四边形的性质在现实生活中也有广泛的应用。
二、学情分析
学生已经有了研究几何的基本经验,也具备了一定的动手操作能力和推理证明能力,本次对平行四边形性质的探索,可仿照三角形探索的经验,从边,角进行探索,借助旋转知识,对对称性和对角线进行探究,因此可以最大限度放手让学生动手进行探究,尝试对探究结果进行说理证明。
三、教学目标
1、知识与技能:掌握平行四边形的定义以及表示方法,理解平行四边形的中心对称性,掌握并能证明平行四边形的对边相等,对角相等,发展学生演绎推理的能力。
2、过程与方法:经历探索平行四边形性质的过程,体验猜想,验证,证明等一系列数学探索研究的过程,掌握研究平行四边形的基本方法,和主要研究方向:对称性,边,角等。通过开放性的同伴出题,在实践操作中掌握平行四边形的性质。
3、情感态度价值观:让学生在动手操作的过程中感受到数学学习的乐趣,让学生相互出题的过程中学会合作学习,学会解决问题,更学会提出问题,培养学生学习数学的良好品质。
教学重难点
掌握平行四边形的定义以及表示方法,理解平行四边形的中心对称性,掌握并能证明平行四边形的对边相等,对角相等,发展学生演绎推理的能力。
四、教学设计
[回顾迎新]
如右上图,平行四边形ABCD可以看成某个基本图形旋转得到吗?如果不可以请说明理由.如果可以,基本图形是_______,旋转中心是___________________,旋转角度为_______度.
[情景引入]
1.将两个全等三角形相等的一组边重合得到一个四边形,
猜想一下你得到一个怎样的四边形?
2.请你根据你的理解给平行四边形下个定义.
平行四边形定义:_________________________________________________叫做平行四边形.
相关内容:表示方法、读法、边、角(内角)、对角线.
[案例研究]
案例一:猜想一下□ABCD的边和角有些什么性质?你能设法验证或者证明你的猜想吗?将你的想法与小组成员进行交流.
猜想:1.边:_____________________________________________________________
2.角:_____________________________________________________________
验证:
证明:
思考:利用平行四边形的性质出一道题考考你的小组成员.
题目:
训练:1. 在□ABCD中,AB=3,BC=5,则AD= ,CD= .
2. 在□ABCD中,∠B=56°,则∠A= ,∠C= ,∠D= .
3. 已知□ABCD的周长为40cm,△ABC周长为25,则对角线AC=( )cm.
A.5cm B.15cm C.6cm D.16cm
案例二:如图,在□ABCD中,BE⊥AD于E,DF⊥BC于F,试说明AE与CF,BE与DF之间的数量关系.
[总结归纳] (对本节课内容的一个总结反思)
[及时强化]
基础题:1.在□ABCD中,A=48°,BC=3,则B= _______,C= _______,BC=_______.
2.如右图,在□ABCD中,ADC=125°,CAD=21°,
则ABC=______, CAB=______.
能力题: 3.在□ABCD中,A: B= 1 : 2 , C=______,D=______.
4.在□ABCD中,A的平分线分BC成4cm和3cm两条线段,□ABCD的周长为_________.
5.如图,在□ABCD中,平行于对角线BD的直线MN分别交CD,CB延长线于M,N,交AD于P,交AB于Q,你能说明MQ=NP吗?说说你的理由.
[学后反思](跟大家分享一下你这节课的收获)
三、课后延伸
[作业布置]《新课标同步训练》平行四边形的性质第1课时;
五、教学反思
1.数学来源于生活
用丰富的图形背景让学生充分感受到数学来源于生活,通过实际探索研究,让学生感受平行四边形知识应用于实际生活,服务于实际生活。感受到学习数学知识的意义和价值。
2.在操作中学习在体验中提升
儿童深层次的认知发展,既需要独立思考,更需要合作交流。现代认知学派认为,在学习过程中,只有经过学习者自己探索和概括的知识,才能真正纳入其自身认知结构,获得深刻的理解,在应用时才易检索。这里的“自己探索和概括”就是独立思考,学生的思维是在自己原有的认知结构上建构的,我尽可能多地给学生充分自主思考的空间和时间,即使他们找不到思路,也充分感知了困难、尝试了困难,为进一步探究奠定了基础。这节课通过拼图,旋转等一系列的操作,让学生直观感受平行四边形的性质,并作出猜想,尝试证明,让学生充分经历知识的发生和形成过程。通过学生互相出题,不仅增强学生的兴趣,充分调动学生的积极性,同时也深化学生对平行四边形性质的认识。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
