青岛版数学八下9.5《解直角三角形的应用》ppt
文档属性
| 名称 | 青岛版数学八下9.5《解直角三角形的应用》ppt |  | |
| 格式 | zip | ||
| 文件大小 | 298.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-01 18:50:14 | ||
图片预览



文档简介
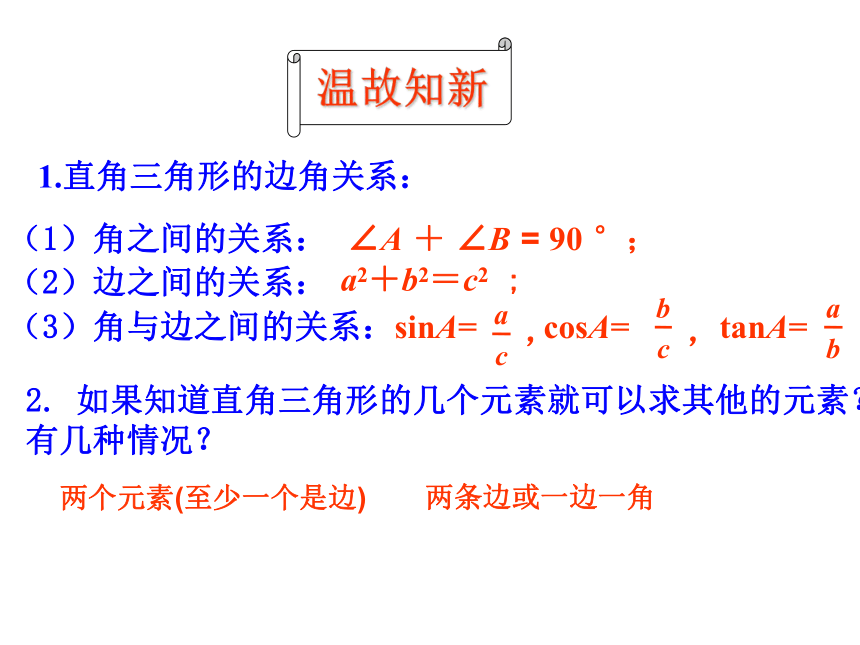
课件14张PPT。§9.5 解直角三角形的应用(1)第9章 解直角三角形∠A + ∠B = 90 °;a2+b2=c2 ; (3)角与边之间的关系:(2)边之间的关系:(1)角之间的关系:2. 如果知道直角三角形的几个元素就可以求其他的元素?
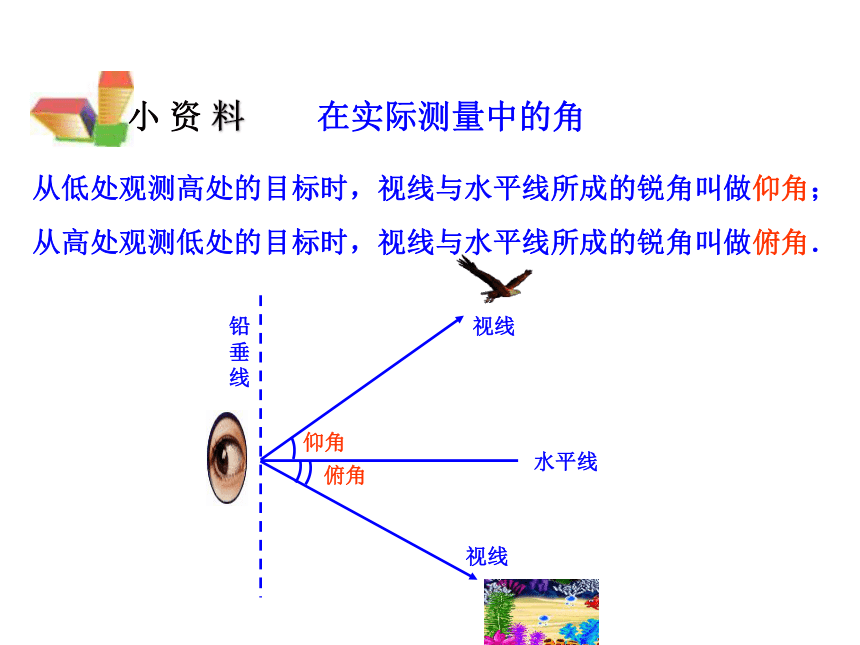
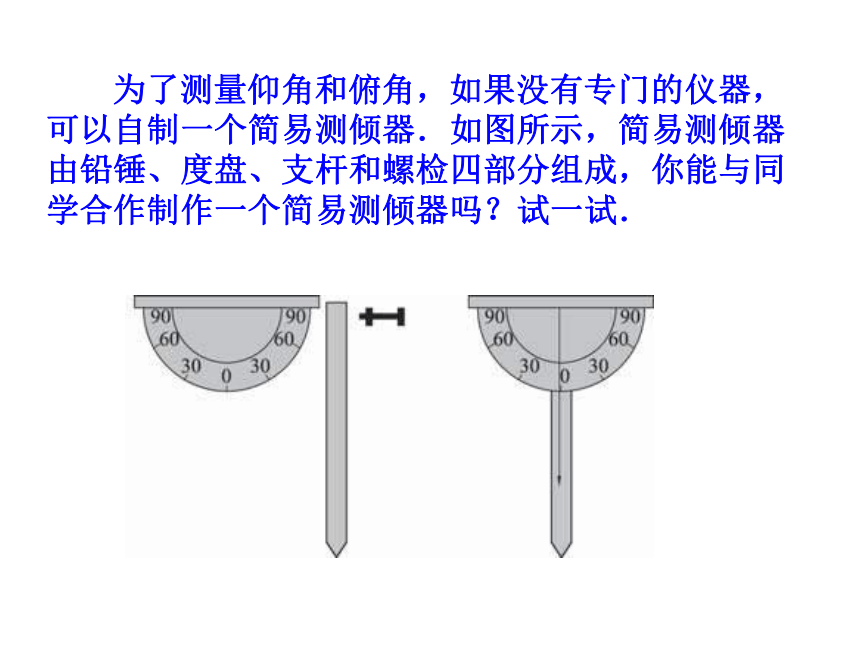
有几种情况?两个元素(至少一个是边)两条边或一边一角1.直角三角形的边角关系:温故知新 上海东方明珠塔于1994 年10 月1 日建成,在各国广播电视塔的排名榜中,当时其高度列亚洲第一、世界第三.与外滩的“万国建筑博览群”隔江相望.在塔顶俯瞰上海风景,美不胜收.运用本章所学过的知识,能测出东方明珠塔的高度来吗? 小 资 料在实际测量中的角从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角; 为了测量仰角和俯角,如果没有专门的仪器,可以自制一个简易测倾器.如图所示,简易测倾器由铅锤、度盘、支杆和螺检四部分组成,你能与同学合作制作一个简易测倾器吗?试一试.
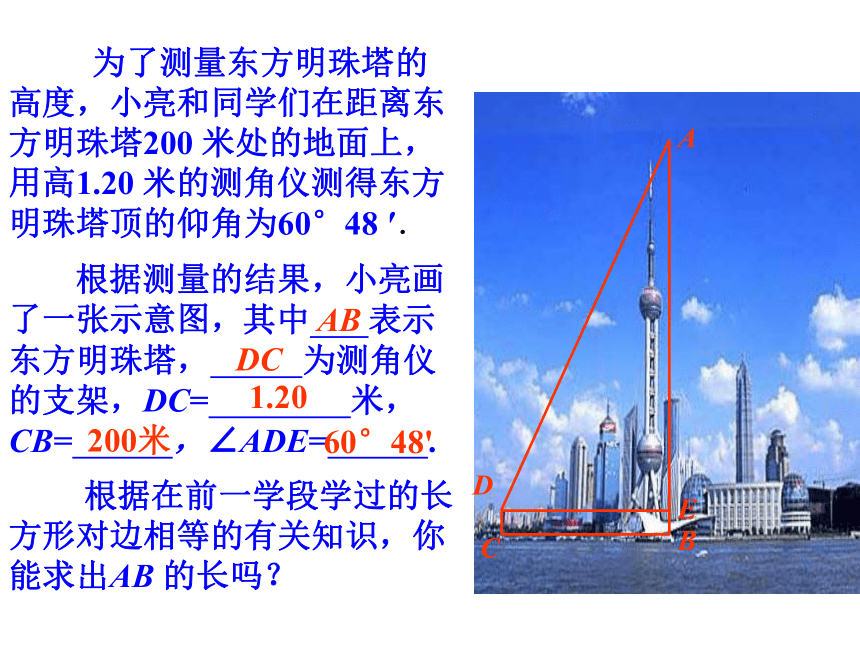
为了测量东方明珠塔的高度,小亮和同学们在距离东方明珠塔200 米处的地面上,用高1.20 米的测角仪测得东方明珠塔顶的仰角为60°48 ′. 其中 表示东方明珠塔, 为测角仪的支架,DC= 米,CB= ,∠ADE= . 根据测量的结果,小亮画了一张示意图,200米60°48'ABDC 根据在前一学段学过的长方形对边相等的有关知识,你能求出AB 的长吗?1.20解:根据长方形对边相等,EB=DC,DE=CB.在Rt△ABC中,∠AED=90°, ∠ADE= 60°48′.AE=DE·tan ∠ADE =200·tan60°48 ′≈357.86(米).所以AB=AE+EB≈ 357.86 +1.20=359.06 (米).答:东方明珠塔的高度约为359.06 米.
即中柱BC 长为2 . 44 米,上弦AB 长为5 . 56 米.例1 如图,厂房屋顶人字架的跨度为10 米,上弦AB=BD,∠A = 260 .求中柱BC 和上弦AB 的长(精确到0 . 01 米).解:由题意可知,△ ABD 是等腰三角形,BC是底边AD 上的高,AC = CD , AD = 10 米.在Rt △ABC 中∠ACB =90°, ∠A =26 °,例题讲解例2 如图,某直升飞机执行海上搜救任务,在空中A 处观测到海面上有一目标B ,俯角是α= 18°23 ' ,这时飞机的高度为1500 米,求飞机A与目标B的水平距离(精确到1 米). 在Rt△ABC中,AC=1500 米,∠ABC=∠α= 18°23 ' . 解:设经过B点的水平线为BC,作AC⊥BC,垂足为C .即飞机A与目标B的水平距离约为4 514 米.练习1 .如图,在电线杆上离地面6 米处用拉线固定电线杆,拉线和地面之间的夹角为60° , 求拉线AC 的长和拉线下端点A 与线杆底部D 的距离(精确到0 . 1 米). 2.如图,一架梯子斜靠在墙上,梯子顶端到地面的距离BC = 3.2 米,底端到墙根的距离
AC = 2.4 米. (1)求梯子的长度和梯子与地面所成角的大小(精确到1 ' ) ; (2) 如果把梯子的底端到墙角的距离减少0 . 4 米,那么梯子与地面所成的角是多少?AC≈5.2米AD=3.0米∠BAC≈53°8′AB=4.0米,∠BAC=60°2.会根据题意把实际问题转化为数学问题,然后利用解直角三角形的知识,明确已知量和未知量,选择合适的三角比,从而求得未知量.从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.1. 从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;课堂小结作业必做题:课本P83 A组 1、2、8题
选做题:课本P83 A组 3题同学们,
再见!
广角镜,用雷达测定目标的高度
雷达是利用电磁波探测目标的位置、速度和其他特征的电子设备.目标的距离可通过测定电磁波从雷达到目标的往返时间来确定.利用雷达天线的定向辐射特性,可测定目标的方位和仰角,根据目标距离和仰角可以计算出目标的高度.
假设大地是一个平面,如果目标的仰角为θ,根据电磁波的传播速度及其来回所用的时间,可以计算出雷达与目标之间的直线距离d (图9 一16 ) .这时目标的高度为h = dsin θ .然而,大地并非平面,而是曲面,因此计算目标高度的近似公式是
h 二d sin θ +
其中,R 表示地球的半径(约等于6370 千米)图9 一16
有几种情况?两个元素(至少一个是边)两条边或一边一角1.直角三角形的边角关系:温故知新 上海东方明珠塔于1994 年10 月1 日建成,在各国广播电视塔的排名榜中,当时其高度列亚洲第一、世界第三.与外滩的“万国建筑博览群”隔江相望.在塔顶俯瞰上海风景,美不胜收.运用本章所学过的知识,能测出东方明珠塔的高度来吗? 小 资 料在实际测量中的角从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角; 为了测量仰角和俯角,如果没有专门的仪器,可以自制一个简易测倾器.如图所示,简易测倾器由铅锤、度盘、支杆和螺检四部分组成,你能与同学合作制作一个简易测倾器吗?试一试.
为了测量东方明珠塔的高度,小亮和同学们在距离东方明珠塔200 米处的地面上,用高1.20 米的测角仪测得东方明珠塔顶的仰角为60°48 ′. 其中 表示东方明珠塔, 为测角仪的支架,DC= 米,CB= ,∠ADE= . 根据测量的结果,小亮画了一张示意图,200米60°48'ABDC 根据在前一学段学过的长方形对边相等的有关知识,你能求出AB 的长吗?1.20解:根据长方形对边相等,EB=DC,DE=CB.在Rt△ABC中,∠AED=90°, ∠ADE= 60°48′.AE=DE·tan ∠ADE =200·tan60°48 ′≈357.86(米).所以AB=AE+EB≈ 357.86 +1.20=359.06 (米).答:东方明珠塔的高度约为359.06 米.
即中柱BC 长为2 . 44 米,上弦AB 长为5 . 56 米.例1 如图,厂房屋顶人字架的跨度为10 米,上弦AB=BD,∠A = 260 .求中柱BC 和上弦AB 的长(精确到0 . 01 米).解:由题意可知,△ ABD 是等腰三角形,BC是底边AD 上的高,AC = CD , AD = 10 米.在Rt △ABC 中∠ACB =90°, ∠A =26 °,例题讲解例2 如图,某直升飞机执行海上搜救任务,在空中A 处观测到海面上有一目标B ,俯角是α= 18°23 ' ,这时飞机的高度为1500 米,求飞机A与目标B的水平距离(精确到1 米). 在Rt△ABC中,AC=1500 米,∠ABC=∠α= 18°23 ' . 解:设经过B点的水平线为BC,作AC⊥BC,垂足为C .即飞机A与目标B的水平距离约为4 514 米.练习1 .如图,在电线杆上离地面6 米处用拉线固定电线杆,拉线和地面之间的夹角为60° , 求拉线AC 的长和拉线下端点A 与线杆底部D 的距离(精确到0 . 1 米). 2.如图,一架梯子斜靠在墙上,梯子顶端到地面的距离BC = 3.2 米,底端到墙根的距离
AC = 2.4 米. (1)求梯子的长度和梯子与地面所成角的大小(精确到1 ' ) ; (2) 如果把梯子的底端到墙角的距离减少0 . 4 米,那么梯子与地面所成的角是多少?AC≈5.2米AD=3.0米∠BAC≈53°8′AB=4.0米,∠BAC=60°2.会根据题意把实际问题转化为数学问题,然后利用解直角三角形的知识,明确已知量和未知量,选择合适的三角比,从而求得未知量.从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.1. 从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;课堂小结作业必做题:课本P83 A组 1、2、8题
选做题:课本P83 A组 3题同学们,
再见!
广角镜,用雷达测定目标的高度
雷达是利用电磁波探测目标的位置、速度和其他特征的电子设备.目标的距离可通过测定电磁波从雷达到目标的往返时间来确定.利用雷达天线的定向辐射特性,可测定目标的方位和仰角,根据目标距离和仰角可以计算出目标的高度.
假设大地是一个平面,如果目标的仰角为θ,根据电磁波的传播速度及其来回所用的时间,可以计算出雷达与目标之间的直线距离d (图9 一16 ) .这时目标的高度为h = dsin θ .然而,大地并非平面,而是曲面,因此计算目标高度的近似公式是
h 二d sin θ +
其中,R 表示地球的半径(约等于6370 千米)图9 一16
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
