人教版九年级上册25.2 用列举法求概率课件(共24张PPT)
文档属性
| 名称 | 人教版九年级上册25.2 用列举法求概率课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 804.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 07:26:38 | ||
图片预览





文档简介
(共24张PPT)
25.2用列举法求概率(2)
本节课学习目标:
1.能够运用列表法和画树状图法计算简单随机试验中事件发生的概率;
2.能够根据题意和实际背景区分放回型(独立型)和不放回型(关联型)问题.
学习重点:
能够运用列举法(包括列表法和画树状图法)计算简单随机试验中事件发生的概率;
学习难点:
根据题意和实际背景区分放回型(独立型)和不放回型(关联型)问题.
复习回顾
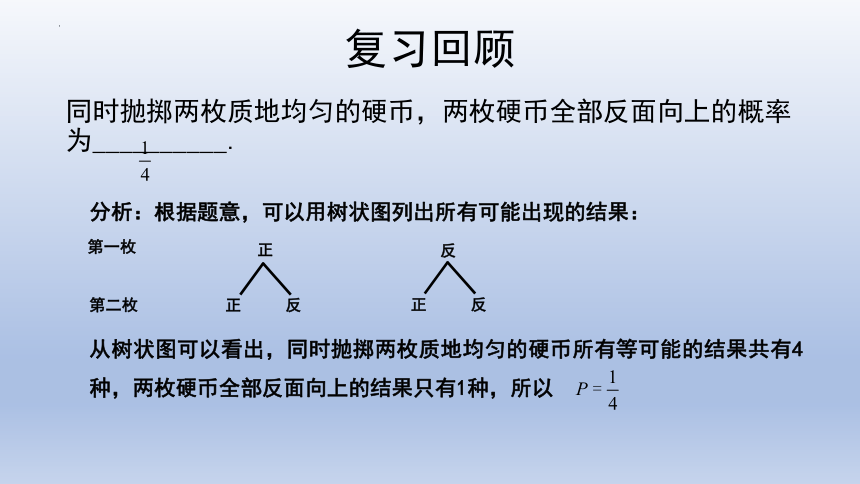
同时抛掷两枚质地均匀的硬币,两枚硬币全部反面向上的概率为__________.
分析:根据题意,可以用树状图列出所有可能出现的结果:
第一枚
第二枚
正
反
正
反
正
反
从树状图可以看出,同时抛掷两枚质地均匀的硬币所有等可能的结果共有4种,两枚硬币全部反面向上的结果只有1种,所以
例:在一个布袋中装有1个红球和2个蓝球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,放回搅匀再摸出第二个球,求两次都摸到蓝球的概率;
(2)搅匀后从中摸出一个球记下颜色,不放回继续再摸出第二个球,求两次都摸到蓝球的概率.
例题讲解
解:
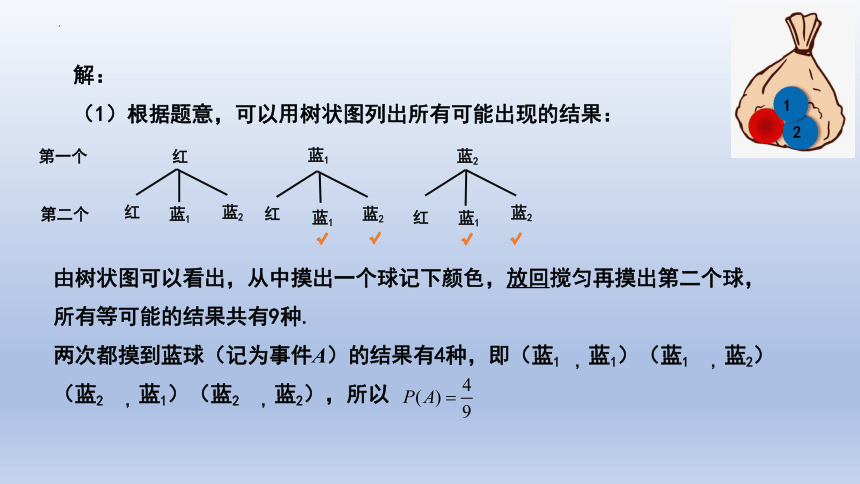
(1)根据题意,可以用树状图列出所有可能出现的结果:
由树状图可以看出,从中摸出一个球记下颜色,放回搅匀再摸出第二个球,所有等可能的结果共有9种.
两次都摸到蓝球(记为事件A)的结果有4种,即(蓝1 ,蓝1)(蓝1 ,蓝2)(蓝2 ,蓝1)(蓝2 ,蓝2),所以
1
2
蓝1
蓝2
红
第一个
红
蓝1
蓝2
第二个
红
蓝1
蓝2
红
蓝1
蓝2
√
√
√
√
思考
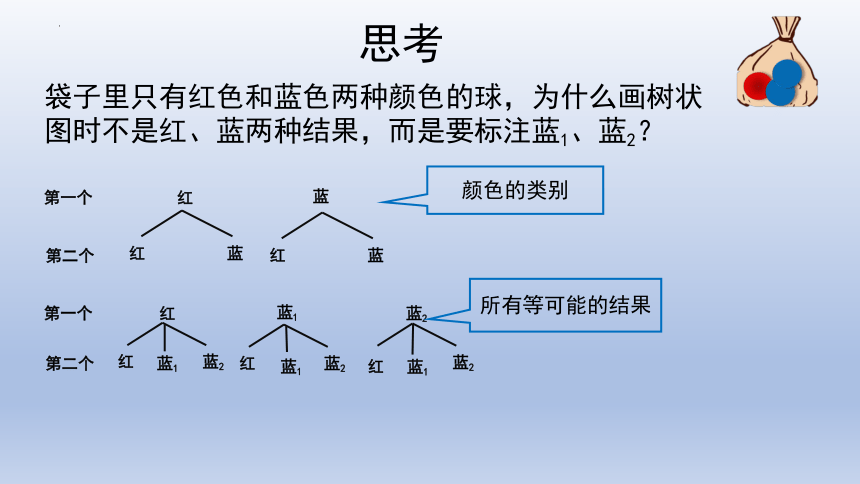
袋子里只有红色和蓝色两种颜色的球,为什么画树状图时不是红、蓝两种结果,而是要标注蓝1、蓝2?
蓝1
蓝2
红
第一个
红
蓝1
蓝2
第二个
红
蓝1
蓝2
红
蓝1
蓝2
蓝
红
第一个
红
蓝
第二个
红
蓝
所有等可能的结果
颜色的类别
例:在一个布袋中装有1个红球和2个蓝球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,放回搅匀再摸出第二个球,求两次都摸到蓝球的概率;
(2)搅匀后从中摸出一个球记下颜色,不放回继续再摸出第二个球,求两次都摸到蓝球的概率.
例题讲解
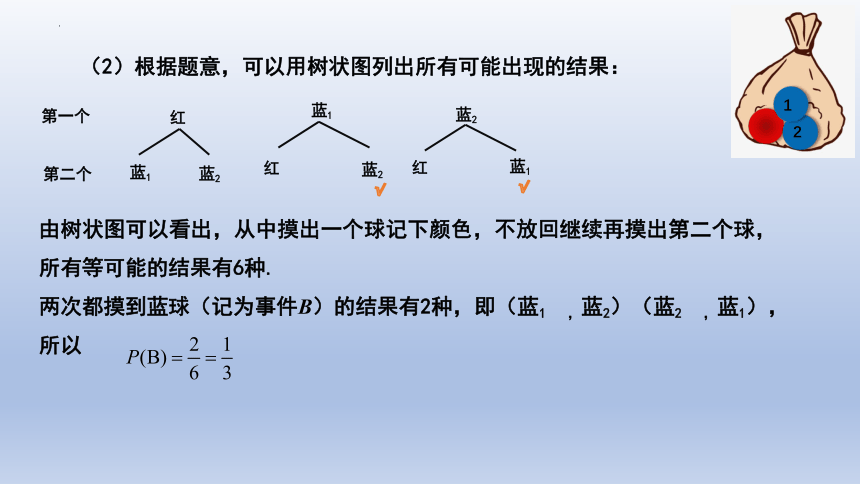
(2)根据题意,可以用树状图列出所有可能出现的结果:
由树状图可以看出,从中摸出一个球记下颜色,不放回继续再摸出第二个球,所有等可能的结果有6种.
两次都摸到蓝球(记为事件B)的结果有2种,即(蓝1 ,蓝2)(蓝2 ,蓝1),所以
1
2
蓝1
蓝2
红
第一个
蓝1
蓝2
第二个
√
√
红
蓝2
红
蓝1
归纳
放回
不放回
第二步不受第一步影响,
每一步之间相互独立
第二步受到第一步影响,
每一步之间相互关联
课堂练习
1.学校食堂今日供应的菜品包括:番茄炒蛋、芹菜炒肉片、凉瓜炒牛肉和南瓜蒸排骨.每人可以从中任意选取两样(不重复选菜).如果某同学选取这四种菜品的可能性大小相同,求他恰好选中番茄炒蛋和南瓜蒸排骨的概率.
解:若番茄炒蛋、芹菜炒肉片、凉瓜炒牛肉、南瓜蒸排骨分别记为A、B、C、D.
根据题意,可以用树状图列出所有可能出现的结果:
由上表可以看出,从四种菜品中选取两种,所有等可能的结果有12种.
恰好选中番茄炒蛋和南瓜蒸排骨(记为事件M)的结果有2种,即(A,D)(D,A),所以
C
D
A
B
第一个
B
C
D
第二个
√
√
A
C
D
A
B
D
A
B
C
2. 假定鸟卵孵化后,雏鸟为雌鸟与雄鸟的概率相同.如果3枚鸟卵全部成功孵化,那么3只雏鸟中恰有2只雄鸟的概率是多少?
解:根据题意,可以画出如下的树状图:
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
第一枚
第二枚
第三枚
由树状图可以看出,所有等可能的结果共有8种.
3只雏鸟中恰有2只雄鸟(记为事件A)的结果有3种,即(雌,雄,雄)(雄,雌,雄)(雄,雄,雌).所以
√
√
√
3. 在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1、2、3、4,乙口袋中的小球上分别标有数字2、3、4,先从甲口袋中任意摸出一个小球,记下数字为m,再从乙口袋中摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2)若m、n都是方程x2-5x+6=0的解时,则小明获胜;若m、n都不是方程x2-5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?
4
甲
乙
3
2
1
3
2
4
(1)解:根据题意,可以用下表列出所有可能出现的结果:
由上表可以看出,所有等可能的结果共有12种.
4
甲
乙
3
2
1
3
2
4
m
n
1
2
3
4
2
3
4
(1,2)
(1,3)
(1,4)
(2,2)
(2,3)
(2,4)
(3,2)
(3,3)
(3,4)
(4,2)
(4,3)
(4,4)
3. 在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1、2、3、4,乙口袋中的小球上分别标有数字2、3、4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2)若m、n都是方程x2-5x+6=0的解时,则小明获胜;若m、n都不是方程x2-5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?
4
甲
乙
3
2
1
3
2
4
m n 1 2 3 4
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
由上表可以看出,所有等可能的结果共有12种.
(2)解:方程x2-5x+6=0的解为x1=2,x2=3
m、n都不是方程x2-5x+6=0的解(记为事件B)的结果有2种,即(1,4)(4,4),所以
所以小明获胜的概率比小利大.
m、n都是方程x2-5x+6=0 的解(记为事件A)的结果有4种,即(2,2)(2,3)(3,2)(3,3)所以
课堂小结
计算简单随机事件发生的概率
疑问一
有些问题既可以用列表法,也可以用画树状图法,那这两种方法的优势和劣势分别是什么呢?在具体的题目中,应该如何选择合适的方法解决问题呢?
回答
1.如果试验是分两步完成的,那用列表法和画树状图法都可以解决问题。但是试验在三步或三步以上,那二维表格就难以表现,只能选择画树状图法了。
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
第一枚
第二枚
第三枚
如课堂练习2鸟卵孵化问题:
回答
2.有些具体问题,虽然是两步完成,但是选择列表法会比画树状图法更简洁.
m n 1 2 3 4
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
列表法
树状图法
由树状图可知,所有等可能的结果有12种,分别是(1,2)(1,3)(1,4) (2,2)(2,3)(2,4)
(3,2)(3,3)(3,4) (4,2)(4,3)(4,4).
1
第一个小球m
2
3
4
第二个小球n
2
2
3
4
3
2
3
4
4
2
3
4
如课堂练习3:题目要求“先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.并表示出所有(m,n)可能的结果”.
疑问二
在画树状图时,每一层的先后顺序会影响结果吗?
回答
1.若每步之间是关联型,第二步只能在第一步的基础上确定所有结果.
如例题第(2)题:“搅匀后从中摸出一个球记下颜色,不放回继续再摸出第二个球”.
蓝1
蓝2
红
第一个
蓝1
蓝2
第二个
红
蓝2
红
蓝1
回答
2.若每步之间是独立型,则先后顺序无影响.
树状图一
树状图二
红
甲布袋
红
蓝1
蓝2
乙布袋
绿
红
蓝1
蓝2
红
甲布袋
红
绿
乙布袋
蓝1
红
绿
蓝2
红
绿
由上面两个树状图可以看出,所有等可能的结果有6种,其中两个球恰好一个蓝色,一个绿色的结果有2种,分别是绿蓝1 、绿蓝2 ,所以
√
√
√
√
甲布袋里有一个红球,两个蓝球;乙布袋里有一个红球,一个绿球,它们除颜色外其他都相同.从每个袋子里各取出一个球,两个球恰好一个蓝色,一个绿色的概率是多少?
25.2用列举法求概率(2)
本节课学习目标:
1.能够运用列表法和画树状图法计算简单随机试验中事件发生的概率;
2.能够根据题意和实际背景区分放回型(独立型)和不放回型(关联型)问题.
学习重点:
能够运用列举法(包括列表法和画树状图法)计算简单随机试验中事件发生的概率;
学习难点:
根据题意和实际背景区分放回型(独立型)和不放回型(关联型)问题.
复习回顾
同时抛掷两枚质地均匀的硬币,两枚硬币全部反面向上的概率为__________.
分析:根据题意,可以用树状图列出所有可能出现的结果:
第一枚
第二枚
正
反
正
反
正
反
从树状图可以看出,同时抛掷两枚质地均匀的硬币所有等可能的结果共有4种,两枚硬币全部反面向上的结果只有1种,所以
例:在一个布袋中装有1个红球和2个蓝球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,放回搅匀再摸出第二个球,求两次都摸到蓝球的概率;
(2)搅匀后从中摸出一个球记下颜色,不放回继续再摸出第二个球,求两次都摸到蓝球的概率.
例题讲解
解:
(1)根据题意,可以用树状图列出所有可能出现的结果:
由树状图可以看出,从中摸出一个球记下颜色,放回搅匀再摸出第二个球,所有等可能的结果共有9种.
两次都摸到蓝球(记为事件A)的结果有4种,即(蓝1 ,蓝1)(蓝1 ,蓝2)(蓝2 ,蓝1)(蓝2 ,蓝2),所以
1
2
蓝1
蓝2
红
第一个
红
蓝1
蓝2
第二个
红
蓝1
蓝2
红
蓝1
蓝2
√
√
√
√
思考
袋子里只有红色和蓝色两种颜色的球,为什么画树状图时不是红、蓝两种结果,而是要标注蓝1、蓝2?
蓝1
蓝2
红
第一个
红
蓝1
蓝2
第二个
红
蓝1
蓝2
红
蓝1
蓝2
蓝
红
第一个
红
蓝
第二个
红
蓝
所有等可能的结果
颜色的类别
例:在一个布袋中装有1个红球和2个蓝球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,放回搅匀再摸出第二个球,求两次都摸到蓝球的概率;
(2)搅匀后从中摸出一个球记下颜色,不放回继续再摸出第二个球,求两次都摸到蓝球的概率.
例题讲解
(2)根据题意,可以用树状图列出所有可能出现的结果:
由树状图可以看出,从中摸出一个球记下颜色,不放回继续再摸出第二个球,所有等可能的结果有6种.
两次都摸到蓝球(记为事件B)的结果有2种,即(蓝1 ,蓝2)(蓝2 ,蓝1),所以
1
2
蓝1
蓝2
红
第一个
蓝1
蓝2
第二个
√
√
红
蓝2
红
蓝1
归纳
放回
不放回
第二步不受第一步影响,
每一步之间相互独立
第二步受到第一步影响,
每一步之间相互关联
课堂练习
1.学校食堂今日供应的菜品包括:番茄炒蛋、芹菜炒肉片、凉瓜炒牛肉和南瓜蒸排骨.每人可以从中任意选取两样(不重复选菜).如果某同学选取这四种菜品的可能性大小相同,求他恰好选中番茄炒蛋和南瓜蒸排骨的概率.
解:若番茄炒蛋、芹菜炒肉片、凉瓜炒牛肉、南瓜蒸排骨分别记为A、B、C、D.
根据题意,可以用树状图列出所有可能出现的结果:
由上表可以看出,从四种菜品中选取两种,所有等可能的结果有12种.
恰好选中番茄炒蛋和南瓜蒸排骨(记为事件M)的结果有2种,即(A,D)(D,A),所以
C
D
A
B
第一个
B
C
D
第二个
√
√
A
C
D
A
B
D
A
B
C
2. 假定鸟卵孵化后,雏鸟为雌鸟与雄鸟的概率相同.如果3枚鸟卵全部成功孵化,那么3只雏鸟中恰有2只雄鸟的概率是多少?
解:根据题意,可以画出如下的树状图:
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
第一枚
第二枚
第三枚
由树状图可以看出,所有等可能的结果共有8种.
3只雏鸟中恰有2只雄鸟(记为事件A)的结果有3种,即(雌,雄,雄)(雄,雌,雄)(雄,雄,雌).所以
√
√
√
3. 在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1、2、3、4,乙口袋中的小球上分别标有数字2、3、4,先从甲口袋中任意摸出一个小球,记下数字为m,再从乙口袋中摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2)若m、n都是方程x2-5x+6=0的解时,则小明获胜;若m、n都不是方程x2-5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?
4
甲
乙
3
2
1
3
2
4
(1)解:根据题意,可以用下表列出所有可能出现的结果:
由上表可以看出,所有等可能的结果共有12种.
4
甲
乙
3
2
1
3
2
4
m
n
1
2
3
4
2
3
4
(1,2)
(1,3)
(1,4)
(2,2)
(2,3)
(2,4)
(3,2)
(3,3)
(3,4)
(4,2)
(4,3)
(4,4)
3. 在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1、2、3、4,乙口袋中的小球上分别标有数字2、3、4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2)若m、n都是方程x2-5x+6=0的解时,则小明获胜;若m、n都不是方程x2-5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?
4
甲
乙
3
2
1
3
2
4
m n 1 2 3 4
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
由上表可以看出,所有等可能的结果共有12种.
(2)解:方程x2-5x+6=0的解为x1=2,x2=3
m、n都不是方程x2-5x+6=0的解(记为事件B)的结果有2种,即(1,4)(4,4),所以
所以小明获胜的概率比小利大.
m、n都是方程x2-5x+6=0 的解(记为事件A)的结果有4种,即(2,2)(2,3)(3,2)(3,3)所以
课堂小结
计算简单随机事件发生的概率
疑问一
有些问题既可以用列表法,也可以用画树状图法,那这两种方法的优势和劣势分别是什么呢?在具体的题目中,应该如何选择合适的方法解决问题呢?
回答
1.如果试验是分两步完成的,那用列表法和画树状图法都可以解决问题。但是试验在三步或三步以上,那二维表格就难以表现,只能选择画树状图法了。
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
雌鸟
雄鸟
第一枚
第二枚
第三枚
如课堂练习2鸟卵孵化问题:
回答
2.有些具体问题,虽然是两步完成,但是选择列表法会比画树状图法更简洁.
m n 1 2 3 4
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
列表法
树状图法
由树状图可知,所有等可能的结果有12种,分别是(1,2)(1,3)(1,4) (2,2)(2,3)(2,4)
(3,2)(3,3)(3,4) (4,2)(4,3)(4,4).
1
第一个小球m
2
3
4
第二个小球n
2
2
3
4
3
2
3
4
4
2
3
4
如课堂练习3:题目要求“先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.并表示出所有(m,n)可能的结果”.
疑问二
在画树状图时,每一层的先后顺序会影响结果吗?
回答
1.若每步之间是关联型,第二步只能在第一步的基础上确定所有结果.
如例题第(2)题:“搅匀后从中摸出一个球记下颜色,不放回继续再摸出第二个球”.
蓝1
蓝2
红
第一个
蓝1
蓝2
第二个
红
蓝2
红
蓝1
回答
2.若每步之间是独立型,则先后顺序无影响.
树状图一
树状图二
红
甲布袋
红
蓝1
蓝2
乙布袋
绿
红
蓝1
蓝2
红
甲布袋
红
绿
乙布袋
蓝1
红
绿
蓝2
红
绿
由上面两个树状图可以看出,所有等可能的结果有6种,其中两个球恰好一个蓝色,一个绿色的结果有2种,分别是绿蓝1 、绿蓝2 ,所以
√
√
√
√
甲布袋里有一个红球,两个蓝球;乙布袋里有一个红球,一个绿球,它们除颜色外其他都相同.从每个袋子里各取出一个球,两个球恰好一个蓝色,一个绿色的概率是多少?
同课章节目录
