人教版八年级下册19.3 课题学习 选择方案课件(共27张PPT)
文档属性
| 名称 | 人教版八年级下册19.3 课题学习 选择方案课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 598.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 07:28:52 | ||
图片预览








文档简介
(共27张PPT)
第十九章一次函数复习课
从实际问题说起
例1.小王骑自行车从A地到B地办事情,半小时后,小张开汽车沿着同一条路从A地赶往B地.小王的速度是10km/h,小张的速度为60km/h.
(1)用语言描述小王和小张在路上前后位置的变化;
(2)试判断什么时间段小王在前?什么时间段小张在前?并说明理由.
从实际问题说起
小王骑自行车从A地到B地办事情,半小时后,小张开汽车沿着同一条路从A 地赶往B地.小王的速度是10km/h,小张的速度为60km/h.
(1)用语言描述小王和小张在路上前后位置的变化;
解:(1)小王先出发0.5 h,因此开始时小王在前,小张在后;由于小张的速度比小王快,因此,后来小张追上小王,追上以后,小张一直在前.
小王骑自行车从A地到B地办事情,半小时后,小张开汽车沿着同一条路从A地赶往B地.小王的速度是10km/h,小张的速度为60km/h.
(2)试判断什么时间段小王在前?什么时间段小张在前?并说明理由.
从实际问题说起
解:(2)路程、速度、时间:
路程=速度时间
速度= 时间=
假设小王出发后行驶的时间为x小时,小王、小张离A地的路程分别为、,则
小王离A地的路程与之间的关系式为:
小张离A地的路程与之间的关系式为:.
时,,解得
当时,小王在前;当,小张在前.
小王骑自行车从A地到B地办事情,半小时后,小张开汽车沿着同一条路从A地赶往B地.小王的速度是10km/h,小张的速度为60km/h.
(2)试判断什么时间段小王在前?什么时间段小张在前?并说明理由.
从实际问题说起
解:在同一平面直角坐标系中画出两个函数图象:
8
6
4
2
2
1
O
x
y
=10x
=60x-30
(小王)
(小张)
0.6
知识回顾
(1)用你自己的语言来描述一下什么是函数?怎样确定函数的自变量取值范围?
(2)函数有哪几种表示方法?它们各有什么特点?
(3)例1中出现的函数是什么函数,它们的解析式是什么样的形式?图象有哪些性质?
(4)例1中小王、小张离A地的路程与时间之间的关系都可以用一次函数的关系式来表示,通过第(2)问的解决,你能够理解一次函数和方程(组)、不等式之间的关系吗?
知识点一:函数的概念
1. 常量与变量(例1中哪些量是变量?哪些量是常量?)
叫变量, 叫常量.
数值发生变化的量
数值始终不变的量
知识梳理
练习1:某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A.数100和η,t都是变量
B.数100和η都是常量
C.η和t是变量
D.数100和t都是常
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
2.函数定义:
知识点一:函数的概念
知识梳理
练习2:如图,表示y是x的函数图象的是( )
知识点一:函数的概念
知识梳理
3.自变量的取值范围
D
知识点一:函数的概念
知识梳理
4.函数的图象:
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
解析式法
图象法
6.函数的三种表示方法:
5.描点法画图象的步骤:
列表、描点、连线
1.正比例函数的概念:
形如 的函数叫做正比例函数.
知识点二:正比例函数
知识梳理
练习2.下列哪些式子的正比例函数?
正比例函数:(1)(3)
A
知识点二:正比例函数
知识梳理
2.正比例函数的图象与性质
图像:正比例函数的图像是一条过原点的直线
性质:当k>0时,正比例函数图象经过一、三象限,y随着x的增大而增大
当k<0时,正比例函数图象经过二、四象限,y随着x的增大而减小
B
A
知识梳理
知识点三:一次函数
1.一次函数的概念:
形如 的函数叫做一次函数.
① ④ ⑤
知识梳理
知识点三:一次函数
2.一次函数图象与性质:一次函数的图象是一条直线;画一次函数图象只要确定两个点即可.
函数 字母系数取值 ( k>0 ) 图象 经过的象限 函数性质
y=kx+b (k≠0) b>0 y随x
增大而
增大
b=0
b<0
第一、三象限
第一、二、三象限
第一、三、四象限
关注与坐标轴的交点!(0,b)0)
知识梳理
知识点三:一次函数
函数 字母系数取值 ( k<0 ) 图象 经过的象限 函数性质
y=kx+b (k≠0) b>0 y随x
增大而
减小
b=0
b<0
第一、二、四象限
第二、四象限
第二、三、四象限
2.一次函数图象与性质:一次函数的图象是一条直线;画一次函数图象只要确定两个点即可
知识梳理
知识点三:一次函数
B
知识梳理
知识点三:一次函数
3.待定系数法求一次函数
练习5.直线 经过点(-2,2),则该直线的解析式是______________.
练习6.若直线 与直线 平行,且与y轴交点的纵坐标为-2.则该直线
的解析式为_______________.
知识梳理
知识点三:一次函数
3.待定系数法求一次函数
求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.这种求解析式的方法叫待定系数法.
知识梳理
知识点四:一次函数与方程(组)、不等式
1.一次函数与一元一次方程
求一元一次方程 kx+b=0(k≠0)的解
求直线y=kx+b与x轴交点的横坐标。
从“函数图象”看
求一次函数y=kx+b
中y=0时x的值。
从“函数值”看
练习1.如图,方程 的解是 .
知识梳理
知识点四:一次函数与方程(组)、不等式
2.一次函数与一元一次不等式
求kx+b>0(或<0)(k≠0)的解集
求一次函数y=kx+b的值大于(或小于)0时,
自变量x的取值范围
从“函数值”看
从“函数图象”看
确定直线y=kx+b
在x轴上方(或下方)时对应x轴的哪一部分
练习2.如图,直线 交坐标轴于A,B两点,
则不等式 的解集是_________
知识梳理
知识点四:一次函数与方程(组)、不等式
3.一次函数与二元一次方程组
一般地,任何一个二元一次方程都可以化为一次函数 (k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
练习3.如图,利用函数图象解方程组 ,
则其解是
(4)∵该函数图象过点(1,4),代入得: ,解得 ,
∴该函数的解析式为 .
(3)∵y随着x的增大而减小,∴ ,解得 .
(2)∵函数的图象平行于直线 ,∴ ,解得 .
解:(1)∵函数是正比例函数,∴ ,且 ,解得 .
典例讲解
例2.已知函数 ;
(1)若该函数是正比例函数,求m的值;
(2)若函数的图象平行直线 ,求m的值;
(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(4)若这个函数图象过点(1,4),求这个函数的解析式.
【点睛】一次函数的图象与y轴交点的纵坐标就是y=kx+b中b的值;两条直线平行,其函数解析式中的自变量系数k相等;当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
典例讲解
例3.已知一次函数 的图象不经过第三象限,求m的取值范围.
【分析】图象不经过第三象限,则分两种情况:
1.只经过二、四象限;
2.经过一、二、四象限.所以需要进行分类讨论.
当一次函数经过一、二、四象限时:,解得:m<-1
综上可得:m-1.
.
解:当一次函数只经过二、四象限时:,解得:m=-1
.
拓展应用
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
例4.为美化广州市景,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在花城大道一侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
拓展应用
解(1)设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,依题意,得:
∴31≤x≤33.∵x 是整数,x 可取 31,32,33,∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
例4.为美化广州市景,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在花城大道一侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
拓展应用
方案①需成本:31×800+19×960=43040(元);
方案②需成本:32×800+18×960=42880(元);
方案③需成本:33×800+17×960=42720(元).
(2)方法一:
方法二:成本为:
y=800x+960(50-x)=-160x+48000(31≤x≤33).
根据一次函数的性质,y随x的增大而减小,
故当x=33时,y取得最小值为:
33×800+17×960=42720(元).
即最低成本是 42720 元.
【点睛】用一次函数解决实际问题,先理解清楚题意,把文字语言转化为数学语言,列出相应的关系式(不等式、方程),若是方案选择问题,则要求出自变量在取不同值时所对应的函数值,判断其大小关系,结合实际需求,选择最佳方案.
课堂小结
某些运动变化
的现实问题
函数
建立函
数模型
定义
自变量取值范围
表示法
一次函数
y=kx+b(k≠0)
应用
图象:一条直线
性质:
k>0,y 随x 的增大而增大
k<0,y 随x 的增大而减小
数形结合
一次函数与方程(组)、
不等式之间的关系
第十九章一次函数复习课
从实际问题说起
例1.小王骑自行车从A地到B地办事情,半小时后,小张开汽车沿着同一条路从A地赶往B地.小王的速度是10km/h,小张的速度为60km/h.
(1)用语言描述小王和小张在路上前后位置的变化;
(2)试判断什么时间段小王在前?什么时间段小张在前?并说明理由.
从实际问题说起
小王骑自行车从A地到B地办事情,半小时后,小张开汽车沿着同一条路从A 地赶往B地.小王的速度是10km/h,小张的速度为60km/h.
(1)用语言描述小王和小张在路上前后位置的变化;
解:(1)小王先出发0.5 h,因此开始时小王在前,小张在后;由于小张的速度比小王快,因此,后来小张追上小王,追上以后,小张一直在前.
小王骑自行车从A地到B地办事情,半小时后,小张开汽车沿着同一条路从A地赶往B地.小王的速度是10km/h,小张的速度为60km/h.
(2)试判断什么时间段小王在前?什么时间段小张在前?并说明理由.
从实际问题说起
解:(2)路程、速度、时间:
路程=速度时间
速度= 时间=
假设小王出发后行驶的时间为x小时,小王、小张离A地的路程分别为、,则
小王离A地的路程与之间的关系式为:
小张离A地的路程与之间的关系式为:.
时,,解得
当时,小王在前;当,小张在前.
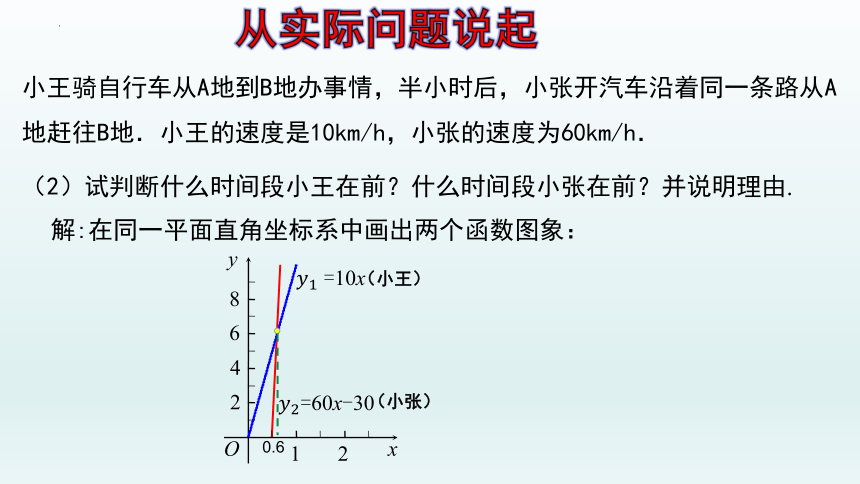
小王骑自行车从A地到B地办事情,半小时后,小张开汽车沿着同一条路从A地赶往B地.小王的速度是10km/h,小张的速度为60km/h.
(2)试判断什么时间段小王在前?什么时间段小张在前?并说明理由.
从实际问题说起
解:在同一平面直角坐标系中画出两个函数图象:
8
6
4
2
2
1
O
x
y
=10x
=60x-30
(小王)
(小张)
0.6
知识回顾
(1)用你自己的语言来描述一下什么是函数?怎样确定函数的自变量取值范围?
(2)函数有哪几种表示方法?它们各有什么特点?
(3)例1中出现的函数是什么函数,它们的解析式是什么样的形式?图象有哪些性质?
(4)例1中小王、小张离A地的路程与时间之间的关系都可以用一次函数的关系式来表示,通过第(2)问的解决,你能够理解一次函数和方程(组)、不等式之间的关系吗?
知识点一:函数的概念
1. 常量与变量(例1中哪些量是变量?哪些量是常量?)
叫变量, 叫常量.
数值发生变化的量
数值始终不变的量
知识梳理
练习1:某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A.数100和η,t都是变量
B.数100和η都是常量
C.η和t是变量
D.数100和t都是常
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
2.函数定义:
知识点一:函数的概念
知识梳理
练习2:如图,表示y是x的函数图象的是( )
知识点一:函数的概念
知识梳理
3.自变量的取值范围
D
知识点一:函数的概念
知识梳理
4.函数的图象:
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
解析式法
图象法
6.函数的三种表示方法:
5.描点法画图象的步骤:
列表、描点、连线
1.正比例函数的概念:
形如 的函数叫做正比例函数.
知识点二:正比例函数
知识梳理
练习2.下列哪些式子的正比例函数?
正比例函数:(1)(3)
A
知识点二:正比例函数
知识梳理
2.正比例函数的图象与性质
图像:正比例函数的图像是一条过原点的直线
性质:当k>0时,正比例函数图象经过一、三象限,y随着x的增大而增大
当k<0时,正比例函数图象经过二、四象限,y随着x的增大而减小
B
A
知识梳理
知识点三:一次函数
1.一次函数的概念:
形如 的函数叫做一次函数.
① ④ ⑤
知识梳理
知识点三:一次函数
2.一次函数图象与性质:一次函数的图象是一条直线;画一次函数图象只要确定两个点即可.
函数 字母系数取值 ( k>0 ) 图象 经过的象限 函数性质
y=kx+b (k≠0) b>0 y随x
增大而
增大
b=0
b<0
第一、三象限
第一、二、三象限
第一、三、四象限
关注与坐标轴的交点!(0,b)0)
知识梳理
知识点三:一次函数
函数 字母系数取值 ( k<0 ) 图象 经过的象限 函数性质
y=kx+b (k≠0) b>0 y随x
增大而
减小
b=0
b<0
第一、二、四象限
第二、四象限
第二、三、四象限
2.一次函数图象与性质:一次函数的图象是一条直线;画一次函数图象只要确定两个点即可
知识梳理
知识点三:一次函数
B
知识梳理
知识点三:一次函数
3.待定系数法求一次函数
练习5.直线 经过点(-2,2),则该直线的解析式是______________.
练习6.若直线 与直线 平行,且与y轴交点的纵坐标为-2.则该直线
的解析式为_______________.
知识梳理
知识点三:一次函数
3.待定系数法求一次函数
求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.这种求解析式的方法叫待定系数法.
知识梳理
知识点四:一次函数与方程(组)、不等式
1.一次函数与一元一次方程
求一元一次方程 kx+b=0(k≠0)的解
求直线y=kx+b与x轴交点的横坐标。
从“函数图象”看
求一次函数y=kx+b
中y=0时x的值。
从“函数值”看
练习1.如图,方程 的解是 .
知识梳理
知识点四:一次函数与方程(组)、不等式
2.一次函数与一元一次不等式
求kx+b>0(或<0)(k≠0)的解集
求一次函数y=kx+b的值大于(或小于)0时,
自变量x的取值范围
从“函数值”看
从“函数图象”看
确定直线y=kx+b
在x轴上方(或下方)时对应x轴的哪一部分
练习2.如图,直线 交坐标轴于A,B两点,
则不等式 的解集是_________
知识梳理
知识点四:一次函数与方程(组)、不等式
3.一次函数与二元一次方程组
一般地,任何一个二元一次方程都可以化为一次函数 (k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
练习3.如图,利用函数图象解方程组 ,
则其解是
(4)∵该函数图象过点(1,4),代入得: ,解得 ,
∴该函数的解析式为 .
(3)∵y随着x的增大而减小,∴ ,解得 .
(2)∵函数的图象平行于直线 ,∴ ,解得 .
解:(1)∵函数是正比例函数,∴ ,且 ,解得 .
典例讲解
例2.已知函数 ;
(1)若该函数是正比例函数,求m的值;
(2)若函数的图象平行直线 ,求m的值;
(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(4)若这个函数图象过点(1,4),求这个函数的解析式.
【点睛】一次函数的图象与y轴交点的纵坐标就是y=kx+b中b的值;两条直线平行,其函数解析式中的自变量系数k相等;当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
典例讲解
例3.已知一次函数 的图象不经过第三象限,求m的取值范围.
【分析】图象不经过第三象限,则分两种情况:
1.只经过二、四象限;
2.经过一、二、四象限.所以需要进行分类讨论.
当一次函数经过一、二、四象限时:,解得:m<-1
综上可得:m-1.
.
解:当一次函数只经过二、四象限时:,解得:m=-1
.
拓展应用
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
例4.为美化广州市景,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在花城大道一侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
拓展应用
解(1)设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,依题意,得:
∴31≤x≤33.∵x 是整数,x 可取 31,32,33,∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
例4.为美化广州市景,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在花城大道一侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
拓展应用
方案①需成本:31×800+19×960=43040(元);
方案②需成本:32×800+18×960=42880(元);
方案③需成本:33×800+17×960=42720(元).
(2)方法一:
方法二:成本为:
y=800x+960(50-x)=-160x+48000(31≤x≤33).
根据一次函数的性质,y随x的增大而减小,
故当x=33时,y取得最小值为:
33×800+17×960=42720(元).
即最低成本是 42720 元.
【点睛】用一次函数解决实际问题,先理解清楚题意,把文字语言转化为数学语言,列出相应的关系式(不等式、方程),若是方案选择问题,则要求出自变量在取不同值时所对应的函数值,判断其大小关系,结合实际需求,选择最佳方案.
课堂小结
某些运动变化
的现实问题
函数
建立函
数模型
定义
自变量取值范围
表示法
一次函数
y=kx+b(k≠0)
应用
图象:一条直线
性质:
k>0,y 随x 的增大而增大
k<0,y 随x 的增大而减小
数形结合
一次函数与方程(组)、
不等式之间的关系
