2022年北京市海淀区中考数学二模试卷讲评 课件(共113张PPT)
文档属性
| 名称 | 2022年北京市海淀区中考数学二模试卷讲评 课件(共113张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 36.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 06:57:43 | ||
图片预览








文档简介
(共113张PPT)
数学学科 评分细则及讲评建议
海淀区九年级第二学期期末练习
2022/5/25
1
一、命题立意
·以学定考,教、学、考一致
·以课标为纲,教材为抓手
·学考冲刺阶段的查缺补漏
2022/5/25
2
命题立意
严格依据课程标准命题。各地要认真落实依据义务教育课程标准命题的规定要求,坚决取消初中学业水平考试大纲或考试说明,不得超标命题和随意扩大、压减考试内容范围,严禁将高中课程内容、学科竞赛试题以及校外培训内容作为考试内容,确保依标命题、教考衔接。
科学设置试卷难度。各地要按照“两考合一”“兼顾毕业和升学”的功能定位,进一步对各相关学科中考试卷考试时长、容量、难度等提出规范要求,科学合理设置试卷难度,既要防止试卷过难增加学生学业负担,也要避免试卷过易难以体现区分度。要根据不同学科特点,合理设置试卷试题结构,减少记忆性试题,增加探究性、开放性、综合性试题,坚决防止偏题怪题,促进有效考查学生综合素质。
——教育部办公厅关于做好2022年中考命题工作的通知
2022/5/25
3
2022/5/25
4
命题立意
命题依据
以课标为纲
以教材为抓手
调研指向
命题原则
高频考点
回归课本
查缺补漏
诊断激励
素养立意,育人导向
核心素养
数学本质
通性通法
四基
四能
命题背景
双减
两考合一
疫情居家
2022/5/25
5
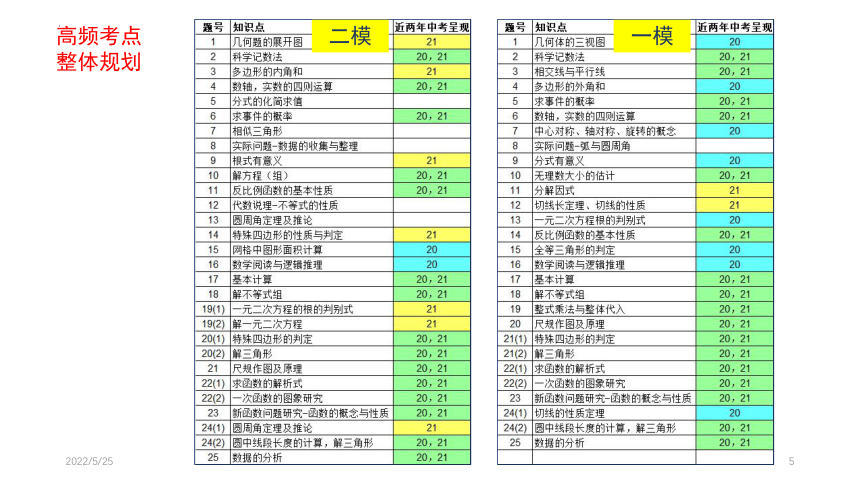
高频考点
整体规划
二模
一模
2022/5/25
6
对课本例题的简单改编
2022/5/25
7
从课本习题衍生,提炼数学思维
2022/5/25
8
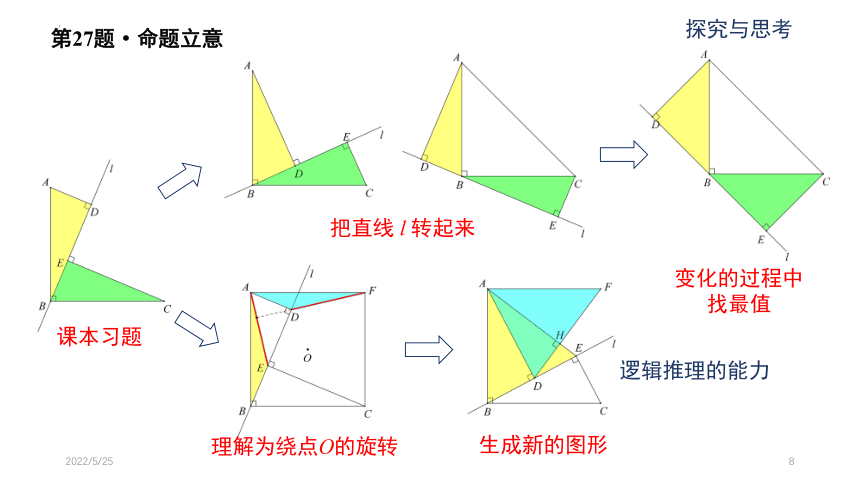
第27题·命题立意
课本习题
把直线 l 转起来
变化的过程中
找最值
理解为绕点O的旋转
生成新的图形
逻辑推理的能力
探究与思考
二、评分细则与讲评建议
·基本原则:给分有理,扣分有据,严格遵循评标
·总体上既要让更多的学生有获得感,又体现适当的区分度
·在冲刺阶段,适当关注学生的作答规范
·关于建系、共圆等课本以外的知识,用对不扣分,用错不找
等价采分点,从用的那一步开始不记分.
2022/5/25
9
2022/5/25
10
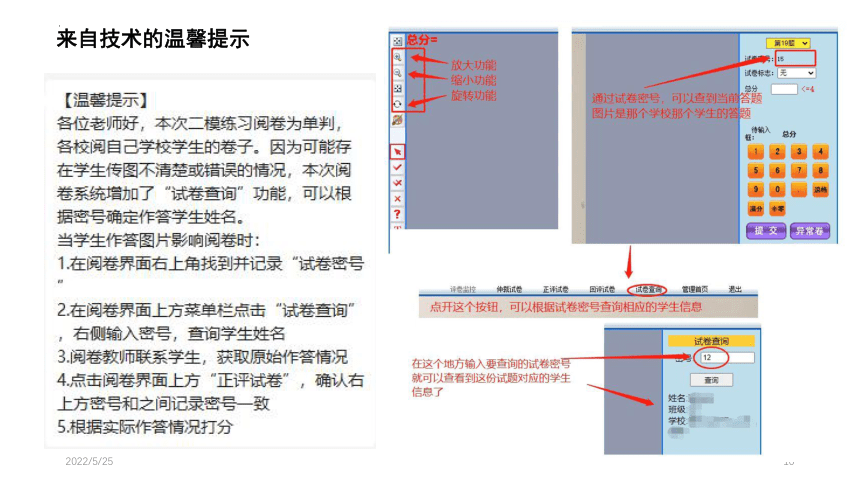
来自技术的温馨提示
第 1-8 题
2022/5/25
11
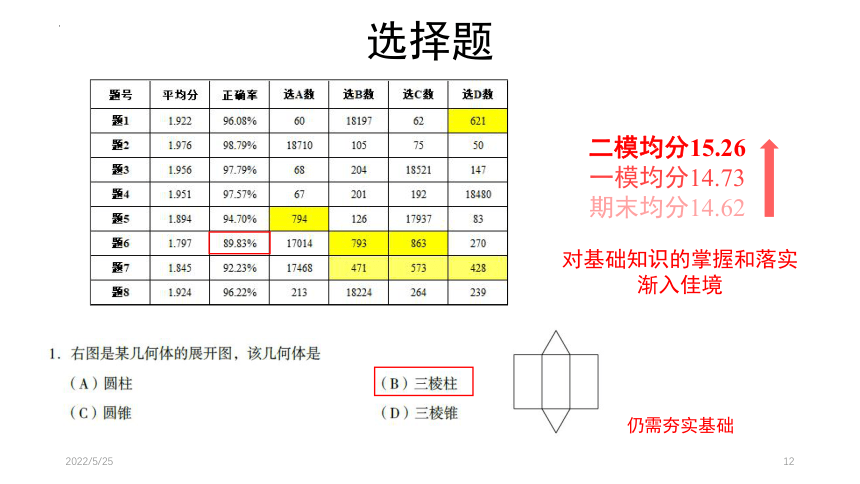
选择题
2022/5/25
12
二模均分15.26
一模均分14.73
期末均分14.62
仍需夯实基础
对基础知识的掌握和落实
渐入佳境
2022/5/25
13
4.2%错选B
4.6%错选C
2021
2020
2022/5/25
14
数据的收集、整理与分析
数学与生活的紧密联系
第 9-16 题
2022/5/25
15
2022/5/25
16
9-16题评分原则:
1、除16题每空1分,其他题目只有0分和2分,每道题均为完全正确才可得2分.
2、所有结果只要正确,没化简不扣分.
3、第10题没有大括号也可以,但必须写出x,y对应来,单独写1,3不给分!
写成y1>y2满分.
4、第12题只要非正数即可.
5、第13题可以不写单位“°”
第9-16题·评分细则
2022/5/25
17
9-16题评分原则:
6、第14题注意只能加一个条件:例如AC⊥EF,AF=AE, AE=EC.
典型错误:AF=EC,AE=FC,AF=FC=CE=EA(这是几个条件)
写成理由的不给分.
注意区别:AC是FE的垂直平分线×,FE是AC的垂直平分线√
7、第16题② 不考虑顺序.
第9-16题·评分细则
2022/5/25
18
第16题·讲评建议
1、怎样提取有效信息?
2、“最少”怎样体现?
2020
总和30
最大值10(有两个)
第 17 题
2022/5/25
19
2022/5/25
20
17题评分原则:
1、共5分,四个计算各1分,结果1分;
2、若只写答案,只给答案1分;(以下同,仅答案对无合理过程只给答案分)
3、若学生抄了题,抄错且完全做对,可以给4分,抄题且做错,按4分上限,
依据上述规则扣分,没抄题的按原题判。
第17题·评分细则
2022/5/25
21
第17题·评卷样例
5分
4分
藏得挺深
2022/5/25
第17题·评卷样例
3分
2分
0分,全都不对也少见
第 18 题
2022/5/25
23
2022/5/25
24
18题评分原则:
1、共5分,每个不等式解对得2分,最后解集对1分;
2、若单个不等式解错,但去括号、去分母等步骤有对的,给相应的步骤分1分;
3、最后解集写成区间形式不扣分.
4、抄了题的学生,抄错题且完全做对的,给4分,但抄错题还做错,按4分上限根据上述规则扣分, 没抄题的按原题判。
第18题·评分细则
2022/5/25
第18题·评卷样例
4分
4分
0分,全都不对也少见
4分
4分 抄错题了
2022/5/25
第18题·评卷样例
3分,去分母对了
0分,没图
因为是自己上传
报问题卷也没用..
第 19 题
2022/5/25
27
2022/5/25
28
19题评分原则:
1、共6分,第(1)问3分,① 依题意△>0 或 判别式列对1分,
② 化对1分,③ 解对1分.
2、第(2)问3分,① 确定m=0,② 写出方程,或者列出求根公式
③ 解正确各1分.
第19题·评分细则
看错条件,△也没对,0分
第19题·评卷样例
列对、化对2分,m为0对,方程对2分,共4分
1’
1’
1’
1’
第19题·评卷样例
(1)列对1分(注意列对和△>0算一个点!),
(2)m=0对,方程对2分,共计3分
不规范,不扣分,讲评注意强调
1’
1’
1’
第19题·评卷样例
列错,△>0也没写出来,0分
第19题·评卷样例
第(1)问0分,第(2)问仅m=0给1分
1’
第19题·评卷样例
3’
1’
1’
第(2)问没有写出方程和求根公式之一,扣1分,3分+2分
第19题·评卷样例
第(2)问,m对,方程对,配方法解方程错,扣1分,3+2
3’
1’
1’
第19题·评卷样例
3’
1’
1’
没拍全,但可以基本合理推断他写对了,可以给满分
第19题·评卷样例
第 20 题
2022/5/25
37
2022/5/25
38
20题(1)评分原则:
1、证明共3分,有两种方法,①中位线→②平行四边形→③矩形
①中位线→②三个直角→③矩形
这两种证明方法每一步1分.
2、如果没有证明平行四边形,由两个平行+直角得矩形,扣1分(上次说的暂不
扣,这次要执行!),三个直角如果没有出全,酌情扣分.
第20题·评分细则
2022/5/25
39
20题(2)评分原则:
1、共3分,AC、AE、BE三条线段各1分;
第20题·评分细则
学生方法1:
平行四边形+90°→矩形
第20题·评卷样例
学生方法2:三个90°→矩形
第20题·评卷样例
利用两组对边相等证平行四边形时,但有跳步
利用三个90°证平行四边形,最后三个角没有写连等没问题
老师易判错的地方
没有出平行四边形就得矩形扣1分
跳步严重
很不规范
第20题·评卷样例
实在是太聒噪
第20题·评卷样例
第20题·评卷样例
不忍直视
第 21 题
2022/5/25
46
2022/5/25
47
21题(1)(2)评分原则:
1、(1)无争议,
2、(2)角平分线位置对且字母标记正确1分,作图痕迹1分;画错角分线不给分!
注意如果选a且∠BAE的平分线画对也给分,画成直线或者线段不扣分.
第21题·评分细则
2022/5/25
48
21题(3)评分原则:
1、写理由1分:整体意思对即可给分,笔误不扣分,但圆周角、圆心角、弧、
一半等关键词不承认笔误;
2、填角1分,无争议.
第21题·评分细则
2022/5/25
49
第21题·评卷样例
作角平分线
作中垂线由三线合一得角平分线
2022/5/25
50
第21题·评卷样例
直线、线段不扣分
没有尺规作图痕迹
扣1分
P点位置标错扣1分
特殊情况:
若第1问选a,第2问根据a的描述,正确尺规作出了∠BAE的平分线及点P
第1问,0分
第2问,2分
第21题·评卷样例
依据:0分示例
关键词不承认笔误,不给分,弧,圆周角,圆心角,一半
第21题·评卷样例
第 22 题
2022/5/25
53
2022/5/25
54
22题评分原则:
1、(1) 共3分,交点纵坐标、m、反比例函数解析式各占1分;总体来说解析式
对且y = 6对即可满分.
2、(2) 共2分,完全正确2分,仅得到k>2或者k=2得1分,其余0分.
注意:这里把 k ≥ 2 分成两个点来考虑,回答k ≤ 2的也算他踩到了k=2
第22题·评分细则
第 23 题
2022/5/25
55
2022/5/25
56
23题评分原则:
1、(1)画图 共2分,描出所有点1分,用平滑曲线连接1分
要连上每个点,平滑的曲线,不出头.(连直线不给分,出头扣1分)
2、(2)①②各1分,①无争议,② 允许的范围:95-105(含边界,取小数不扣分).
3、(3) 1分,无争议
第23题·评分细则
95-105含边界
第(1)问 画图 2分
① 描点正确1分;
② 连线正确1分.
2分 忽略连线的毛边
2分 点贴着线即可
2分 忽略空心实心点
第23题·评卷样例
2分 平滑曲线
趋势正确
第23题·评卷样例
1分 描点正确
连线不完整,出头
1分 描点正确
两端均出头
1分 描点正确
一端出头
1分 描点正确
连线不完整
第23题·评卷样例
0分 描点有错误
第23题·评卷样例
2022/5/25
61
函数探究问题
2015、16、20 给定解析式
2017、18、19 几何为背景
落脚点
·函数的概念
·函数的基本性质
·函数的应用(结合实际)
西城
2022/5/25
62
昌平二模
丰台
第 24 题
2022/5/25
63
第24题·评分细则
第24题 满分 采分点及注意事项
第(1)小问 2分 圆周角 or 等边对等角 1分,
平行线证明正确 1分
第(2)小问 4分 答案正确 两个答案各1分,共2分
证明任何一个30°、60°角或者证出等边三角形 1分
计算出AG(CG)、CD(AF)或者是其他等效线段长,1分
2022/5/25
64
注:本题的关键在于是否能够正确推出特殊角,
所以需要看过程,凡推理不合理的均应扣分.
凡因书写不规范导致难以理解的过程均酌情扣分.
第一问 2分满
第24题·评卷样例
第24题·评卷样例
第二问 4分满
标答+
第24题·评卷样例
第24题·评卷样例
第24题·评卷样例
第24题·评卷样例
求AC长时证全等
第24题·评卷样例
2分
证明平行四边形
2分
第24题·评卷样例
0分
第24题·评卷样例
1分
第24题·评卷样例
2分
4分
第24题·评卷样例
△CAE≌△DOE
第24题·评卷样例
第24题·评卷样例
2分
1分
第24题·评卷样例
第24题·评卷样例
第24题·评卷样例
第 25 题
2022/5/25
81
第25题·评分细则
五个点5分,
前四个点没有争议,理由必须表述严谨方可得分
2022/5/25
82
第 26 题
2022/5/25
83
第26题·评分细则
第26题 满分 采分点及注意事项
第(1)小问 1分 只写 a 不给分!
第(2)小问 2分 得到对称轴为y轴或者是 a = 0,1分
正确判断大小关系,1分
第(3)小问 3分 结论2分,答对一半或者多等号给1分
过程1分,必须有比较严谨(指出理论依据且有比较完整的推理过程)
2022/5/25
84
2022/5/25
85
6分
第26题·评卷样例
2022/5/25
87
6分
第26题·评卷样例
5分
第26题·评卷样例
5分
第26题·评卷样例
3分
第26题·评卷样例
3分
第26题·评卷样例
5分
4分
第26题·评卷样例
4分
第26题·评卷样例
4分
第26题·评卷样例
4分
第26题·评卷样例
第 27 题
2022/5/25
98
第27题·评分细则
第27题 满分 采分点及注意事项
第(1)小问① 2分 导出∠ABD=∠C,1分
完整证明,1分.
第(1)小问② 4分 画图1分,结论1分,证明2分.
证明中两组角都需要导出,
导出其中一组角可以得1分,完全证对可以得2分.
第(2)小问 1分 无争议
2022/5/25
99
随时关注补充的方法和细则!
注:三个全等条件必须列清楚!否则后面就不给分了.
第(1)①问中证明了AD=BE,在②问中必须要写出来(不用再证),否则不认为是三个条件全齐!
2022/5/25
100
第27题·评卷样例
2022/5/25
101
第 28 题
2022/5/25
102
第28题 满分 采分点及注意事项
第(1)小问 2分 无争议,有错不给分,少选且无错给1分.
第(2)小问 3分 结论2分,完全正确2分,对一半或者仅缺等号1分;
过程1分,有一定文字说理或者通过图形表述,得出两个端点之一即可
第(3)小问 2分 完全正确 2分
得1分的情况:①只写 r >√82,②只写 r =√82,有其他任何端点0分.
第28题·评分细则
第28题·评卷样例
3分
第28题·评卷样例
3分
第28题·评卷样例
3分
d
第28题·评卷样例
3分
第28题·评卷样例
3分
第28题·评卷样例
2分
第28题·评卷样例
3分
第28题·评卷样例
1分
要有文字!
1分
第28题·评卷样例
1分
1分
第28题·评卷样例
1分
感谢各位老师!
数学学科 评分细则及讲评建议
海淀区九年级第二学期期末练习
2022/5/25
1
一、命题立意
·以学定考,教、学、考一致
·以课标为纲,教材为抓手
·学考冲刺阶段的查缺补漏
2022/5/25
2
命题立意
严格依据课程标准命题。各地要认真落实依据义务教育课程标准命题的规定要求,坚决取消初中学业水平考试大纲或考试说明,不得超标命题和随意扩大、压减考试内容范围,严禁将高中课程内容、学科竞赛试题以及校外培训内容作为考试内容,确保依标命题、教考衔接。
科学设置试卷难度。各地要按照“两考合一”“兼顾毕业和升学”的功能定位,进一步对各相关学科中考试卷考试时长、容量、难度等提出规范要求,科学合理设置试卷难度,既要防止试卷过难增加学生学业负担,也要避免试卷过易难以体现区分度。要根据不同学科特点,合理设置试卷试题结构,减少记忆性试题,增加探究性、开放性、综合性试题,坚决防止偏题怪题,促进有效考查学生综合素质。
——教育部办公厅关于做好2022年中考命题工作的通知
2022/5/25
3
2022/5/25
4
命题立意
命题依据
以课标为纲
以教材为抓手
调研指向
命题原则
高频考点
回归课本
查缺补漏
诊断激励
素养立意,育人导向
核心素养
数学本质
通性通法
四基
四能
命题背景
双减
两考合一
疫情居家
2022/5/25
5
高频考点
整体规划
二模
一模
2022/5/25
6
对课本例题的简单改编
2022/5/25
7
从课本习题衍生,提炼数学思维
2022/5/25
8
第27题·命题立意
课本习题
把直线 l 转起来
变化的过程中
找最值
理解为绕点O的旋转
生成新的图形
逻辑推理的能力
探究与思考
二、评分细则与讲评建议
·基本原则:给分有理,扣分有据,严格遵循评标
·总体上既要让更多的学生有获得感,又体现适当的区分度
·在冲刺阶段,适当关注学生的作答规范
·关于建系、共圆等课本以外的知识,用对不扣分,用错不找
等价采分点,从用的那一步开始不记分.
2022/5/25
9
2022/5/25
10
来自技术的温馨提示
第 1-8 题
2022/5/25
11
选择题
2022/5/25
12
二模均分15.26
一模均分14.73
期末均分14.62
仍需夯实基础
对基础知识的掌握和落实
渐入佳境
2022/5/25
13
4.2%错选B
4.6%错选C
2021
2020
2022/5/25
14
数据的收集、整理与分析
数学与生活的紧密联系
第 9-16 题
2022/5/25
15
2022/5/25
16
9-16题评分原则:
1、除16题每空1分,其他题目只有0分和2分,每道题均为完全正确才可得2分.
2、所有结果只要正确,没化简不扣分.
3、第10题没有大括号也可以,但必须写出x,y对应来,单独写1,3不给分!
写成y1>y2满分.
4、第12题只要非正数即可.
5、第13题可以不写单位“°”
第9-16题·评分细则
2022/5/25
17
9-16题评分原则:
6、第14题注意只能加一个条件:例如AC⊥EF,AF=AE, AE=EC.
典型错误:AF=EC,AE=FC,AF=FC=CE=EA(这是几个条件)
写成理由的不给分.
注意区别:AC是FE的垂直平分线×,FE是AC的垂直平分线√
7、第16题② 不考虑顺序.
第9-16题·评分细则
2022/5/25
18
第16题·讲评建议
1、怎样提取有效信息?
2、“最少”怎样体现?
2020
总和30
最大值10(有两个)
第 17 题
2022/5/25
19
2022/5/25
20
17题评分原则:
1、共5分,四个计算各1分,结果1分;
2、若只写答案,只给答案1分;(以下同,仅答案对无合理过程只给答案分)
3、若学生抄了题,抄错且完全做对,可以给4分,抄题且做错,按4分上限,
依据上述规则扣分,没抄题的按原题判。
第17题·评分细则
2022/5/25
21
第17题·评卷样例
5分
4分
藏得挺深
2022/5/25
第17题·评卷样例
3分
2分
0分,全都不对也少见
第 18 题
2022/5/25
23
2022/5/25
24
18题评分原则:
1、共5分,每个不等式解对得2分,最后解集对1分;
2、若单个不等式解错,但去括号、去分母等步骤有对的,给相应的步骤分1分;
3、最后解集写成区间形式不扣分.
4、抄了题的学生,抄错题且完全做对的,给4分,但抄错题还做错,按4分上限根据上述规则扣分, 没抄题的按原题判。
第18题·评分细则
2022/5/25
第18题·评卷样例
4分
4分
0分,全都不对也少见
4分
4分 抄错题了
2022/5/25
第18题·评卷样例
3分,去分母对了
0分,没图
因为是自己上传
报问题卷也没用..
第 19 题
2022/5/25
27
2022/5/25
28
19题评分原则:
1、共6分,第(1)问3分,① 依题意△>0 或 判别式列对1分,
② 化对1分,③ 解对1分.
2、第(2)问3分,① 确定m=0,② 写出方程,或者列出求根公式
③ 解正确各1分.
第19题·评分细则
看错条件,△也没对,0分
第19题·评卷样例
列对、化对2分,m为0对,方程对2分,共4分
1’
1’
1’
1’
第19题·评卷样例
(1)列对1分(注意列对和△>0算一个点!),
(2)m=0对,方程对2分,共计3分
不规范,不扣分,讲评注意强调
1’
1’
1’
第19题·评卷样例
列错,△>0也没写出来,0分
第19题·评卷样例
第(1)问0分,第(2)问仅m=0给1分
1’
第19题·评卷样例
3’
1’
1’
第(2)问没有写出方程和求根公式之一,扣1分,3分+2分
第19题·评卷样例
第(2)问,m对,方程对,配方法解方程错,扣1分,3+2
3’
1’
1’
第19题·评卷样例
3’
1’
1’
没拍全,但可以基本合理推断他写对了,可以给满分
第19题·评卷样例
第 20 题
2022/5/25
37
2022/5/25
38
20题(1)评分原则:
1、证明共3分,有两种方法,①中位线→②平行四边形→③矩形
①中位线→②三个直角→③矩形
这两种证明方法每一步1分.
2、如果没有证明平行四边形,由两个平行+直角得矩形,扣1分(上次说的暂不
扣,这次要执行!),三个直角如果没有出全,酌情扣分.
第20题·评分细则
2022/5/25
39
20题(2)评分原则:
1、共3分,AC、AE、BE三条线段各1分;
第20题·评分细则
学生方法1:
平行四边形+90°→矩形
第20题·评卷样例
学生方法2:三个90°→矩形
第20题·评卷样例
利用两组对边相等证平行四边形时,但有跳步
利用三个90°证平行四边形,最后三个角没有写连等没问题
老师易判错的地方
没有出平行四边形就得矩形扣1分
跳步严重
很不规范
第20题·评卷样例
实在是太聒噪
第20题·评卷样例
第20题·评卷样例
不忍直视
第 21 题
2022/5/25
46
2022/5/25
47
21题(1)(2)评分原则:
1、(1)无争议,
2、(2)角平分线位置对且字母标记正确1分,作图痕迹1分;画错角分线不给分!
注意如果选a且∠BAE的平分线画对也给分,画成直线或者线段不扣分.
第21题·评分细则
2022/5/25
48
21题(3)评分原则:
1、写理由1分:整体意思对即可给分,笔误不扣分,但圆周角、圆心角、弧、
一半等关键词不承认笔误;
2、填角1分,无争议.
第21题·评分细则
2022/5/25
49
第21题·评卷样例
作角平分线
作中垂线由三线合一得角平分线
2022/5/25
50
第21题·评卷样例
直线、线段不扣分
没有尺规作图痕迹
扣1分
P点位置标错扣1分
特殊情况:
若第1问选a,第2问根据a的描述,正确尺规作出了∠BAE的平分线及点P
第1问,0分
第2问,2分
第21题·评卷样例
依据:0分示例
关键词不承认笔误,不给分,弧,圆周角,圆心角,一半
第21题·评卷样例
第 22 题
2022/5/25
53
2022/5/25
54
22题评分原则:
1、(1) 共3分,交点纵坐标、m、反比例函数解析式各占1分;总体来说解析式
对且y = 6对即可满分.
2、(2) 共2分,完全正确2分,仅得到k>2或者k=2得1分,其余0分.
注意:这里把 k ≥ 2 分成两个点来考虑,回答k ≤ 2的也算他踩到了k=2
第22题·评分细则
第 23 题
2022/5/25
55
2022/5/25
56
23题评分原则:
1、(1)画图 共2分,描出所有点1分,用平滑曲线连接1分
要连上每个点,平滑的曲线,不出头.(连直线不给分,出头扣1分)
2、(2)①②各1分,①无争议,② 允许的范围:95-105(含边界,取小数不扣分).
3、(3) 1分,无争议
第23题·评分细则
95-105含边界
第(1)问 画图 2分
① 描点正确1分;
② 连线正确1分.
2分 忽略连线的毛边
2分 点贴着线即可
2分 忽略空心实心点
第23题·评卷样例
2分 平滑曲线
趋势正确
第23题·评卷样例
1分 描点正确
连线不完整,出头
1分 描点正确
两端均出头
1分 描点正确
一端出头
1分 描点正确
连线不完整
第23题·评卷样例
0分 描点有错误
第23题·评卷样例
2022/5/25
61
函数探究问题
2015、16、20 给定解析式
2017、18、19 几何为背景
落脚点
·函数的概念
·函数的基本性质
·函数的应用(结合实际)
西城
2022/5/25
62
昌平二模
丰台
第 24 题
2022/5/25
63
第24题·评分细则
第24题 满分 采分点及注意事项
第(1)小问 2分 圆周角 or 等边对等角 1分,
平行线证明正确 1分
第(2)小问 4分 答案正确 两个答案各1分,共2分
证明任何一个30°、60°角或者证出等边三角形 1分
计算出AG(CG)、CD(AF)或者是其他等效线段长,1分
2022/5/25
64
注:本题的关键在于是否能够正确推出特殊角,
所以需要看过程,凡推理不合理的均应扣分.
凡因书写不规范导致难以理解的过程均酌情扣分.
第一问 2分满
第24题·评卷样例
第24题·评卷样例
第二问 4分满
标答+
第24题·评卷样例
第24题·评卷样例
第24题·评卷样例
第24题·评卷样例
求AC长时证全等
第24题·评卷样例
2分
证明平行四边形
2分
第24题·评卷样例
0分
第24题·评卷样例
1分
第24题·评卷样例
2分
4分
第24题·评卷样例
△CAE≌△DOE
第24题·评卷样例
第24题·评卷样例
2分
1分
第24题·评卷样例
第24题·评卷样例
第24题·评卷样例
第 25 题
2022/5/25
81
第25题·评分细则
五个点5分,
前四个点没有争议,理由必须表述严谨方可得分
2022/5/25
82
第 26 题
2022/5/25
83
第26题·评分细则
第26题 满分 采分点及注意事项
第(1)小问 1分 只写 a 不给分!
第(2)小问 2分 得到对称轴为y轴或者是 a = 0,1分
正确判断大小关系,1分
第(3)小问 3分 结论2分,答对一半或者多等号给1分
过程1分,必须有比较严谨(指出理论依据且有比较完整的推理过程)
2022/5/25
84
2022/5/25
85
6分
第26题·评卷样例
2022/5/25
87
6分
第26题·评卷样例
5分
第26题·评卷样例
5分
第26题·评卷样例
3分
第26题·评卷样例
3分
第26题·评卷样例
5分
4分
第26题·评卷样例
4分
第26题·评卷样例
4分
第26题·评卷样例
4分
第26题·评卷样例
第 27 题
2022/5/25
98
第27题·评分细则
第27题 满分 采分点及注意事项
第(1)小问① 2分 导出∠ABD=∠C,1分
完整证明,1分.
第(1)小问② 4分 画图1分,结论1分,证明2分.
证明中两组角都需要导出,
导出其中一组角可以得1分,完全证对可以得2分.
第(2)小问 1分 无争议
2022/5/25
99
随时关注补充的方法和细则!
注:三个全等条件必须列清楚!否则后面就不给分了.
第(1)①问中证明了AD=BE,在②问中必须要写出来(不用再证),否则不认为是三个条件全齐!
2022/5/25
100
第27题·评卷样例
2022/5/25
101
第 28 题
2022/5/25
102
第28题 满分 采分点及注意事项
第(1)小问 2分 无争议,有错不给分,少选且无错给1分.
第(2)小问 3分 结论2分,完全正确2分,对一半或者仅缺等号1分;
过程1分,有一定文字说理或者通过图形表述,得出两个端点之一即可
第(3)小问 2分 完全正确 2分
得1分的情况:①只写 r >√82,②只写 r =√82,有其他任何端点0分.
第28题·评分细则
第28题·评卷样例
3分
第28题·评卷样例
3分
第28题·评卷样例
3分
d
第28题·评卷样例
3分
第28题·评卷样例
3分
第28题·评卷样例
2分
第28题·评卷样例
3分
第28题·评卷样例
1分
要有文字!
1分
第28题·评卷样例
1分
1分
第28题·评卷样例
1分
感谢各位老师!
同课章节目录
