18.1平行四边形 期末复习综合练习题 2021-2022学年人教版八年级数学下册(word版含答案)
文档属性
| 名称 | 18.1平行四边形 期末复习综合练习题 2021-2022学年人教版八年级数学下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 369.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 17:28:54 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学下册《18.1平行四边形》期末复习综合练习题(附答案)
一.选择题
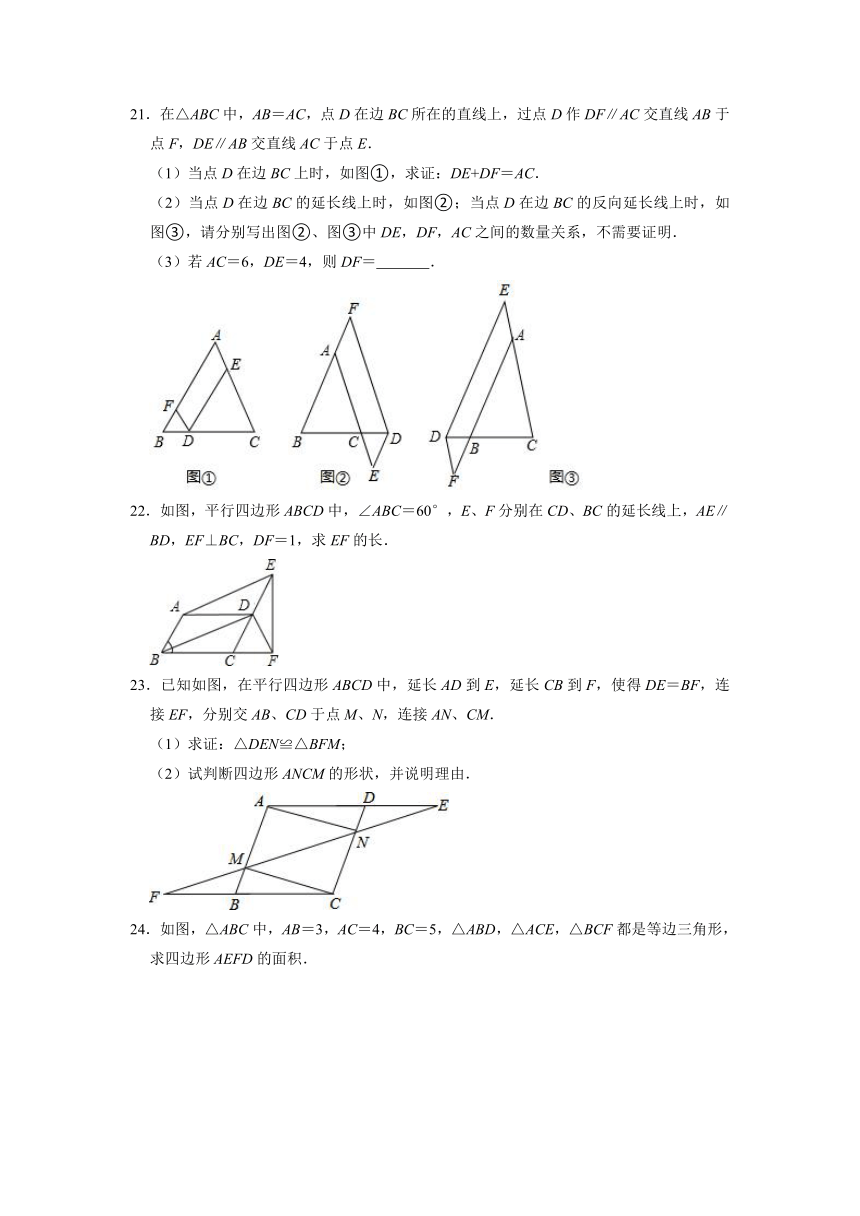
1.如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( )
A.6 B.8 C.10 D.13
2.如图,平行四边形ABCD的对角线AC,BD交于点O,AB=,∠AOB=60°,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+2EF的值为( )
A.+1 B. C. D.
3.如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形;②AB=BC;③AC⊥BD④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
4.如图,在 ABCD中,E是AD边的中点,BE平分∠ABC.若AB=2,则 ABCD的周长是( )
A.11 B.12 C.13 D.14
5.如图,AB∥CD,AD∥BC,AE∥CF,B,E,F,D在同一直线上.则图中的全等三角形有( )
A.一对 B.二对 C.三对 D.四对
6.如图,已知 ABCD三个顶点坐标是A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),那么第四个顶点D的坐标是( )
A.(3,1) B.(3,2) C.(3,3) D.(3,4)
7.如图,已知△ABC中AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④∠DAE=90°.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
8.如图,在 ABCD中,AD>AB,以点A为圆心,AB为半径画弧与AD交于点F,然后分别以B,F为圆心,大于为半径画弧交于点G,连接AG交BC于点E,若BF=6,AB=4,则AE的长为( )
A. B.2 C.5 D.10
二.填空题
9.在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,M是BC上一点,且BM=4cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,当t的值为 时,以A、M、E、F为顶点的四边形是平行四边形.
10.如图,在平行四边形ABCD中,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,当点D,F,E,C相邻两点间的距离相等时,则的值为 .
11.如图,平行四边形ABCD中,BD为对角线,∠C=60°,BE平分∠ABC交DC于点E,连接AE,若∠EAB=38°,则∠DBE为 度.
12.如图,在 ABCD中,AE=2,AD=5,∠BCD的平分线与BA的延长线相交于点E,则CD的长为 .
13.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=17cm2,S△BQC=27cm2,则阴影部分的面积为 cm2.
14.如图,点O是 ABCD的对角线交点,E为CD中点,AE交BD于点F,若S△AOE=3,则S△AOB的值为 .
15.如图,在 ABCD中,AC=BC,∠CAD=40°,BE⊥AC于点E,则∠ABE的度数为 .
16.在 ABCD中,∠BAD的平分线把BC边分成长度是4和6的两部分,则 ABCD的周长是 .
17.在平面直角坐标系中, OABC的顶点O,B的坐标分别为(0,0)、,点A在x轴上且∠AOC=60°,则点A的坐标为 .
三.解答题
18.如图所示,△ABC≌△EAD,点E在BC上.
(1)求证:四边形ABCD是平行四边形;
(2)若∠B:∠CAD=5:4,AE⊥ED,求∠EDC的度数.
19.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
20.如图,在 ABCD中,点M、N分别在边AD、BC上,点E、F在对角线BD上,且DM=BN,BE=DF.
(1)求证:四边形ENFM是平行四边形.
(2)若点M是AD中点,AB=4,MF=1,∠EMF=90°,则EM= .
21.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
22.如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BC,DF=1,求EF的长.
23.已知如图,在平行四边形ABCD中,延长AD到E,延长CB到F,使得DE=BF,连接EF,分别交AB、CD于点M、N,连接AN、CM.
(1)求证:△DEN≌△BFM;
(2)试判断四边形ANCM的形状,并说明理由.
24.如图,△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,求四边形AEFD的面积.
参考答案
一.选择题
1.解:如图,设BE与FC的交点为H,过点A作AM∥FC,交BE与点O,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ABC+∠DCB+180°,
∵BE平分∠ABC,CF平分∠BCD,
∴∠ABE=∠EBC,∠BCF=∠DCF,
∴∠CBE+∠BCF=90°,
∴∠BHC=90°,
∵AM∥CF,
∴∠AOE=∠BHC=90°,
∵AD∥BC,
∴∠AEB=∠EBC=∠ABE,
∴AB=AE=5,
又∵∠AOE=90°,
∴BO=OE=3,
∴AO=,
在△ABO和△MBO中,
,
∴△ABO≌△MBO(ASA),
∴AO=OM=4,
∴AM=8,
∵AD∥BC,AM∥CF,
∴四边形AMCF是平行四边形,
∴CF=AM=8,
故选:B.
2.解:∵∠BAO=90°,∠AOB=60°,
∴∠ABO=30°,
∴BO=2AO,
∵AB=,
∴AO=1,BO=2,
∴S△ABO=AO AB=,
∵四边形ABCD为平行四边形,
∴DO=BO=2,S△ADO=S△ABO=,
∵OF⊥AO,EF⊥OD,
∴S△ADO=S△AEO+S△EDO===,
即OE+2EF=.
故选:B.
3.解:∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,故①正确;
∵AD=DC,
∴平行四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AC平分∠BAD,故②③④正确,
∵AC=6,BD=8,
∴菱形ABCD的面积=AC×BD=×6×8=24,故⑤正确;
正确的个数有5个,故选:D.
4.解:∵ABCD为平行四边形,
∴AD∥BC,∠AEB=∠EBC,
又BE平分∠ABC,∠ABE=∠AEB,
故△ABE为等腰三角形,
∴AE=AB=2,可知AD=4,
∴ ABCD的周长=2(AB+AD)=12.故选:B.
5.解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
则图中全等的三角形有:△ABE≌△CDF,△ADE≌△CBF,△ABD≌△CDB,共3对.
故选:C.
6.解:
过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,
则四边形EFNM是矩形,
所以EF=MN,EM=FN,FN∥EM,
∴∠EAB=∠AQC,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠AQC=∠DCN,
∴∠DCN=∠EAB,
在△DCN和△BAE中
,
∴△DCN≌△BAE(AAS),
∴BE=DN,AE=CN,
∵A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),
∴CN=AE=2﹣1=1,DN=BE=3,
∴DM=3﹣1=2,OM=2+1=3,
∴D的坐标为(3,2),故选:B.
7.解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴∠DAE=90°,故④正确;
∵AE=BD=BC,AG=AC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
8.解:设AE交BF于点O,连接EF,如图所示:
由题意可知:AB=AF,AE⊥BF,
∴OB=OF,∠BAE=∠EAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=AF,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴OA=OE,OB=OF=BF=3,
在Rt△AOB中,OA=,
∴AE=2OA=2,
故选:B.
二.填空题
9.解:分两种情况:
①当点F在线段BM上,即0≤t<2,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=4﹣2t,
解得:t=;
②当F在线段CM上,即2≤t≤5,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=2t﹣4,
解得:t=4,
综上所述,t=s或4s时,以A、M、E、F为顶点的四边形是平行四边形,
故答案为:s或4s.
10.解:∵四边形ABCD是平行四边形,
∴CD=AB,BC=AD=5,AB∥CD,
∴∠DEA=∠BAE,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DEA=∠DAE,
∴DE=AD,
同理BC=CF,分三种情况:
①如图3所示:
同(1)得:AD=DE,
∵点C,D,E,F相邻两点间的距离相等,
∴AD=DE=EF=CF,
∴的值为;
②如图2所示:
同(1)得:AD=DE=CF,
∵DF=FE=CE,
∴的值为;
③如图3所示:
同(1)得:AD=DE=CF,
∵DF=DC=CE,
∴的值为2;
综上所述,的值为或或2,
故答案为:或或2.
11.解:∵平行四边形ABCD中,∠C=60°,
∴AD=BC,∠ADE=∠ABC=120°,∠BAD=60°,
∵∠EAB=38°,
∴∠EAD=∠BAD﹣∠EAB=22°,
∵BE平分∠ABC,
∴∠CBE=60°,
∴△BCE是等边三角形,
∴BE=BC,∠BEC=60°,
∴BE=AD,∠BED=120°=∠ADE,
在△BDE与△AED中,
,
∴△BDE≌△AED(SAS),
∴∠DBE=∠EAD=22°,
故答案为:22.
12.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=5,
∴∠E=∠DCE,
∵CE是∠BCD的平分线,
∴∠BCE=∠DCE,
∴∠E=∠BCE,
∴BE=BC=5,
∴CD=AB=BE﹣AE=5﹣2=3,
故答案为:3.
13.解:如图,连接EF
∵△ADF与△DEF同底等高,
∴S△ADF=S△DEF,
即S△ADF﹣S△DPF=S△DEF﹣S△DPF,
即S△APD=S△EPF=17cm2,
同理可得S△BQC=S△EFQ=27cm2,
∴阴影部分的面积为S△EPF+S△EFQ=17+27=44cm2.
故答案为:44.
14.解:∵点O是 ABCD的对角线交点,
∴O是AC的中点,则S△AOE=S△EOC,
又∵E为CD中点,
∴EO是△ACD的中位线,
∴EO∥AD,
∴S△AOE=S△DOE,
∴S△DOC=3+3=6,
故S△AOB的值为6.
故答案为:6.
15.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CAD=∠ACB=40°,
∵AC=BC,
∴∠BAE=∠ABC=,
∵BE⊥AC,
∴∠BEA=90°,
∴∠ABE=90°﹣∠BAC=90°﹣70°=20°,
故答案为:20°.
16.解:在平行四边形ABCD中,AD∥BC,则∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,BC=BE+EC,
①当BE=4,EC=6时,
平行四边形ABCD的周长为:2(AB+AD)=2(4+4+6)=28.
②当BE=6,EC=4时,
平行四边形ABCD的周长为:2(AB+AD)=2(6+6+4)=32.
故答案为:28或32.
17.解:∵ OABC的顶点O,B的坐标分别为(0,0)、(5,),点A在x轴上,∠AOC=60°,
过点B作BE⊥OA,交OA的延长线于E,
∴∠BAE=∠AOC=60°,BE=,
∴AE=1,
∴点A的坐标为(4,0),
故答案为:(4,0).
三.解答题
18.(1)证明:∵△ABC≌△EAD,
∴AD=BC,AB=AE,∠B=∠DAE,
∴∠B=∠AEB,
∴∠DAE=∠AEB,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)解:由(1)知AD∥BC,
∴∠CAD=∠ACB,
∵∠B:∠CAD=5:4,
∴∠B:∠ACB=5:4,
设∠B=5x,∠ACB=4x,
∵AE⊥ED,
∴∠AED=90°,
∵△ABC≌△EAD,
∴∠BAC=∠AED=90°,
∴∠B+∠ACB=90°,
∴5x+4x=90°,
∴x=10°,
∴∠B=∠ADC=50°,∠ADE=∠ACB=4x=40°,
∴∠EDC=10°.
19.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODF=∠OBE,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(AAS),
∴DF=BE,
∴AD﹣DF=BC﹣BE,
即AF=EC,
∴四边形AECF为平行四边形.
20.(1)证明:在平行四边形ABCD中,AD∥BC,
∴∠ADB=∠CBD.
在△BNE和△DMF中,
,
∴△BNE≌△DMF(SAS).
∴MF=NE,∠DFM=∠BEN.
∴EN∥FM.
∴四边形ENFM是平行四边形;
(2)连接MN,
由(1)知,四边形ENFM是平行四边形,
∵∠EMF=90°,
∴四边形ENFM是矩形,
∴MN=EF,
∵点M是AD中点,
∴AM=DM,
∵四边形ABCD是平行四边形,
∴AD=BC,
∵DM=BN,
∴AM=BN,
∴四边形ABNM是矩形,
∴MN=AB=4,
∵MF=1,
∴EM===,
故答案为:.
21.解:(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∴AF=DE,
∵DF∥AC,
∴∠FDB=∠C
又∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B
∴DF=BF
∴DE+DF=AB=AC;
(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC﹣DE=6﹣4=2;
当如图②的情况,DF=AC+DE=6+4=10.
故答案是:2或10.
22.解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∴CE=2DF=2,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,∴,
在Rt△CEF中,由勾股定理得:.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AE∥CF,∠ADC=∠ABC,
∴∠E=∠F,∠EDN=∠FBM,
∴在△DEN与△BFM中,,
∴△DEN≌△BFM(ASA).
(2)解:四边形ANCM是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD即AM∥CN.
又由(1)知,△DEN≌△BFM,
∴AM=CN,
∴四边形ANCM是平行四边形.
24.解:∵如图,△ABC中,AB=3,AC=4,BC=5,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°.
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证△ABC≌△EFC,
∴AB=EF=AD=3,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°﹣∠DAE=30°,
∴S AEFD=3×(4×)=6.
答四边形AEFD的面积是6.
一.选择题
1.如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( )
A.6 B.8 C.10 D.13
2.如图,平行四边形ABCD的对角线AC,BD交于点O,AB=,∠AOB=60°,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+2EF的值为( )
A.+1 B. C. D.
3.如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形;②AB=BC;③AC⊥BD④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
4.如图,在 ABCD中,E是AD边的中点,BE平分∠ABC.若AB=2,则 ABCD的周长是( )
A.11 B.12 C.13 D.14
5.如图,AB∥CD,AD∥BC,AE∥CF,B,E,F,D在同一直线上.则图中的全等三角形有( )
A.一对 B.二对 C.三对 D.四对
6.如图,已知 ABCD三个顶点坐标是A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),那么第四个顶点D的坐标是( )
A.(3,1) B.(3,2) C.(3,3) D.(3,4)
7.如图,已知△ABC中AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④∠DAE=90°.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
8.如图,在 ABCD中,AD>AB,以点A为圆心,AB为半径画弧与AD交于点F,然后分别以B,F为圆心,大于为半径画弧交于点G,连接AG交BC于点E,若BF=6,AB=4,则AE的长为( )
A. B.2 C.5 D.10
二.填空题
9.在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,M是BC上一点,且BM=4cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,当t的值为 时,以A、M、E、F为顶点的四边形是平行四边形.
10.如图,在平行四边形ABCD中,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,当点D,F,E,C相邻两点间的距离相等时,则的值为 .
11.如图,平行四边形ABCD中,BD为对角线,∠C=60°,BE平分∠ABC交DC于点E,连接AE,若∠EAB=38°,则∠DBE为 度.
12.如图,在 ABCD中,AE=2,AD=5,∠BCD的平分线与BA的延长线相交于点E,则CD的长为 .
13.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=17cm2,S△BQC=27cm2,则阴影部分的面积为 cm2.
14.如图,点O是 ABCD的对角线交点,E为CD中点,AE交BD于点F,若S△AOE=3,则S△AOB的值为 .
15.如图,在 ABCD中,AC=BC,∠CAD=40°,BE⊥AC于点E,则∠ABE的度数为 .
16.在 ABCD中,∠BAD的平分线把BC边分成长度是4和6的两部分,则 ABCD的周长是 .
17.在平面直角坐标系中, OABC的顶点O,B的坐标分别为(0,0)、,点A在x轴上且∠AOC=60°,则点A的坐标为 .
三.解答题
18.如图所示,△ABC≌△EAD,点E在BC上.
(1)求证:四边形ABCD是平行四边形;
(2)若∠B:∠CAD=5:4,AE⊥ED,求∠EDC的度数.
19.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
20.如图,在 ABCD中,点M、N分别在边AD、BC上,点E、F在对角线BD上,且DM=BN,BE=DF.
(1)求证:四边形ENFM是平行四边形.
(2)若点M是AD中点,AB=4,MF=1,∠EMF=90°,则EM= .
21.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
22.如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BC,DF=1,求EF的长.
23.已知如图,在平行四边形ABCD中,延长AD到E,延长CB到F,使得DE=BF,连接EF,分别交AB、CD于点M、N,连接AN、CM.
(1)求证:△DEN≌△BFM;
(2)试判断四边形ANCM的形状,并说明理由.
24.如图,△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,求四边形AEFD的面积.
参考答案
一.选择题
1.解:如图,设BE与FC的交点为H,过点A作AM∥FC,交BE与点O,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ABC+∠DCB+180°,
∵BE平分∠ABC,CF平分∠BCD,
∴∠ABE=∠EBC,∠BCF=∠DCF,
∴∠CBE+∠BCF=90°,
∴∠BHC=90°,
∵AM∥CF,
∴∠AOE=∠BHC=90°,
∵AD∥BC,
∴∠AEB=∠EBC=∠ABE,
∴AB=AE=5,
又∵∠AOE=90°,
∴BO=OE=3,
∴AO=,
在△ABO和△MBO中,
,
∴△ABO≌△MBO(ASA),
∴AO=OM=4,
∴AM=8,
∵AD∥BC,AM∥CF,
∴四边形AMCF是平行四边形,
∴CF=AM=8,
故选:B.
2.解:∵∠BAO=90°,∠AOB=60°,
∴∠ABO=30°,
∴BO=2AO,
∵AB=,
∴AO=1,BO=2,
∴S△ABO=AO AB=,
∵四边形ABCD为平行四边形,
∴DO=BO=2,S△ADO=S△ABO=,
∵OF⊥AO,EF⊥OD,
∴S△ADO=S△AEO+S△EDO===,
即OE+2EF=.
故选:B.
3.解:∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,故①正确;
∵AD=DC,
∴平行四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AC平分∠BAD,故②③④正确,
∵AC=6,BD=8,
∴菱形ABCD的面积=AC×BD=×6×8=24,故⑤正确;
正确的个数有5个,故选:D.
4.解:∵ABCD为平行四边形,
∴AD∥BC,∠AEB=∠EBC,
又BE平分∠ABC,∠ABE=∠AEB,
故△ABE为等腰三角形,
∴AE=AB=2,可知AD=4,
∴ ABCD的周长=2(AB+AD)=12.故选:B.
5.解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
则图中全等的三角形有:△ABE≌△CDF,△ADE≌△CBF,△ABD≌△CDB,共3对.
故选:C.
6.解:
过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,
则四边形EFNM是矩形,
所以EF=MN,EM=FN,FN∥EM,
∴∠EAB=∠AQC,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠AQC=∠DCN,
∴∠DCN=∠EAB,
在△DCN和△BAE中
,
∴△DCN≌△BAE(AAS),
∴BE=DN,AE=CN,
∵A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),
∴CN=AE=2﹣1=1,DN=BE=3,
∴DM=3﹣1=2,OM=2+1=3,
∴D的坐标为(3,2),故选:B.
7.解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴∠DAE=90°,故④正确;
∵AE=BD=BC,AG=AC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
8.解:设AE交BF于点O,连接EF,如图所示:
由题意可知:AB=AF,AE⊥BF,
∴OB=OF,∠BAE=∠EAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=AF,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴OA=OE,OB=OF=BF=3,
在Rt△AOB中,OA=,
∴AE=2OA=2,
故选:B.
二.填空题
9.解:分两种情况:
①当点F在线段BM上,即0≤t<2,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=4﹣2t,
解得:t=;
②当F在线段CM上,即2≤t≤5,AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,
则有t=2t﹣4,
解得:t=4,
综上所述,t=s或4s时,以A、M、E、F为顶点的四边形是平行四边形,
故答案为:s或4s.
10.解:∵四边形ABCD是平行四边形,
∴CD=AB,BC=AD=5,AB∥CD,
∴∠DEA=∠BAE,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DEA=∠DAE,
∴DE=AD,
同理BC=CF,分三种情况:
①如图3所示:
同(1)得:AD=DE,
∵点C,D,E,F相邻两点间的距离相等,
∴AD=DE=EF=CF,
∴的值为;
②如图2所示:
同(1)得:AD=DE=CF,
∵DF=FE=CE,
∴的值为;
③如图3所示:
同(1)得:AD=DE=CF,
∵DF=DC=CE,
∴的值为2;
综上所述,的值为或或2,
故答案为:或或2.
11.解:∵平行四边形ABCD中,∠C=60°,
∴AD=BC,∠ADE=∠ABC=120°,∠BAD=60°,
∵∠EAB=38°,
∴∠EAD=∠BAD﹣∠EAB=22°,
∵BE平分∠ABC,
∴∠CBE=60°,
∴△BCE是等边三角形,
∴BE=BC,∠BEC=60°,
∴BE=AD,∠BED=120°=∠ADE,
在△BDE与△AED中,
,
∴△BDE≌△AED(SAS),
∴∠DBE=∠EAD=22°,
故答案为:22.
12.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=5,
∴∠E=∠DCE,
∵CE是∠BCD的平分线,
∴∠BCE=∠DCE,
∴∠E=∠BCE,
∴BE=BC=5,
∴CD=AB=BE﹣AE=5﹣2=3,
故答案为:3.
13.解:如图,连接EF
∵△ADF与△DEF同底等高,
∴S△ADF=S△DEF,
即S△ADF﹣S△DPF=S△DEF﹣S△DPF,
即S△APD=S△EPF=17cm2,
同理可得S△BQC=S△EFQ=27cm2,
∴阴影部分的面积为S△EPF+S△EFQ=17+27=44cm2.
故答案为:44.
14.解:∵点O是 ABCD的对角线交点,
∴O是AC的中点,则S△AOE=S△EOC,
又∵E为CD中点,
∴EO是△ACD的中位线,
∴EO∥AD,
∴S△AOE=S△DOE,
∴S△DOC=3+3=6,
故S△AOB的值为6.
故答案为:6.
15.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CAD=∠ACB=40°,
∵AC=BC,
∴∠BAE=∠ABC=,
∵BE⊥AC,
∴∠BEA=90°,
∴∠ABE=90°﹣∠BAC=90°﹣70°=20°,
故答案为:20°.
16.解:在平行四边形ABCD中,AD∥BC,则∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,BC=BE+EC,
①当BE=4,EC=6时,
平行四边形ABCD的周长为:2(AB+AD)=2(4+4+6)=28.
②当BE=6,EC=4时,
平行四边形ABCD的周长为:2(AB+AD)=2(6+6+4)=32.
故答案为:28或32.
17.解:∵ OABC的顶点O,B的坐标分别为(0,0)、(5,),点A在x轴上,∠AOC=60°,
过点B作BE⊥OA,交OA的延长线于E,
∴∠BAE=∠AOC=60°,BE=,
∴AE=1,
∴点A的坐标为(4,0),
故答案为:(4,0).
三.解答题
18.(1)证明:∵△ABC≌△EAD,
∴AD=BC,AB=AE,∠B=∠DAE,
∴∠B=∠AEB,
∴∠DAE=∠AEB,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)解:由(1)知AD∥BC,
∴∠CAD=∠ACB,
∵∠B:∠CAD=5:4,
∴∠B:∠ACB=5:4,
设∠B=5x,∠ACB=4x,
∵AE⊥ED,
∴∠AED=90°,
∵△ABC≌△EAD,
∴∠BAC=∠AED=90°,
∴∠B+∠ACB=90°,
∴5x+4x=90°,
∴x=10°,
∴∠B=∠ADC=50°,∠ADE=∠ACB=4x=40°,
∴∠EDC=10°.
19.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODF=∠OBE,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(AAS),
∴DF=BE,
∴AD﹣DF=BC﹣BE,
即AF=EC,
∴四边形AECF为平行四边形.
20.(1)证明:在平行四边形ABCD中,AD∥BC,
∴∠ADB=∠CBD.
在△BNE和△DMF中,
,
∴△BNE≌△DMF(SAS).
∴MF=NE,∠DFM=∠BEN.
∴EN∥FM.
∴四边形ENFM是平行四边形;
(2)连接MN,
由(1)知,四边形ENFM是平行四边形,
∵∠EMF=90°,
∴四边形ENFM是矩形,
∴MN=EF,
∵点M是AD中点,
∴AM=DM,
∵四边形ABCD是平行四边形,
∴AD=BC,
∵DM=BN,
∴AM=BN,
∴四边形ABNM是矩形,
∴MN=AB=4,
∵MF=1,
∴EM===,
故答案为:.
21.解:(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∴AF=DE,
∵DF∥AC,
∴∠FDB=∠C
又∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B
∴DF=BF
∴DE+DF=AB=AC;
(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC﹣DE=6﹣4=2;
当如图②的情况,DF=AC+DE=6+4=10.
故答案是:2或10.
22.解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∴CE=2DF=2,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,∴,
在Rt△CEF中,由勾股定理得:.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AE∥CF,∠ADC=∠ABC,
∴∠E=∠F,∠EDN=∠FBM,
∴在△DEN与△BFM中,,
∴△DEN≌△BFM(ASA).
(2)解:四边形ANCM是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD即AM∥CN.
又由(1)知,△DEN≌△BFM,
∴AM=CN,
∴四边形ANCM是平行四边形.
24.解:∵如图,△ABC中,AB=3,AC=4,BC=5,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°.
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证△ABC≌△EFC,
∴AB=EF=AD=3,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°﹣∠DAE=30°,
∴S AEFD=3×(4×)=6.
答四边形AEFD的面积是6.
