一元二次方程根与系数的关系

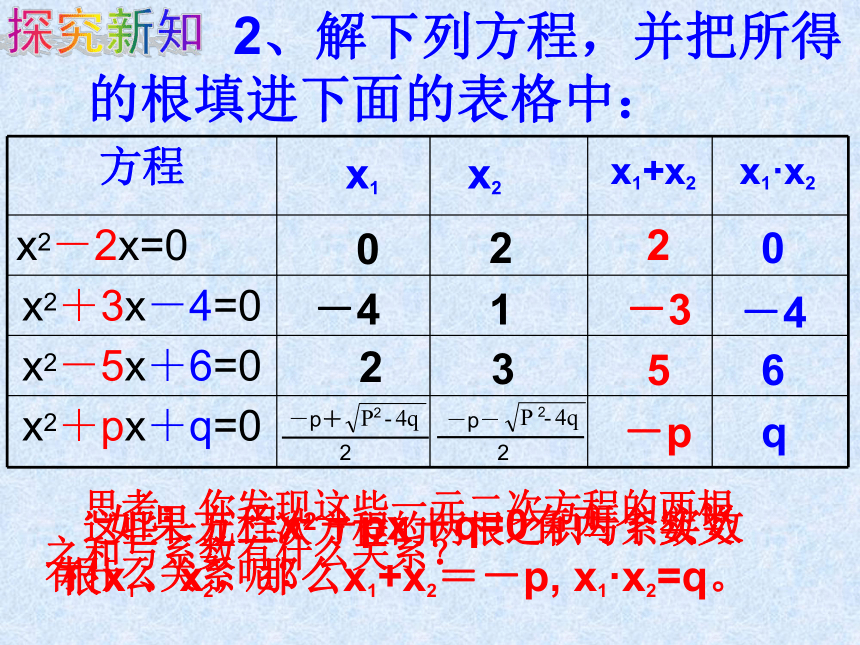
课件15张PPT。光荣中学：罗东实践与探索（三）根与系数的关系（1）一元二次方程温故知新ax2＋bx＋c=0( )， 1、一元二次方程的一般形式是它的两根分别是a≠0 这些一元二次方程的两根之积与系数又有什么关系呢？ 2、解下列方程，并把所得的根填进下面的表格中：0221－402－3－4356q－px1x2x1·x2x1+x2 如果方程x2＋px＋q=0有两个实数根x1、x2，那么x1+x2＝－p, x1·x2=q。 探究新知 思考：你发现这些一元二次方程的两根之和与系数有什么关系？ 不解方程，直接说出下列各方程两根之和与两根之积。 1、x2－7x－2=0
2、x2＋3x=0
3、x2－x=2小试牛刀2x2＋5x+3=0 观察下列关于X的方程， 思考：它们的两根之和、两根之积与系数有什么关系？x2＋ x+ =0x2＋ x+ =0ax2＋bx+c=0(a≠0)x1+x2 x1·x2 如果方程ax2＋bx＋c=0(a≠0)有两个实数
根x1、x2，那么x1+x2＝ , x1·x2= 。=例1：填空1、方程x2－4x＋1=0的两根之
和是 ，两根之积是 。
2、方程2x2－3x=4的两根之和
是 ，两根之积是 。新知运用1、填空：方程2x2＋3x－1=0的两根之和
是 ，两根之积是 。
2、选择：关于x的方程x2－2x＋m=0的两根之积为0,则m＝（ ）。
A、2 B、0
C、1 D、不确定 大胆尝试 例2：若x1、x2是方程x2－3x－1=0的两个根，不解方程求下列各式的值。
（1） x12x2＋x1x22 （2）x12＋x22
继续前进(1)解：由根与系数的关系得：
x1+x2=3, x1·x2=-1∴ x12x2＋x1x22＝x1x2(x1+x2)＝ -1×3
＝-3 例2：若x1、x2是方程x2－3x－1=0的两个根，不解方程求下列各式的值。
（2）x12＋x22
继续前进(2)解：由根与系数的关系得： x1+x2=3, x1·x2=-1∴ x12＋x22 ＝x12＋2x1x2＋x22－2x1x2＝ (x1＋x2)2－ 2x1x2 ＝32－2×(-1)
＝11 若m、n是方程2x2＋4x－6=0的两个根，不解方程求下列各式的值。学以致用1、知识:谈谈收获2、方法:自我检测1、填空：
（1）方程x2-3x+1=0的两根之和是 ，两根之积
是 。
（2）已知α，β是方程2x2+3x=0的两个根，那么
α+β=_____α·β=_____ 。
2、若方程y2＋by－4=0的两根恰好互为相反数，则b的值为( )。
A、2 B、－2 C、0 D、无法确定
3、已知a、b是方程2x2＋6x+3=0的两个实数根，求下列各式的值：

（1）（a+1)(b+1) (2) (a-b)2 已知a、b是方程2x2＋6x＋3=0的两个实数根，求下列各式的值。
（1） ＋
（2）(a－2)(b－2)
（3） ＋作业感谢各位老师莅临指导！