圆的对称性(1)
图片预览

文档简介
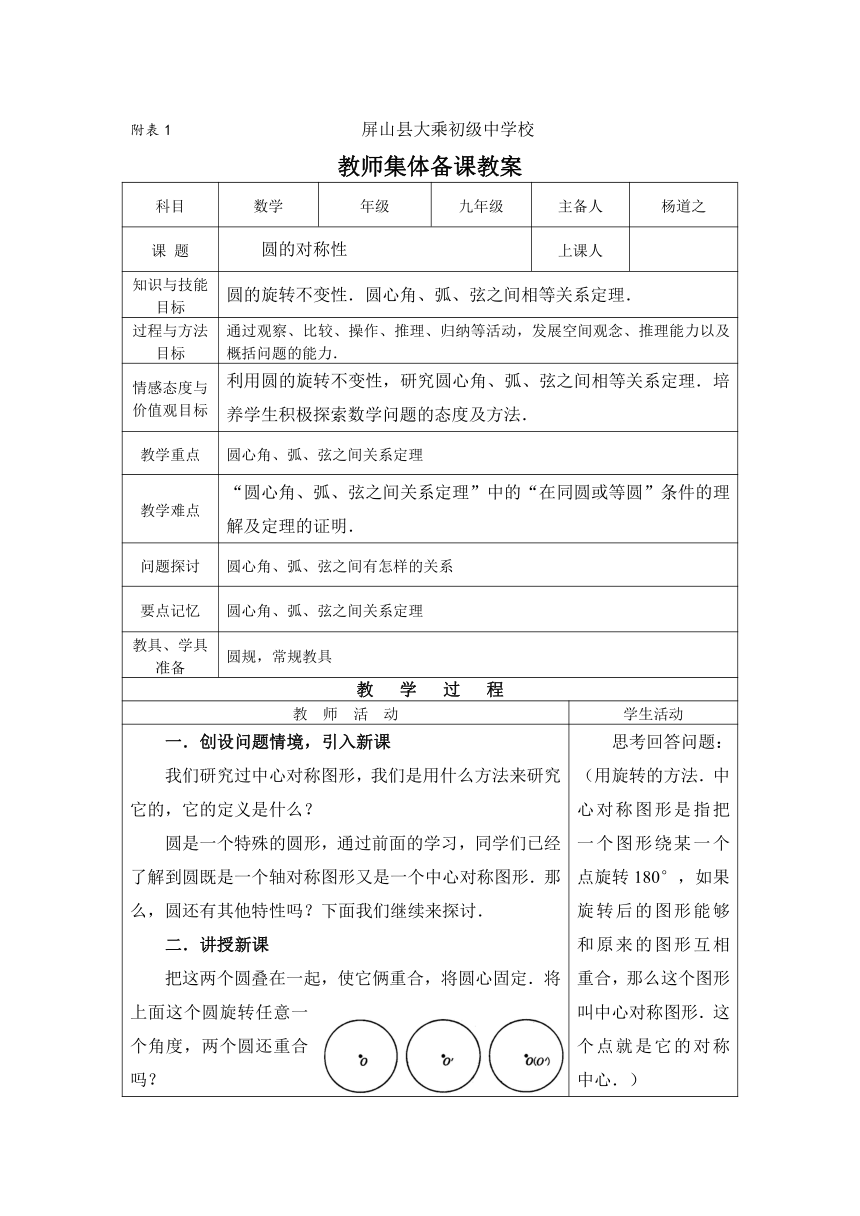
附表1 屏山县大乘初级中学校
教师集体备课教案
科目 数学 年级 九年级 主备人 杨道之
课 题 圆的对称性 上课人
知识与技能目标 圆的旋转不变性.圆心角、弧、弦之间相等关系定理.
过程与方法目标 通过观察、比较、操作、推理、归纳等活动,发展空间观念、推理能力以及概括问题的能力.
情感态度与价值观目标 利用圆的旋转不变性,研究圆心角、弧、弦之间相等关系定理.培养学生积极探索数学问题的态度及方法.
教学重点 圆心角、弧、弦之间关系定理
教学难点 “圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明.
问题探讨 圆心角、弧、弦之间有怎样的关系
要点记忆 圆心角、弧、弦之间关系定理
教具、学具准备 圆规,常规教具
教 学 过 程
教 师 活 动 学生活动
一.创设问题情境,引入新课我们研究过中心对称图形,我们是用什么方法来研究它的,它的定义是什么?圆是一个特殊的圆形,通过前面的学习,同学们已经了解到圆既是一个轴对称图形又是一个中心对称图形.那么,圆还有其他特性吗?下面我们继续来探讨.二.讲授新课把这两个圆叠在一起,使它俩重合,将圆心固定.将上面这个圆旋转任意一个角度,两个圆还重合吗?通过旋转的方法我们知道:圆具有旋转不变的特性.即一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.圆的中心对称性是其旋转不变性的特例.即圆是中心对称图形,对称中心为圆心.按下面的步骤做一做:1.在两张透明纸上,作两个半径相等的⊙O和⊙O′,沿圆周分别将两圆剪下.2.在⊙O和⊙O'上分别作相等的圆心角∠AOB和∠A'O'B'(如下图示),圆心固定.注意:在画∠AOB与∠A'O'B'时,要使OB相对于OA的方向与O'B'相对于O'A'的方向一致,否则当OA与OA'重合时,OB与O'B'不能重合.3.将其中的一个圆旋转一个角度,使得OA与O'A'重合.由已知条件可知∠AOB=∠A'O'B'.由两圆的半径相等,可以得到∠OAB=∠OBA=∠O'A'B'=∠O'B'A'.由△AOB≌△A'O'B',可得到AB=A'B'.由旋转法可知.……我们在上述做一做的过程中发现,固定圆心,将其中一个圆旋转一个角度,使半径OA与O'A'重合时,由于∠AOB=∠A'O'B'.这样便得到半径OB与O'B'重合.因为点A和点A'重合,点B和点B'重合,所以和重合,弦AB与弦A'B'重合,即,AB=A'B'.如上图所示,已知:⊙O和⊙O'是两个半径相等的圆,∠AOB=∠A'O'B'.求证:,AB=A'B'.上面的结论,在同圆中也成立.于是得到下面的定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等3、例题讲解如下图,⊙O的直径AB=10cm,C为⊙O上的一点,∠ABC=30°,求AC的长.解:∵AB为⊙O的直径.∴∠ACB=90°.又∵∠ABC=30°,∴AC=AB=×10=5(cm).4.课时小结5.课后作业 思考回答问题:(用旋转的方法.中心对称图形是指把一个图形绕某一个点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫中心对称图形.这个点就是它的对称中心.)观察两个圆有什么特点?动手操作通过上面的做一做,你能发现哪些等量关系?同学们互相交流,说说理由.在上述操作过程中,你会得出什么结论?在等圆中,相等的圆心角所对的弧相等,所对的弦相等.学生互相讨论交流,看一看命题的证明.讨论:上面的结论,在同圆中也成立吗?思考解题方法,自己试着独立完成
板书设计 圆的对称性一、圆的旋转不变性圆是中心对称图形,对称中心为圆心.二、圆心角、弧、弦之间相等关系定理.证明:略三、随堂练习四、课时小结五、课后作业
迁移拓展训练 1.为什么有些电影院的坐位排列(横排)呈圆弧形?说一说这种设计的合理性.答:有些电影院的坐位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视角相等.
本课最大特色 思考后讨论,再交流,展示解决问题的思想和方案。将实际问题转化为数学问题,从而提高学习数学的兴趣。
教学反思
教师集体备课教案
科目 数学 年级 九年级 主备人 杨道之
课 题 圆的对称性 上课人
知识与技能目标 圆的旋转不变性.圆心角、弧、弦之间相等关系定理.
过程与方法目标 通过观察、比较、操作、推理、归纳等活动,发展空间观念、推理能力以及概括问题的能力.
情感态度与价值观目标 利用圆的旋转不变性,研究圆心角、弧、弦之间相等关系定理.培养学生积极探索数学问题的态度及方法.
教学重点 圆心角、弧、弦之间关系定理
教学难点 “圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明.
问题探讨 圆心角、弧、弦之间有怎样的关系
要点记忆 圆心角、弧、弦之间关系定理
教具、学具准备 圆规,常规教具
教 学 过 程
教 师 活 动 学生活动
一.创设问题情境,引入新课我们研究过中心对称图形,我们是用什么方法来研究它的,它的定义是什么?圆是一个特殊的圆形,通过前面的学习,同学们已经了解到圆既是一个轴对称图形又是一个中心对称图形.那么,圆还有其他特性吗?下面我们继续来探讨.二.讲授新课把这两个圆叠在一起,使它俩重合,将圆心固定.将上面这个圆旋转任意一个角度,两个圆还重合吗?通过旋转的方法我们知道:圆具有旋转不变的特性.即一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.圆的中心对称性是其旋转不变性的特例.即圆是中心对称图形,对称中心为圆心.按下面的步骤做一做:1.在两张透明纸上,作两个半径相等的⊙O和⊙O′,沿圆周分别将两圆剪下.2.在⊙O和⊙O'上分别作相等的圆心角∠AOB和∠A'O'B'(如下图示),圆心固定.注意:在画∠AOB与∠A'O'B'时,要使OB相对于OA的方向与O'B'相对于O'A'的方向一致,否则当OA与OA'重合时,OB与O'B'不能重合.3.将其中的一个圆旋转一个角度,使得OA与O'A'重合.由已知条件可知∠AOB=∠A'O'B'.由两圆的半径相等,可以得到∠OAB=∠OBA=∠O'A'B'=∠O'B'A'.由△AOB≌△A'O'B',可得到AB=A'B'.由旋转法可知.……我们在上述做一做的过程中发现,固定圆心,将其中一个圆旋转一个角度,使半径OA与O'A'重合时,由于∠AOB=∠A'O'B'.这样便得到半径OB与O'B'重合.因为点A和点A'重合,点B和点B'重合,所以和重合,弦AB与弦A'B'重合,即,AB=A'B'.如上图所示,已知:⊙O和⊙O'是两个半径相等的圆,∠AOB=∠A'O'B'.求证:,AB=A'B'.上面的结论,在同圆中也成立.于是得到下面的定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等3、例题讲解如下图,⊙O的直径AB=10cm,C为⊙O上的一点,∠ABC=30°,求AC的长.解:∵AB为⊙O的直径.∴∠ACB=90°.又∵∠ABC=30°,∴AC=AB=×10=5(cm).4.课时小结5.课后作业 思考回答问题:(用旋转的方法.中心对称图形是指把一个图形绕某一个点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫中心对称图形.这个点就是它的对称中心.)观察两个圆有什么特点?动手操作通过上面的做一做,你能发现哪些等量关系?同学们互相交流,说说理由.在上述操作过程中,你会得出什么结论?在等圆中,相等的圆心角所对的弧相等,所对的弦相等.学生互相讨论交流,看一看命题的证明.讨论:上面的结论,在同圆中也成立吗?思考解题方法,自己试着独立完成
板书设计 圆的对称性一、圆的旋转不变性圆是中心对称图形,对称中心为圆心.二、圆心角、弧、弦之间相等关系定理.证明:略三、随堂练习四、课时小结五、课后作业
迁移拓展训练 1.为什么有些电影院的坐位排列(横排)呈圆弧形?说一说这种设计的合理性.答:有些电影院的坐位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视角相等.
本课最大特色 思考后讨论,再交流,展示解决问题的思想和方案。将实际问题转化为数学问题,从而提高学习数学的兴趣。
教学反思
