五年级上学期数学6.5整理和复习课件(共22张PPT)人教版
文档属性
| 名称 | 五年级上学期数学6.5整理和复习课件(共22张PPT)人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 744.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 07:13:16 | ||
图片预览




文档简介
(共22张PPT)
组合和复习
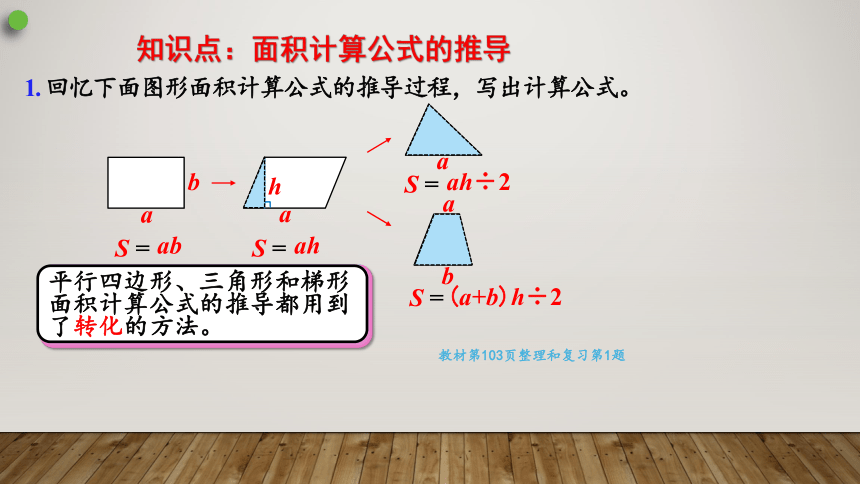
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
知识点:面积计算公式的推导
教材第103页整理和复习第1题
平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。
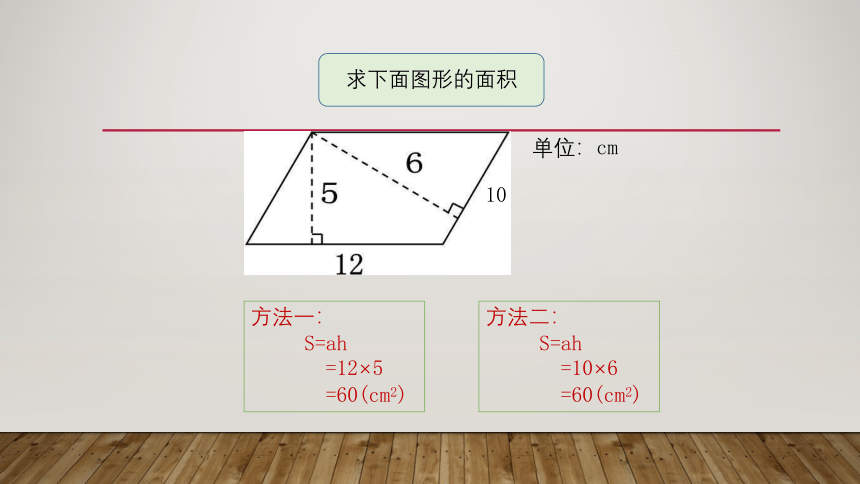
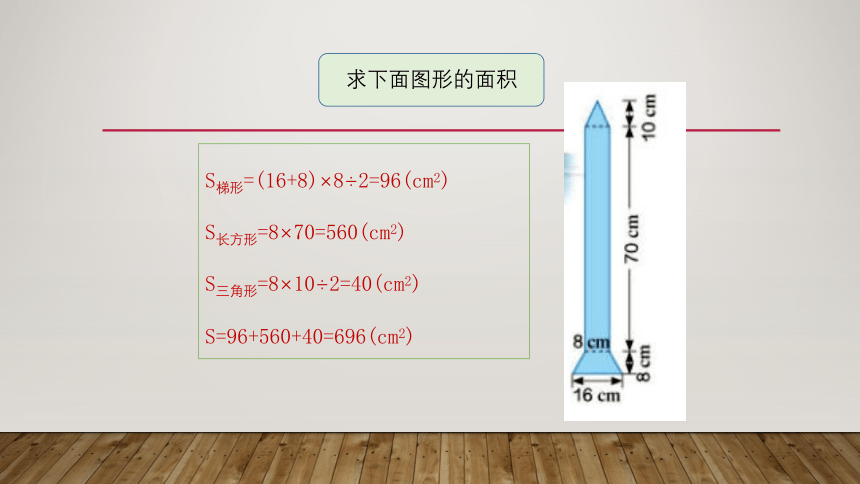
求下面图形的面积
10
单位:cm
方法一:
S=ah
=12×5
=60(cm2)
方法二:
S=ah
=10×6
=60(cm2)
要注意什么?
要注意解方程的书写格式。
S=ah÷2
=3.41(m2)
=2.2×3.1÷2
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(36+14)×21÷2
=50×21÷2
计算平行四边形、三角形时,还得注意底和高要相对应。
上底
下 底
高
上底
下 底
高
上底
下 底
高
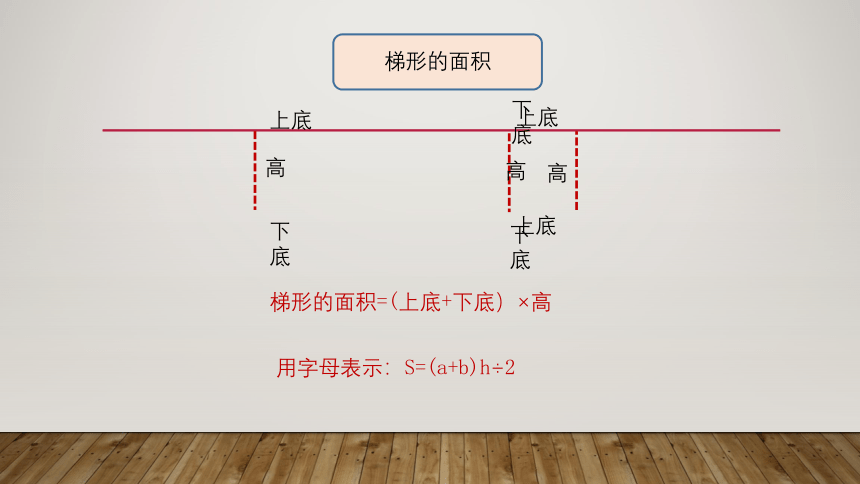
梯形的面积=(上底+下底)×高
梯形的面积
用字母表示:S=(a+b)h÷2
用字母表示数
用字母表示数
1.用字母表示一个数。
2.用字母表示变化的数及数量关系。
3.用字母表示运算律。
知识点:图形间的关系
图形间的面积比较,往往牵涉到图形间的关系:
1.三角形的面积是与它等底等高的平行四边形面积的一半。
2.等底等高的平行四边形面积相等;
3.等底等高的三角形面积相等;
4.面积相等的平行四边形、三角形或梯形,形状不一定相同。
求下面图形的面积
S梯形=(16+8)×8÷2=96(cm2)
S长方形=8×70=560(cm2)
S三角形=8×10÷2=40(cm2)
S=96+560+40=696(cm2)
方程的解法
方程的解
解方程
使方程左右两边相等的未知数的值,叫做方程的解。
形如ax=b的方程 解:ax÷a=b÷a x=b÷a
形如a-x=b的方程 解:a-x+x=b+x b+x=a x=a-b
形如ax±b=c的方程把ax看成一个整体
形如a(x±b)=c的方程把(x±b)看成一个整体
方程的解法
S三角形=10×(12 6)÷2
=30(cm2)
S梯形=(6+12)×5÷2
=45(cm2)
S=30+45=75(cm2)
知识点:组合图形的面积计算
分割成三角形和梯形
方法三
计算下面图形的面积。你能想出几种方法?
解下列方程。
x÷8=0.4 6x+18=48
解:x÷8×8=0.4×8
x=3.2
解:6x+18-18=48-18
6x=30
6x÷6=30÷6
x=5
等式的性质2
等式的性质1、2
填 空
1、一个平行四边形的面积是150平方分米,和它等底等高的三角形的面积是( )平方分米。
2、一个直角梯形的下底是8厘米,如果把上底增加3厘米,它就变成了一个正方形。这个梯形的面积是( )。
75平方分米
52平方厘米
知识点:不规则图形面积的估算
S三角形=ah÷2
=10×8÷2
=40(cm2)
答:阴影部分的面积约是40 cm2。
转化成三角形
方法二
图中每个小方格的面积是1 cm ,阴影部分的面积约是多少平方厘米?
高=15÷3=5(米)
面积=15×5÷2=37.5(平方米)
答:这个花坛的占地面积是37.5 平方米。
我 会 做
一个三角形的花坛,底边长15米,是高的3倍。求这个花坛的占地面积是多少
解法一
解:设他两个月前的体重是x kg。
两个月前的体重-3=现在的体重
x-3=93
答:他两个月前的体重是96 kg。
x-3+3=93+3
x=96
有一台收割机,作业宽度是1.8 m。每小时行5 km,大约多少小时可以收割完下边这块地?
200 m
330 m
100 m
先求这块地的面积,然后计算出收割机的工作效率,最后算工作时间。
5 km = 5000 m
1.8×5000 = 9000(m2)
(200+330)×100÷2 = 26500(m2)
26500÷9000 ≈ 3(时)
答:大约3小时可以收割完这块地。
教材第104页第4题
我 会 做
有一个花坛长35米,宽24米。如果在花坛四周修一条2.5米宽的小路,小路的面积是多少
(35+2.5+2.5)×(24+2.5+2.5)
-35×24
=320(平方米)
答:小路的面积是320 平方米。
35
24
2.5
5×路灯的盏数=灯泡的总数
解:设一共有x盏路灯。
5×路灯的盏数=灯泡的总数
5x=140
答:一共有28盏路灯。
5x÷5=140÷5
x=28
图中小方格的边长是1 m,请你估计涂色部分的面积。
=26+42÷2
=47(m2)
=26+21
答:涂色部分的面积大约是47m2 。
本题可采用数方格的方法进行估计。
S=S全格+S半格
教材第105页第8*题
Goodbye~
感谢聆听,下期再会
组合和复习
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
知识点:面积计算公式的推导
教材第103页整理和复习第1题
平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。
求下面图形的面积
10
单位:cm
方法一:
S=ah
=12×5
=60(cm2)
方法二:
S=ah
=10×6
=60(cm2)
要注意什么?
要注意解方程的书写格式。
S=ah÷2
=3.41(m2)
=2.2×3.1÷2
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(36+14)×21÷2
=50×21÷2
计算平行四边形、三角形时,还得注意底和高要相对应。
上底
下 底
高
上底
下 底
高
上底
下 底
高
梯形的面积=(上底+下底)×高
梯形的面积
用字母表示:S=(a+b)h÷2
用字母表示数
用字母表示数
1.用字母表示一个数。
2.用字母表示变化的数及数量关系。
3.用字母表示运算律。
知识点:图形间的关系
图形间的面积比较,往往牵涉到图形间的关系:
1.三角形的面积是与它等底等高的平行四边形面积的一半。
2.等底等高的平行四边形面积相等;
3.等底等高的三角形面积相等;
4.面积相等的平行四边形、三角形或梯形,形状不一定相同。
求下面图形的面积
S梯形=(16+8)×8÷2=96(cm2)
S长方形=8×70=560(cm2)
S三角形=8×10÷2=40(cm2)
S=96+560+40=696(cm2)
方程的解法
方程的解
解方程
使方程左右两边相等的未知数的值,叫做方程的解。
形如ax=b的方程 解:ax÷a=b÷a x=b÷a
形如a-x=b的方程 解:a-x+x=b+x b+x=a x=a-b
形如ax±b=c的方程把ax看成一个整体
形如a(x±b)=c的方程把(x±b)看成一个整体
方程的解法
S三角形=10×(12 6)÷2
=30(cm2)
S梯形=(6+12)×5÷2
=45(cm2)
S=30+45=75(cm2)
知识点:组合图形的面积计算
分割成三角形和梯形
方法三
计算下面图形的面积。你能想出几种方法?
解下列方程。
x÷8=0.4 6x+18=48
解:x÷8×8=0.4×8
x=3.2
解:6x+18-18=48-18
6x=30
6x÷6=30÷6
x=5
等式的性质2
等式的性质1、2
填 空
1、一个平行四边形的面积是150平方分米,和它等底等高的三角形的面积是( )平方分米。
2、一个直角梯形的下底是8厘米,如果把上底增加3厘米,它就变成了一个正方形。这个梯形的面积是( )。
75平方分米
52平方厘米
知识点:不规则图形面积的估算
S三角形=ah÷2
=10×8÷2
=40(cm2)
答:阴影部分的面积约是40 cm2。
转化成三角形
方法二
图中每个小方格的面积是1 cm ,阴影部分的面积约是多少平方厘米?
高=15÷3=5(米)
面积=15×5÷2=37.5(平方米)
答:这个花坛的占地面积是37.5 平方米。
我 会 做
一个三角形的花坛,底边长15米,是高的3倍。求这个花坛的占地面积是多少
解法一
解:设他两个月前的体重是x kg。
两个月前的体重-3=现在的体重
x-3=93
答:他两个月前的体重是96 kg。
x-3+3=93+3
x=96
有一台收割机,作业宽度是1.8 m。每小时行5 km,大约多少小时可以收割完下边这块地?
200 m
330 m
100 m
先求这块地的面积,然后计算出收割机的工作效率,最后算工作时间。
5 km = 5000 m
1.8×5000 = 9000(m2)
(200+330)×100÷2 = 26500(m2)
26500÷9000 ≈ 3(时)
答:大约3小时可以收割完这块地。
教材第104页第4题
我 会 做
有一个花坛长35米,宽24米。如果在花坛四周修一条2.5米宽的小路,小路的面积是多少
(35+2.5+2.5)×(24+2.5+2.5)
-35×24
=320(平方米)
答:小路的面积是320 平方米。
35
24
2.5
5×路灯的盏数=灯泡的总数
解:设一共有x盏路灯。
5×路灯的盏数=灯泡的总数
5x=140
答:一共有28盏路灯。
5x÷5=140÷5
x=28
图中小方格的边长是1 m,请你估计涂色部分的面积。
=26+42÷2
=47(m2)
=26+21
答:涂色部分的面积大约是47m2 。
本题可采用数方格的方法进行估计。
S=S全格+S半格
教材第105页第8*题
Goodbye~
感谢聆听,下期再会
