人教版(B版2019课标)高中数学必修四11.4.1直线与平面垂直 学案(无答案)
文档属性
| 名称 | 人教版(B版2019课标)高中数学必修四11.4.1直线与平面垂直 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 102.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 00:00:00 | ||
图片预览

文档简介
直线与平面垂直
【学习目标】
1.通过直线与平面垂直的定义学习,培养直观想象的数学核心素养。
2.借助线面垂直的性质定理与判定定理,提升逻辑推理、数学抽象的数学核心素养。
【学习重难点】
1.了解直线与平面垂直的定义。
2.掌握线面垂直的性质定理,并能应用。
3.理解直线与平面垂直的判定定理,并会用其判断直线与平面垂直。
4.灵活运用直线与平面垂直的判定定理和性质定理处理空间垂直问题。
【学习过程】
一、合作探究
1.线面垂直的定义及判定定理的理解
【例1】 下列说法中正确的个数是( )
①如果直线l与平面α内的两条相交直线都垂直,则l⊥α;
②如果直线l与平面α内的任意一条直线垂直,则l⊥α;
③如果直线l不垂直于α,则α内没有与l垂直的直线;
④如果直线l不垂直于α,则α内也可以有无数条直线与l垂直。
A.0 B.1 C.2 D.3
2.线面垂直性质定理的应用
[探究问题]
将一块三角形纸片ABC沿折痕AD折起,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触)。观察折痕AD与桌面的位置关系。
(1)折痕AD与桌面一定垂直吗?
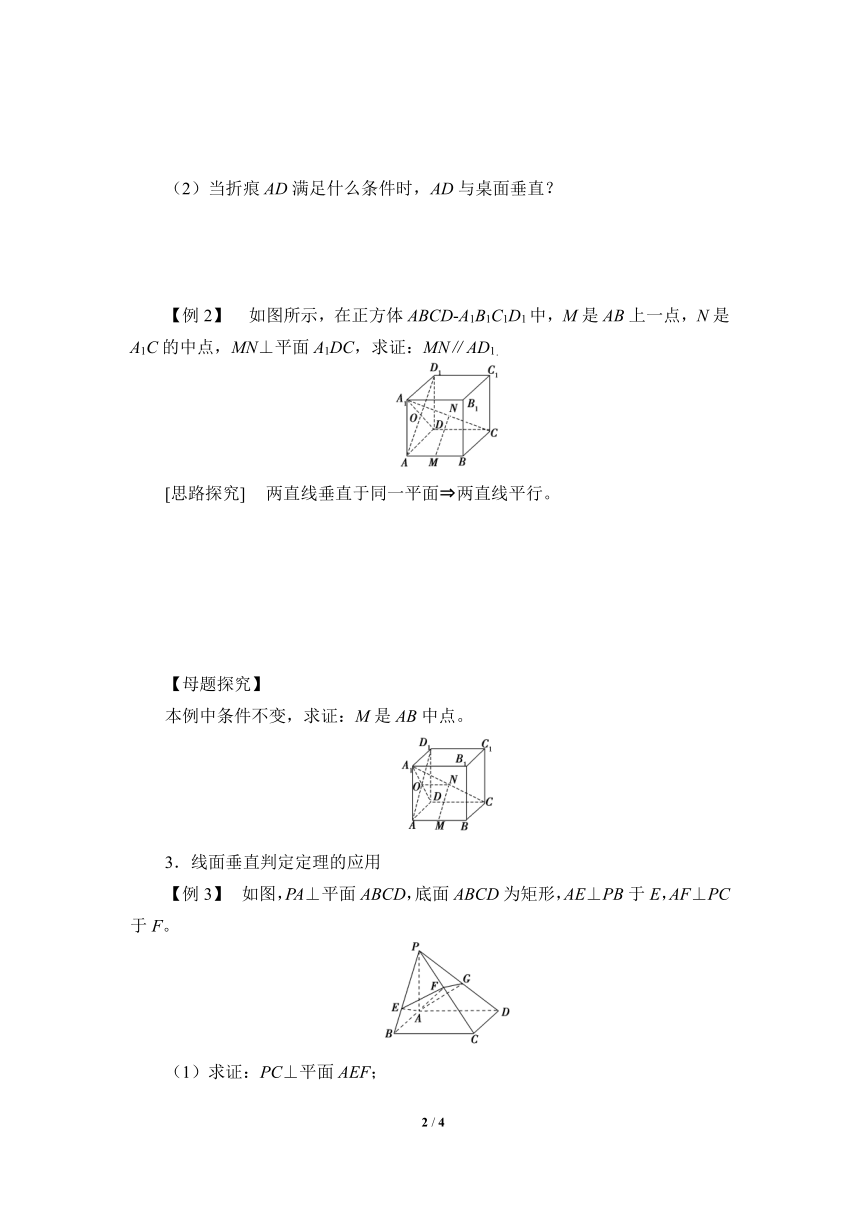
(2)当折痕AD满足什么条件时,AD与桌面垂直?
【例2】 如图所示,在正方体ABCD A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证:MN∥AD1.
[思路探究] 两直线垂直于同一平面 两直线平行。
【母题探究】
本例中条件不变,求证:M是AB中点。
3.线面垂直判定定理的应用
【例3】 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F。
(1)求证:PC⊥平面AEF;
(2)设平面AEF交PD于G,求证:AG⊥PD.
[思路探究] PA⊥平面ABCD,ABCD为矩形,AE⊥PB,AF⊥PC 直线与平面垂直的判定定理;若一条直线垂直于一个平面,则垂直于这个平面内的所有直线。
【学习小结】
1.直线与平面垂直的定义
文字语言 图形语言 符号语言
如果直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直,直线l叫做平面α的垂线,平面α叫做直线l的垂面,它们唯一的公共点P叫做垂足 l⊥α
2.直线与平面垂直的性质定理
文字语言 垂直于同一个平面的两条直线平行
符号语言 a∥b
图形语言
文字语言 两条平行直线中有一条垂直于一个平面,另一条也垂直于这个平面
符号语言 b⊥α
3.直线与平面垂直的判定定理
文字语言 图形语言 符号语言
如果一条直线与平面内的两条相交直线都垂直,则这条直线与这个平面垂直 l⊥α
【精炼反馈】
1.判断(正确的打“√”,错误的打“×”)
(1)垂直于同一条直线的两个平面互相平行。 ( )
(2)垂直于同一平面的两条直线互相平行。 ( )
(3)一条直线在平面内,另一条直线与这个平面垂直,则这两条直线互相垂直。 ( )
2.在圆柱的一个底面上任取一点(该点不在底面圆周上),过该点作另一个底面的垂线,则这条垂线与圆柱的母线所在直线的位置关系是( )
A.相交 B.平行
C.异面 D.相交或平行
3.如图,如果MC⊥菱形ABCD所在平面,那么MA与BD的位置关系是( )
A.平行 B.垂直相交
C.垂直但不相交 D.相交但不垂直
4.如图所示,在四棱锥P ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2,E,F分别是AD,PC的中点。证明:PC⊥平面BEF。
4 / 4
【学习目标】
1.通过直线与平面垂直的定义学习,培养直观想象的数学核心素养。
2.借助线面垂直的性质定理与判定定理,提升逻辑推理、数学抽象的数学核心素养。
【学习重难点】
1.了解直线与平面垂直的定义。
2.掌握线面垂直的性质定理,并能应用。
3.理解直线与平面垂直的判定定理,并会用其判断直线与平面垂直。
4.灵活运用直线与平面垂直的判定定理和性质定理处理空间垂直问题。
【学习过程】
一、合作探究
1.线面垂直的定义及判定定理的理解
【例1】 下列说法中正确的个数是( )
①如果直线l与平面α内的两条相交直线都垂直,则l⊥α;
②如果直线l与平面α内的任意一条直线垂直,则l⊥α;
③如果直线l不垂直于α,则α内没有与l垂直的直线;
④如果直线l不垂直于α,则α内也可以有无数条直线与l垂直。
A.0 B.1 C.2 D.3
2.线面垂直性质定理的应用
[探究问题]
将一块三角形纸片ABC沿折痕AD折起,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触)。观察折痕AD与桌面的位置关系。
(1)折痕AD与桌面一定垂直吗?
(2)当折痕AD满足什么条件时,AD与桌面垂直?
【例2】 如图所示,在正方体ABCD A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证:MN∥AD1.
[思路探究] 两直线垂直于同一平面 两直线平行。
【母题探究】
本例中条件不变,求证:M是AB中点。
3.线面垂直判定定理的应用
【例3】 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F。
(1)求证:PC⊥平面AEF;
(2)设平面AEF交PD于G,求证:AG⊥PD.
[思路探究] PA⊥平面ABCD,ABCD为矩形,AE⊥PB,AF⊥PC 直线与平面垂直的判定定理;若一条直线垂直于一个平面,则垂直于这个平面内的所有直线。
【学习小结】
1.直线与平面垂直的定义
文字语言 图形语言 符号语言
如果直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直,直线l叫做平面α的垂线,平面α叫做直线l的垂面,它们唯一的公共点P叫做垂足 l⊥α
2.直线与平面垂直的性质定理
文字语言 垂直于同一个平面的两条直线平行
符号语言 a∥b
图形语言
文字语言 两条平行直线中有一条垂直于一个平面,另一条也垂直于这个平面
符号语言 b⊥α
3.直线与平面垂直的判定定理
文字语言 图形语言 符号语言
如果一条直线与平面内的两条相交直线都垂直,则这条直线与这个平面垂直 l⊥α
【精炼反馈】
1.判断(正确的打“√”,错误的打“×”)
(1)垂直于同一条直线的两个平面互相平行。 ( )
(2)垂直于同一平面的两条直线互相平行。 ( )
(3)一条直线在平面内,另一条直线与这个平面垂直,则这两条直线互相垂直。 ( )
2.在圆柱的一个底面上任取一点(该点不在底面圆周上),过该点作另一个底面的垂线,则这条垂线与圆柱的母线所在直线的位置关系是( )
A.相交 B.平行
C.异面 D.相交或平行
3.如图,如果MC⊥菱形ABCD所在平面,那么MA与BD的位置关系是( )
A.平行 B.垂直相交
C.垂直但不相交 D.相交但不垂直
4.如图所示,在四棱锥P ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2,E,F分别是AD,PC的中点。证明:PC⊥平面BEF。
4 / 4
