沪科版数学八年级下册 17.5 一元二次方程的应用-课件(共15张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 17.5 一元二次方程的应用-课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 11:11:27 | ||
图片预览



文档简介
(共15张PPT)
17.5 一元二次方程的应用
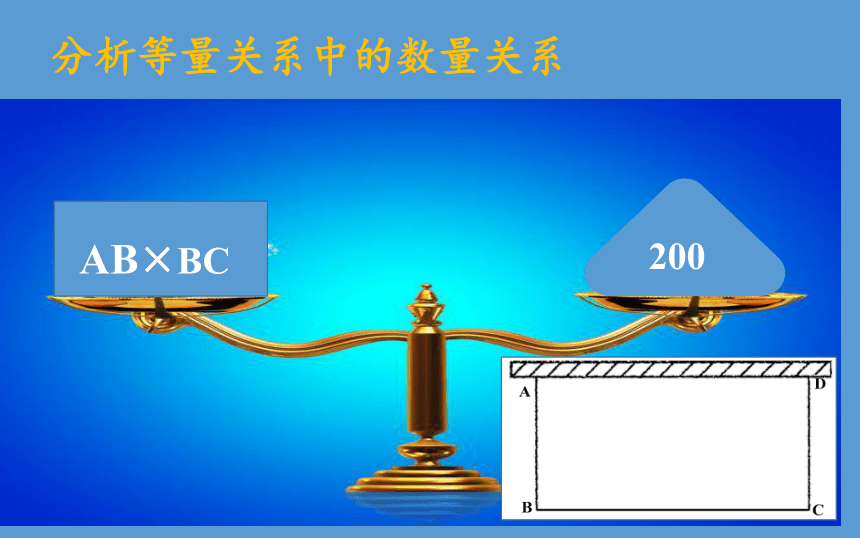
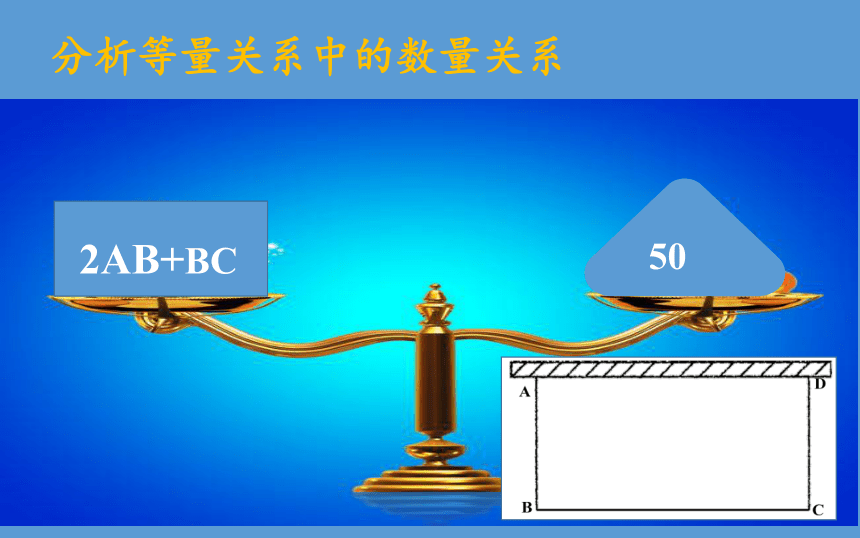
如图,为建设美丽校园,学校采纳了广大师生的意见,准备利用一面围墙和旁边的空地,建一个面积为200m2的长方形花圃,另三边用木质围栏围成,若木栏总长50m,围墙足够长,你能帮助学校设计出这个花圃吗?
问 题
如何解决这个实际问题?
数学问题
转化
方程
分析等量关系中的数量关系
200
AB×BC
分析等量关系中的数量关系
50
2AB+BC
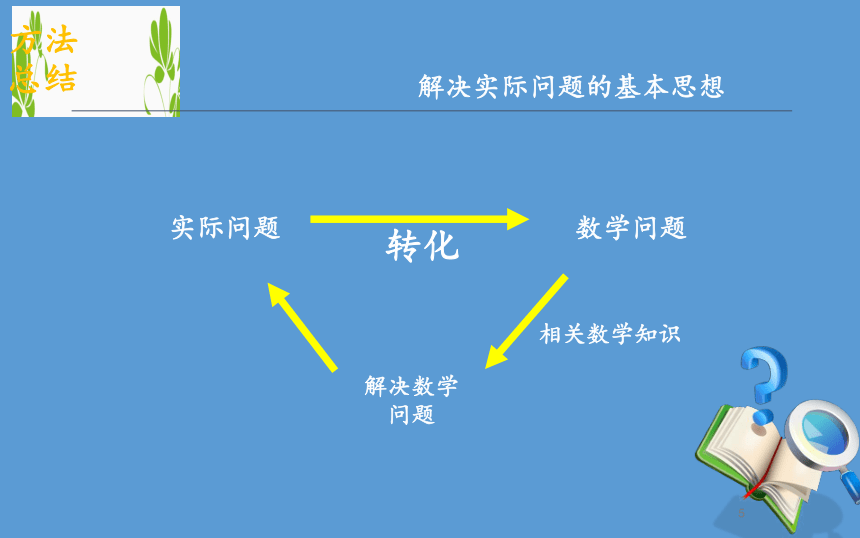
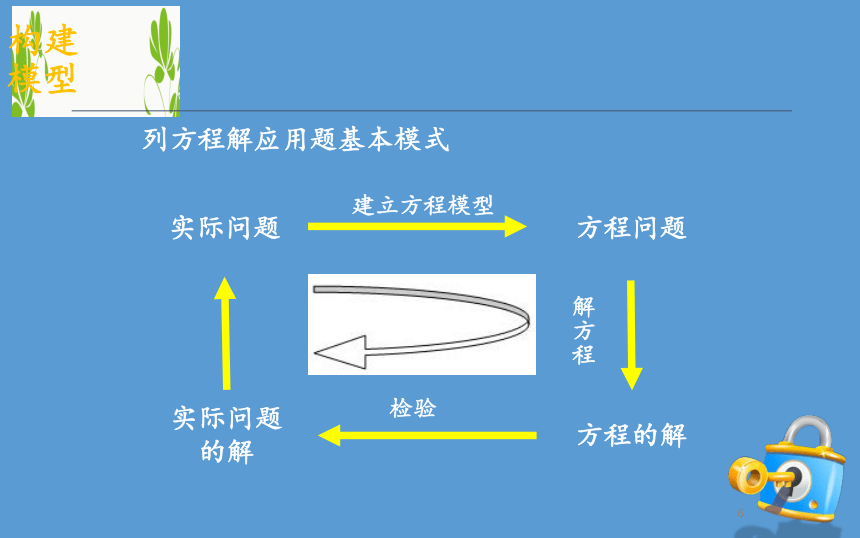
方法总结解决实际问题的基本思想实际问题数学问题解决数学问题转化相关数学知识构建模型列方程解应用题基本模式实际问题方程问题实际问题的解方程的解建立方程模型解方程检验 某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?
模型应用
81
若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
1+
1轮新感染数
2轮新感染数
+
与平均感染数有关
与1轮后总感染数有关
也与平均感染数有关
抓住模型 以不变应万变
大江东去浪淘尽,千古风流数人物; 而立之年督东吴,早逝英年两位数; 十位恰小个位三,个位平方与寿符;哪位同学算得快,多少年华属周瑜?
早逝英年两位数
个位平方
与十位和个位数字有关
十位与个位数字有关
与个位数字有关
模型总结
列方程解应用题的模型中
关键是:
等量关系
难点是:
分析等量关系中的量以及量与量之间的关系
模型总结
列方程解应用题的模型步骤
1、等量关系
2、分析等量关系中各数量之间的关系
3、选择合适的设法(完整)
4、列出方程
5、解方程
6、检验根
7、答(完整)
作 业
课本45页习题17.5 2、3、4、5、6
感谢您的聆听!
若每件工艺品按150元进货,200元标价售出,工艺商场每天可售出该工艺品120件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天可获得4800元的利润
4800
每件利润×销量
抓住模型 以不变应万变
4800
每件利润×销量
与降价有关
与降价有关
分析它们之间的数量关系
抓住模型 以不变应万变
若每件工艺品按150元进货,200元标价售出,工艺商场每天可售出该工艺品120件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天可获得4800元的利润
谢 谢
17.5 一元二次方程的应用
如图,为建设美丽校园,学校采纳了广大师生的意见,准备利用一面围墙和旁边的空地,建一个面积为200m2的长方形花圃,另三边用木质围栏围成,若木栏总长50m,围墙足够长,你能帮助学校设计出这个花圃吗?
问 题
如何解决这个实际问题?
数学问题
转化
方程
分析等量关系中的数量关系
200
AB×BC
分析等量关系中的数量关系
50
2AB+BC
方法总结解决实际问题的基本思想实际问题数学问题解决数学问题转化相关数学知识构建模型列方程解应用题基本模式实际问题方程问题实际问题的解方程的解建立方程模型解方程检验 某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?
模型应用
81
若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
1+
1轮新感染数
2轮新感染数
+
与平均感染数有关
与1轮后总感染数有关
也与平均感染数有关
抓住模型 以不变应万变
大江东去浪淘尽,千古风流数人物; 而立之年督东吴,早逝英年两位数; 十位恰小个位三,个位平方与寿符;哪位同学算得快,多少年华属周瑜?
早逝英年两位数
个位平方
与十位和个位数字有关
十位与个位数字有关
与个位数字有关
模型总结
列方程解应用题的模型中
关键是:
等量关系
难点是:
分析等量关系中的量以及量与量之间的关系
模型总结
列方程解应用题的模型步骤
1、等量关系
2、分析等量关系中各数量之间的关系
3、选择合适的设法(完整)
4、列出方程
5、解方程
6、检验根
7、答(完整)
作 业
课本45页习题17.5 2、3、4、5、6
感谢您的聆听!
若每件工艺品按150元进货,200元标价售出,工艺商场每天可售出该工艺品120件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天可获得4800元的利润
4800
每件利润×销量
抓住模型 以不变应万变
4800
每件利润×销量
与降价有关
与降价有关
分析它们之间的数量关系
抓住模型 以不变应万变
若每件工艺品按150元进货,200元标价售出,工艺商场每天可售出该工艺品120件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天可获得4800元的利润
谢 谢
