沪科版数学八年级下册 17.1 一元二次方程教案
文档属性
| 名称 | 沪科版数学八年级下册 17.1 一元二次方程教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 303.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 00:00:00 | ||
图片预览

文档简介
《17.1 一元二次方程》教案
学习目标:
1、会根据具体问题列出一元二次方程,体会方程的模型思想,提高归纳、分析的能力.
2、理解一元二次方程的概念;知道一元二次方程的一般形式;会把一个一元二次方程化为一般形式;会判断一元二次方程的二次项系数、一次项系数和常数项.
重点:
由实际问题列出一元二次方程和一元二次方程的概念.
难点:
由实际问题列出一元二次方程.准确认识一元二次方程的二次项和系数以及一次项和系数还有常数项.
教学过程:
一、复习导入
1、什么是一元一次方程?
有一个未知数,未知数的最高次数是一的整式方程叫做一元一次方程
2、一元一次方程的一般形式是什么?
ax+b=0
二、探索新知
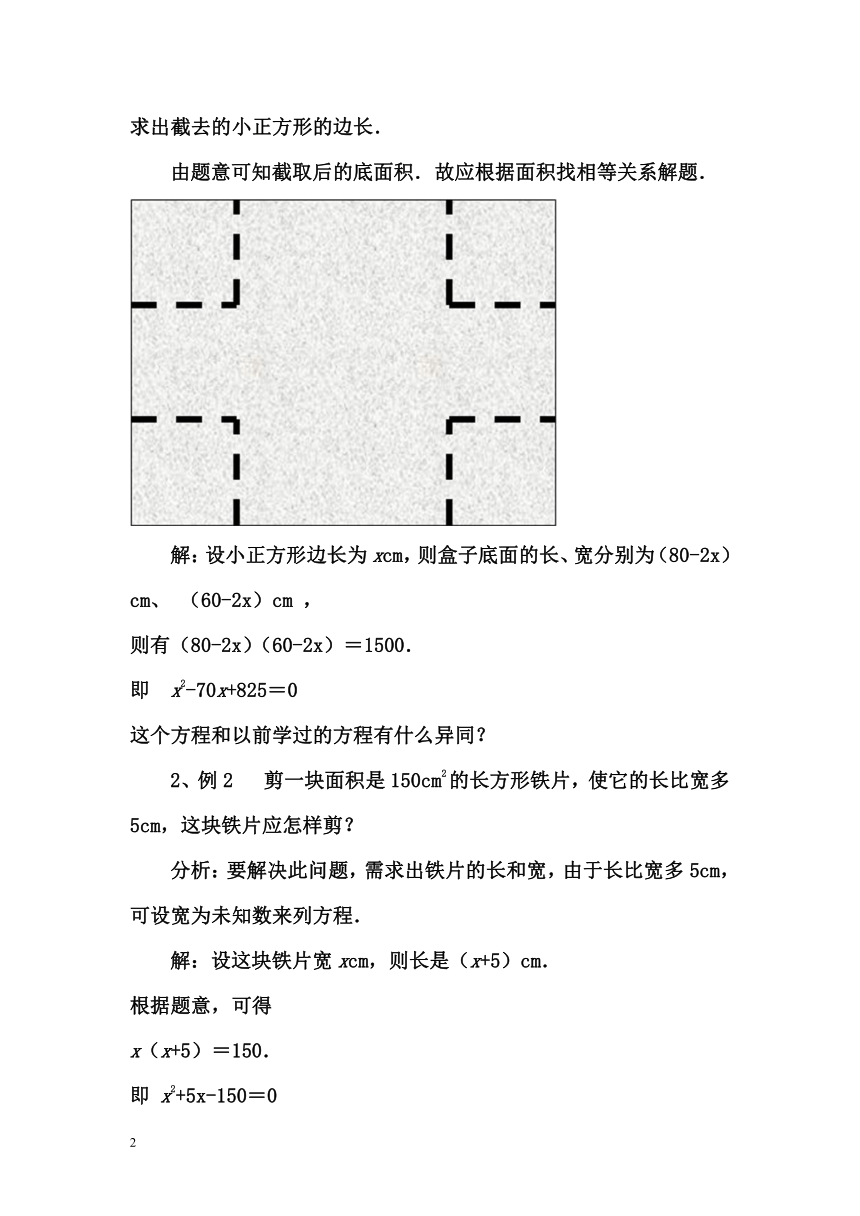
1、例1 用一块长80cm,宽60cm的薄钢片,在四个角上截去四个相同的小正方形,然后做成底面积为1500cm2的无盖长方形盒子.试求出截去的小正方形的边长.
由题意可知截取后的底面积.故应根据面积找相等关系解题.
解:设小正方形边长为xcm,则盒子底面的长、宽分别为(80-2x)cm、 (60-2x)cm ,
则有(80-2x)(60-2x)=1500.
即 x2-70x+825=0
这个方程和以前学过的方程有什么异同?
2、例2 剪一块面积是150cm2的长方形铁片,使它的长比宽多5cm,这块铁片应怎样剪?
分析:要解决此问题,需求出铁片的长和宽,由于长比宽多5cm,可设宽为未知数来列方程.
解:设这块铁片宽xcm,则长是(x+5)cm.
根据题意,可得
x(x+5)=150.
即 x2+5x-150=0
3、例3 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应该邀请多少个队参赛?
解:设应邀请x个队参加比赛,由题意得:
0.5x(x-1)=28
4、观察这两个方程有什么共同点?
x2-70x+825=0
x2+5x-150=0
方程中未知数的个数、次数各是多少?
5、总结:
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2 (二次)的方程,叫做一元二次方程.
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:
ax2+bx+c=0 (a≠0)
这种形式叫做一元二次方程的一般形式,其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
三、小试牛刀
1、在下列方程中,是一元二次方程是( )
A.x2+5x-150=0 B. ax2+bx+c=0
C. (x-2)(x+5)=x2 D. x2+5x-150=5-x2
2、方程2x2=3(x-6)化为一般形式后,二次项系数、一次项系数、常数项分别是( )
3、p x2-3x+p2-q=0是关于x的一元二次方程,则( )
A.p=1 B.p>0 C .p≠0 D.p为任意实数
4、关于x的方程( a-1)x2+3x=0是一元二次方程,则a的取值范围是( )
四、自主探究:
1、大江东去浪淘尽,数千古风流人物,而立之年督东吴,早逝英年两位数,十位恰小个位三,个位平方与寿符,哪位学子算得快,多少年华属周瑜?要想知道这位英年早逝的东吴都督的年龄,我们该怎么来思考这个问题呢?
解 设周瑜逝世时的年龄个位数为x, 则十位数字为(x-3)
根据题意得方程:
x2=10(x-3)+x,
整理得:
x2-11x+30=0.
五、我能行!
2、某蔬菜队2009年全年无公害蔬菜产量为100t,计划2011年无公害蔬菜要比2009年翻一番(即为200t),要实现这个目标,2010年和2011年无公害蔬菜的年平均增长率是多少?
解 设年平均增长率为x,则2010年的产量为100(1+x),
2011年产量为100(1+x)2 ,
100(1+x)2=200
整理得:x2+2x-1=0
六、小结
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax2+bx+c=0 (a≠0)这种形式叫做一元二次方程的一般形式,其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
七、自我归纳:
1、本节课我们学习了哪些知识?
2、学习过程中用了哪些数学方法?
3、确定一元二次方程的项及系数时要注意什么?
八、作业:
1、阅读课文19-20页
2、第21页练习:1.2.3.4题
3、第21页习题17.1:1.2.3题
5
学习目标:
1、会根据具体问题列出一元二次方程,体会方程的模型思想,提高归纳、分析的能力.
2、理解一元二次方程的概念;知道一元二次方程的一般形式;会把一个一元二次方程化为一般形式;会判断一元二次方程的二次项系数、一次项系数和常数项.
重点:
由实际问题列出一元二次方程和一元二次方程的概念.
难点:
由实际问题列出一元二次方程.准确认识一元二次方程的二次项和系数以及一次项和系数还有常数项.
教学过程:
一、复习导入
1、什么是一元一次方程?
有一个未知数,未知数的最高次数是一的整式方程叫做一元一次方程
2、一元一次方程的一般形式是什么?
ax+b=0
二、探索新知
1、例1 用一块长80cm,宽60cm的薄钢片,在四个角上截去四个相同的小正方形,然后做成底面积为1500cm2的无盖长方形盒子.试求出截去的小正方形的边长.
由题意可知截取后的底面积.故应根据面积找相等关系解题.
解:设小正方形边长为xcm,则盒子底面的长、宽分别为(80-2x)cm、 (60-2x)cm ,
则有(80-2x)(60-2x)=1500.
即 x2-70x+825=0
这个方程和以前学过的方程有什么异同?
2、例2 剪一块面积是150cm2的长方形铁片,使它的长比宽多5cm,这块铁片应怎样剪?
分析:要解决此问题,需求出铁片的长和宽,由于长比宽多5cm,可设宽为未知数来列方程.
解:设这块铁片宽xcm,则长是(x+5)cm.
根据题意,可得
x(x+5)=150.
即 x2+5x-150=0
3、例3 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应该邀请多少个队参赛?
解:设应邀请x个队参加比赛,由题意得:
0.5x(x-1)=28
4、观察这两个方程有什么共同点?
x2-70x+825=0
x2+5x-150=0
方程中未知数的个数、次数各是多少?
5、总结:
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2 (二次)的方程,叫做一元二次方程.
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:
ax2+bx+c=0 (a≠0)
这种形式叫做一元二次方程的一般形式,其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
三、小试牛刀
1、在下列方程中,是一元二次方程是( )
A.x2+5x-150=0 B. ax2+bx+c=0
C. (x-2)(x+5)=x2 D. x2+5x-150=5-x2
2、方程2x2=3(x-6)化为一般形式后,二次项系数、一次项系数、常数项分别是( )
3、p x2-3x+p2-q=0是关于x的一元二次方程,则( )
A.p=1 B.p>0 C .p≠0 D.p为任意实数
4、关于x的方程( a-1)x2+3x=0是一元二次方程,则a的取值范围是( )
四、自主探究:
1、大江东去浪淘尽,数千古风流人物,而立之年督东吴,早逝英年两位数,十位恰小个位三,个位平方与寿符,哪位学子算得快,多少年华属周瑜?要想知道这位英年早逝的东吴都督的年龄,我们该怎么来思考这个问题呢?
解 设周瑜逝世时的年龄个位数为x, 则十位数字为(x-3)
根据题意得方程:
x2=10(x-3)+x,
整理得:
x2-11x+30=0.
五、我能行!
2、某蔬菜队2009年全年无公害蔬菜产量为100t,计划2011年无公害蔬菜要比2009年翻一番(即为200t),要实现这个目标,2010年和2011年无公害蔬菜的年平均增长率是多少?
解 设年平均增长率为x,则2010年的产量为100(1+x),
2011年产量为100(1+x)2 ,
100(1+x)2=200
整理得:x2+2x-1=0
六、小结
一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式:ax2+bx+c=0 (a≠0)这种形式叫做一元二次方程的一般形式,其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
七、自我归纳:
1、本节课我们学习了哪些知识?
2、学习过程中用了哪些数学方法?
3、确定一元二次方程的项及系数时要注意什么?
八、作业:
1、阅读课文19-20页
2、第21页练习:1.2.3.4题
3、第21页习题17.1:1.2.3题
5
