8.5.3平面与平面平行的性质 课件(共27张PPT)
文档属性
| 名称 | 8.5.3平面与平面平行的性质 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 13:53:37 | ||
图片预览





文档简介
(共27张PPT)
平面与平面平行的性质
【目标认知】
课程标准 学业要求
从平面与平面平行的定义和基本事实出发,借助长方体,通过直观感知,了解空间中平面与平面的平行关系,归纳出平面与平面平行的性质定理,并加以证明 1.通过直观感知、操作确认,能够归纳出平面与平面平行的性质定理,并能够证明.
2.能够运用性质定理证明一些空间位置关系的简单命题
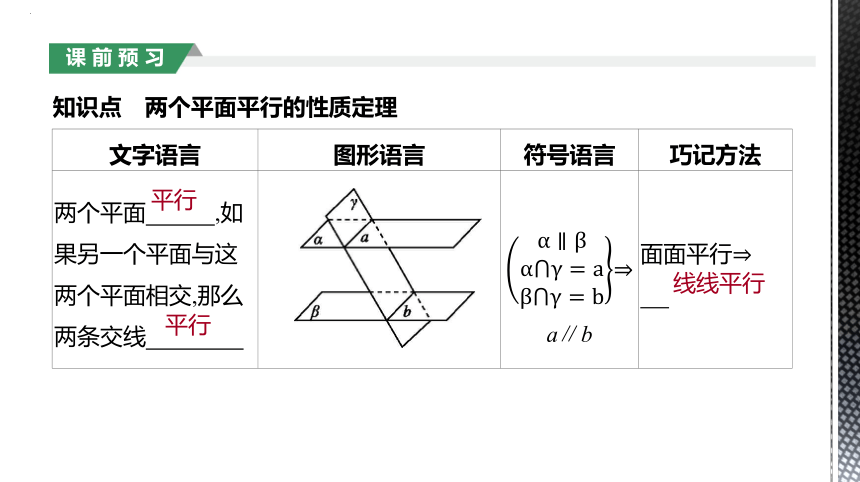
文字语言 图形语言 符号语言 巧记方法
两个平面 ,如果另一个平面与这两个平面相交,那么两条交线 a∥b 面面平行
知识点 两个平面平行的性质定理
平行
平行
课 前 预 习
线线平行
【诊断分析】 1.判断下列说法的正误.(正确的打“√”,错误的打“×”)
(1)如果两个平面分别平行于第三个平面,那么这两个平面平行. ( )
(2)若两个平面平行,则两个平面内的所有直线都相互平行. ( )
(3)若两个平面平行,则其中一个平面内的直线必平行于另一个平面. ( )
√
课 前 预 习
×
[解析]因为两个平面平行,所以分别在两个平面内的两条直线无公共点,它们平行或异面.
√
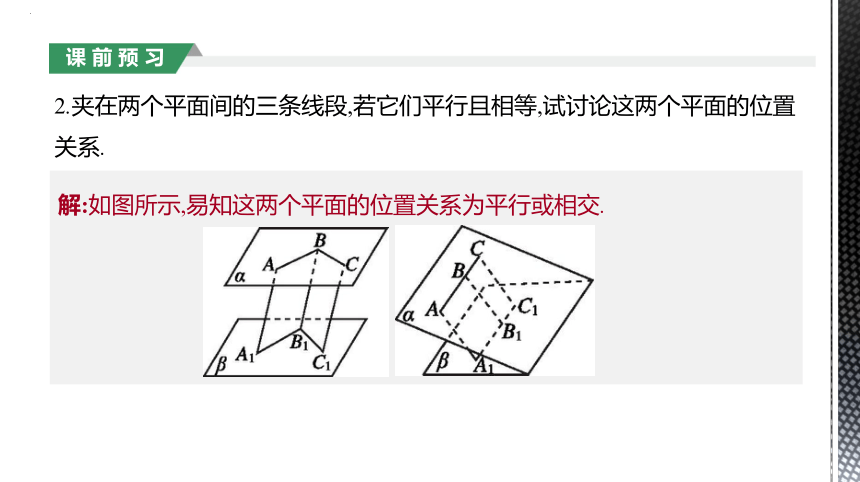
2.夹在两个平面间的三条线段,若它们平行且相等,试讨论这两个平面的位置关系.
课 前 预 习
解:如图所示,易知这两个平面的位置关系为平行或相交.
平面与平面平行的性质定理解读
(1)平面与平面平行的性质定理可简述为“若面面平行,则线线平行”.
(2)夹在两个平行平面间的平行线段长度相等.
(3)经过平面外一点,有且仅有一个平面和已知平面平行.
(4)若两个平面平行于第三个平面,则这两个平面互相平行.
备 课 素 材
探究点一 面面平行的性质定理的应用
例1 如图8-5-28所示,四边形ABCD所在的平面与平面α平行,且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形.求证:四边形ABCD是平行四边形.(注:平行投影的投影线互相平行)
课 中 探 究
证明:因为平面ABCD∥平面α,平面ABCD∩平面AA1B1B
=AB,平面AA1B1B∩平面α=A1B1,所以AB∥A1B1.同理CD∥C1D1,AD∥A1D1,BC∥B1C1.因为四边形A1B1C1D1是平行四边形,所以A1B1∥C1D1,A1D1∥B1C1,所以AB∥CD,
AD∥BC.故四边形ABCD是平行四边形.
图8-5-28
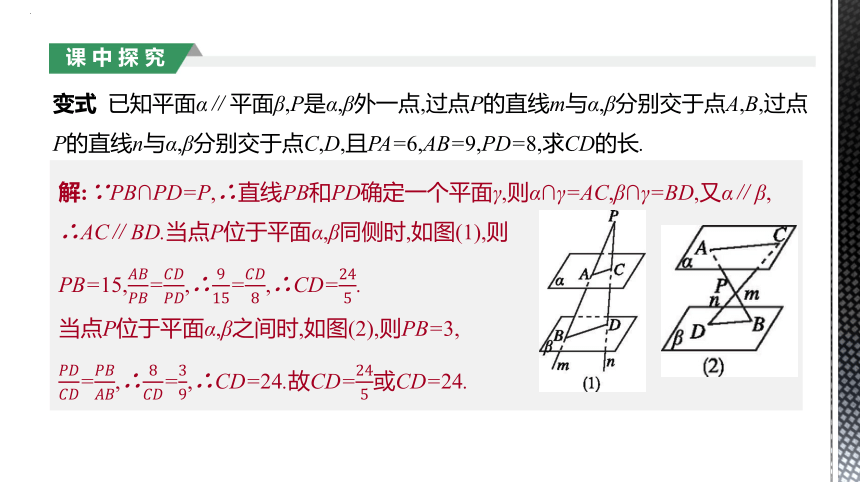
变式 已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于点A,B,过点P的直线n与α,β分别交于点C,D,且PA=6,AB=9,PD=8,求CD的长.
课 中 探 究
解:∵PB∩PD=P,∴直线PB和PD确定一个平面γ,则α∩γ=AC,β∩γ=BD,又α∥β,
∴AC∥BD.当点P位于平面α,β同侧时,如图(1),则
PB=15,=,∴=,∴CD=.
当点P位于平面α,β之间时,如图(2),则PB=3,
=,∴=,∴CD=24.故CD=或CD=24.
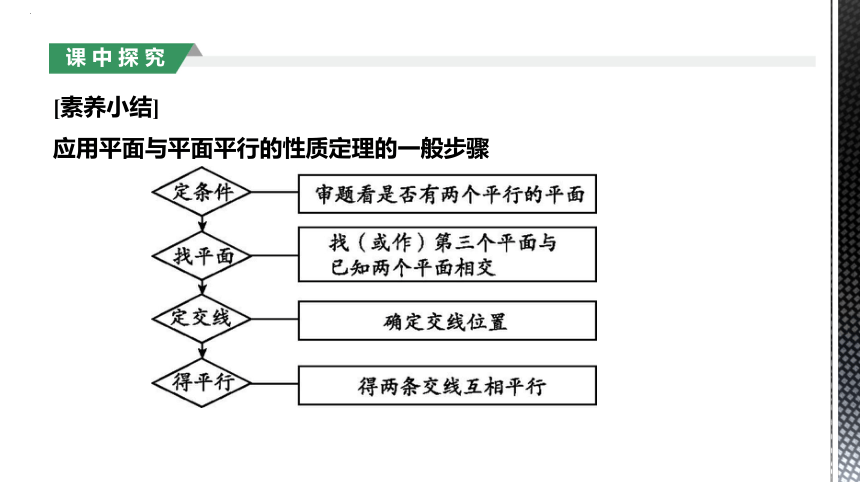
[素养小结]
应用平面与平面平行的性质定理的一般步骤
课 中 探 究
拓展 如图8-5-29,已知平面α∥平面β∥平面γ,且β位于α与γ
之间.A,D∈α,C,F∈γ,AC∩β=B,AF∩β=M,DF∩β=E.
(1)求证:=.
课 中 探 究
图8-5-29
解:(1)证明:∵β∥γ,平面ACF∩β=BM,平面ACF∩γ=CF,
∴BM∥CF,∴=.
同理=.故=.
(2)设AD与CF不平行,且A,C,D,F为定点,α与β间的距离为h’,α与γ间的距离为h,当的值是多少时,△BEM的面积最大
课 中 探 究
解:(2)由(1)知BM∥CF,∴==.同理=.故S△BEM=BM·ME·sin∠BME
=CF·AD·(1-)·sin∠BME,由题意知,AD与CF异面,只有β在α,γ间变化位置,
CF,AD的长是定值,sin∠BME是AD与CF所成角的正弦值,也是定值.
∵(1-)=-()2=-(-)2+≤,当且仅当=时等号成立,此时S△BEM最大,
∴当=,即β在α,γ两平面的中间时,△BEM的面积最大.
探究点二 平行关系的综合应用
[探索] 线线平行、线面平行、面面平行之间有怎样的相互转化关系
课 中 探 究
解:线线平行、线面平行、面面平行之间的相互转化关系如图所示.
例2 如图8-5-30所示,在棱长为2的正方体ABCD -A1B1C1D1中,A1B1的中点是P,过点A1作与平面PBC1平行的截面,求截面的面积.
课 中 探 究
解:记过点A1与平面PBC1平行的截面为β,并记β∩平面A1B1C1D1=n,β∩平面ABB1A1=m.∵β∥平面PBC1,
β∩平面A1B1C1D1=n,平面PBC1∩平面A1B1C1D1=
PC1,∴PC1∥n.同理PB∥m.记n∩C1D1=N,m∩AB=M,则N,M分别为C1D1,AB的中点.连接MC,NC,在正方体ABCD -A1B1C1D1中, ∵P,M分别为A1B1,AB的中点,
图8-5-30
例2 如图8-5-30所示,在棱长为2的正方体ABCD -A1B1C1D1中,A1B1的中点是P,过点A1作与平面PBC1平行的截面,求截面的面积.
课 中 探 究
∴PC1∥MC,又A1N∥PC1,∴A1N∥MC.同理A1M∥NC.
∴点C与点A1,M,N共面,则截面β为平行四边形A1MCN.连接MN,作A1H⊥MN于点H.由题意,易得A1M=A1N=,
MN=2,∴四边形A1MCN是菱形,MH=NH=,
∴A1H=.故截面的面积为=2=2××2×=2.
图8-5-30
变式 如图8-5-31,AB是圆O的直径,C是圆O上异于A,B的点,P为平面ABC外一点.设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
课 中 探 究
证明:连接OG并延长,交AC于点M,连接QM,QO.由G为△AOC的重心,得M为AC的中点.由Q为AP的中点,得QM∥PC,因为PC 平面PBC,QM 平面PBC,所以QM∥平面PBC.因为M为AC的中点,O为AB的中点,所以OM∥BC,
又OM 平面PBC,BC 平面PBC,所以OM∥平面PBC.
因为QM∩MO=M,所以平面QMO∥平面PBC,
又QG 平面QMO,所以QG∥平面PBC.
图8-5-31
[素养小结]
(1)立体几何中常见的平行关系是线线平行、线面平行和面面平行,这三种平行关系不是孤立的,而是相互联系、相互转化的.
(2)解决平行关系的综合问题一般通过平行关系的转化实现.
课 中 探 究
拓展 如图8-5-32所示,在正方体ABCD -A1B1C1D1中,E,F,G,H分别为BC,CC1,
C1D1,A1A的中点.
求证:(1)BF∥HD1;
课 中 探 究
证明:(1)取BB1的中点M,连接C1M,HM,
易知四边形HMC1D1是平行四边形,∴HD1∥MC1,
又由已知可得MC1∥BF,∴BF∥HD1.
图8-5-32
拓展 如图8-5-32所示,在正方体ABCD -A1B1C1D1中,E,F,G,H分别为BC,CC1,
C1D1,A1A的中点.
求证:(2)EG∥平面BB1D1D;
课 中 探 究
证明:(2)取BD的中点O,连接OE,D1O,则OE=DC且
OE∥DC.∵D1G=DC且D1G∥DC,∴OE∥D1G且OE=D1G,∴四边形OEGD1是平行四边形,∴GE∥D1O.
∵D1O 平面BB1D1D,EG 平面BB1D1D,∴EG∥平面BB1D1D.
图8-5-32
拓展 如图8-5-32所示,在正方体ABCD -A1B1C1D1中,E,F,G,H分别为BC,CC1,
C1D1,A1A的中点.
求证:(3)平面BDF∥平面HB1D1.
课 中 探 究
证明:(3)由(1)知BF∥HD1,∵BF 平面HB1D1,HD1 平面HB1D1,∴BF∥平面HB1D1.
∵BD∥B1D1,BD 平面HB1D1,B1D1 平面HB1D1,∴BD∥平面HB1D1,又BF∩BD=B,∴平面BDF∥平面HB1D1.
图8-5-32
利用面面平行的性质定理解题的一般步骤:
①先找两个平面,使这两个平面分别经过这两条直线中的一条;
②判定这两个平面平行(此条件有时题目会直接给出);
③再找一个平面,使这两条直线都在这个平面上;
④由定理得出结论.
备 课 素 材
[例] 如图,正方体ABCD -A1B1C1D1的棱长为2,E,F分别为AA1,AB的中点,点M是正方形ABB1A1内的动点,若C1M∥平面CD1EF,则点M的轨迹长度为( )
A. B.2 C.2 D.4
备 课 素 材
A
备 课 素 材
[解析] 如图所示,取A1B1的中点H,B1B的中点G,连接GH,C1H,C1G,EG,HF.可得四边形EGC1D1是平行四边形,∴C1G∥D1E.∵C1G 平面CD1EF,D1E 平面CD1EF,∴C1G∥平面CD1EF.同理C1H∥平面CD1EF.
∵C1H∩C1G=C1,∴平面C1GH∥平面CD1EF.
∵点M是正方形ABB1A1内的动点,C1M∥平面CD1EF,
∴点M在线段GH上,∴点M的轨迹长度为
GH==.故选A.
1.平面α与圆台的上、下底面分别相交于直线m,n,则m,n的位置关系是 ( )
A.相交 B.异面 C.平行 D.平行或异面
课 堂 评 价
C
2.若平面α∥平面β,直线a 平面α,点B∈β,则在平面β内过点B的所有直线中 ( )
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.存在唯一一条与a平行的直线
课 堂 评 价
[解析] 显然B a,则由点B与直线a可以唯一确定一个平面,记为γ,记γ∩β=b,则B∈b,直线b由γ与β唯一确定,
∵α∥β,α∩γ=a,β∩γ=b,∴a∥b.故选D.
D
3.如果平面α∥平面β,夹在α和β间的两条线段相等,那么这两条线段所在直线的位置关系是 ( )
A.平行 B.相交 C.异面 D.平行、相交或异面
课 堂 评 价
[解析] 如图所示,在正方体ABCD -A1B1C1D1中,易知平面ABCD∥平面A1B1C1D1.对于AA1=BB1,可得直线AA1∥直线BB1;对于A1D=A1B,可得直线A1D∩直线A1B=A1;对于AD1=A1B,可得直线AD1与直线A1B异面.故选D.
D
4.已知平面α∥平面β∥平面γ,过同一点P的两条直线l,m分别与平面α,β,γ相交于点A,B,C和D,E,F,若AB=6,
=,则AC= .
课 堂 评 价
[解析] ∵α∥β∥γ,∴根据面面平行的性质定理可知AD∥BE∥CF,∴=.由=,得=,∵AB=6,∴AC=15.
15
5.如图8-5-33所示,已知正方体ABCD -A1B1C1D1的棱长为3,点E在A1B1上,且B1E=1,记图中阴影平面为平面α,且平面α∥平面BC1E.若平面α∩平面AA1B1B=A1F,求AF的长.
课 堂 评 价
图8-5-33
解:因为平面α∥平面BC1E,平面α∩平面AA1B1B=A1F,平面BC1E∩平面AA1B1B=BE,所以A1F∥BE.又因为A1E∥BF,所以四边形A1EBF是平行四边形.在棱长为3的正方体ABCD -A1B1C1D1中,因为B1E=1,所以BF=A1E=2,所以AF=1.
平面与平面平行的性质
【目标认知】
课程标准 学业要求
从平面与平面平行的定义和基本事实出发,借助长方体,通过直观感知,了解空间中平面与平面的平行关系,归纳出平面与平面平行的性质定理,并加以证明 1.通过直观感知、操作确认,能够归纳出平面与平面平行的性质定理,并能够证明.
2.能够运用性质定理证明一些空间位置关系的简单命题
文字语言 图形语言 符号语言 巧记方法
两个平面 ,如果另一个平面与这两个平面相交,那么两条交线 a∥b 面面平行
知识点 两个平面平行的性质定理
平行
平行
课 前 预 习
线线平行
【诊断分析】 1.判断下列说法的正误.(正确的打“√”,错误的打“×”)
(1)如果两个平面分别平行于第三个平面,那么这两个平面平行. ( )
(2)若两个平面平行,则两个平面内的所有直线都相互平行. ( )
(3)若两个平面平行,则其中一个平面内的直线必平行于另一个平面. ( )
√
课 前 预 习
×
[解析]因为两个平面平行,所以分别在两个平面内的两条直线无公共点,它们平行或异面.
√
2.夹在两个平面间的三条线段,若它们平行且相等,试讨论这两个平面的位置关系.
课 前 预 习
解:如图所示,易知这两个平面的位置关系为平行或相交.
平面与平面平行的性质定理解读
(1)平面与平面平行的性质定理可简述为“若面面平行,则线线平行”.
(2)夹在两个平行平面间的平行线段长度相等.
(3)经过平面外一点,有且仅有一个平面和已知平面平行.
(4)若两个平面平行于第三个平面,则这两个平面互相平行.
备 课 素 材
探究点一 面面平行的性质定理的应用
例1 如图8-5-28所示,四边形ABCD所在的平面与平面α平行,且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形.求证:四边形ABCD是平行四边形.(注:平行投影的投影线互相平行)
课 中 探 究
证明:因为平面ABCD∥平面α,平面ABCD∩平面AA1B1B
=AB,平面AA1B1B∩平面α=A1B1,所以AB∥A1B1.同理CD∥C1D1,AD∥A1D1,BC∥B1C1.因为四边形A1B1C1D1是平行四边形,所以A1B1∥C1D1,A1D1∥B1C1,所以AB∥CD,
AD∥BC.故四边形ABCD是平行四边形.
图8-5-28
变式 已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于点A,B,过点P的直线n与α,β分别交于点C,D,且PA=6,AB=9,PD=8,求CD的长.
课 中 探 究
解:∵PB∩PD=P,∴直线PB和PD确定一个平面γ,则α∩γ=AC,β∩γ=BD,又α∥β,
∴AC∥BD.当点P位于平面α,β同侧时,如图(1),则
PB=15,=,∴=,∴CD=.
当点P位于平面α,β之间时,如图(2),则PB=3,
=,∴=,∴CD=24.故CD=或CD=24.
[素养小结]
应用平面与平面平行的性质定理的一般步骤
课 中 探 究
拓展 如图8-5-29,已知平面α∥平面β∥平面γ,且β位于α与γ
之间.A,D∈α,C,F∈γ,AC∩β=B,AF∩β=M,DF∩β=E.
(1)求证:=.
课 中 探 究
图8-5-29
解:(1)证明:∵β∥γ,平面ACF∩β=BM,平面ACF∩γ=CF,
∴BM∥CF,∴=.
同理=.故=.
(2)设AD与CF不平行,且A,C,D,F为定点,α与β间的距离为h’,α与γ间的距离为h,当的值是多少时,△BEM的面积最大
课 中 探 究
解:(2)由(1)知BM∥CF,∴==.同理=.故S△BEM=BM·ME·sin∠BME
=CF·AD·(1-)·sin∠BME,由题意知,AD与CF异面,只有β在α,γ间变化位置,
CF,AD的长是定值,sin∠BME是AD与CF所成角的正弦值,也是定值.
∵(1-)=-()2=-(-)2+≤,当且仅当=时等号成立,此时S△BEM最大,
∴当=,即β在α,γ两平面的中间时,△BEM的面积最大.
探究点二 平行关系的综合应用
[探索] 线线平行、线面平行、面面平行之间有怎样的相互转化关系
课 中 探 究
解:线线平行、线面平行、面面平行之间的相互转化关系如图所示.
例2 如图8-5-30所示,在棱长为2的正方体ABCD -A1B1C1D1中,A1B1的中点是P,过点A1作与平面PBC1平行的截面,求截面的面积.
课 中 探 究
解:记过点A1与平面PBC1平行的截面为β,并记β∩平面A1B1C1D1=n,β∩平面ABB1A1=m.∵β∥平面PBC1,
β∩平面A1B1C1D1=n,平面PBC1∩平面A1B1C1D1=
PC1,∴PC1∥n.同理PB∥m.记n∩C1D1=N,m∩AB=M,则N,M分别为C1D1,AB的中点.连接MC,NC,在正方体ABCD -A1B1C1D1中, ∵P,M分别为A1B1,AB的中点,
图8-5-30
例2 如图8-5-30所示,在棱长为2的正方体ABCD -A1B1C1D1中,A1B1的中点是P,过点A1作与平面PBC1平行的截面,求截面的面积.
课 中 探 究
∴PC1∥MC,又A1N∥PC1,∴A1N∥MC.同理A1M∥NC.
∴点C与点A1,M,N共面,则截面β为平行四边形A1MCN.连接MN,作A1H⊥MN于点H.由题意,易得A1M=A1N=,
MN=2,∴四边形A1MCN是菱形,MH=NH=,
∴A1H=.故截面的面积为=2=2××2×=2.
图8-5-30
变式 如图8-5-31,AB是圆O的直径,C是圆O上异于A,B的点,P为平面ABC外一点.设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
课 中 探 究
证明:连接OG并延长,交AC于点M,连接QM,QO.由G为△AOC的重心,得M为AC的中点.由Q为AP的中点,得QM∥PC,因为PC 平面PBC,QM 平面PBC,所以QM∥平面PBC.因为M为AC的中点,O为AB的中点,所以OM∥BC,
又OM 平面PBC,BC 平面PBC,所以OM∥平面PBC.
因为QM∩MO=M,所以平面QMO∥平面PBC,
又QG 平面QMO,所以QG∥平面PBC.
图8-5-31
[素养小结]
(1)立体几何中常见的平行关系是线线平行、线面平行和面面平行,这三种平行关系不是孤立的,而是相互联系、相互转化的.
(2)解决平行关系的综合问题一般通过平行关系的转化实现.
课 中 探 究
拓展 如图8-5-32所示,在正方体ABCD -A1B1C1D1中,E,F,G,H分别为BC,CC1,
C1D1,A1A的中点.
求证:(1)BF∥HD1;
课 中 探 究
证明:(1)取BB1的中点M,连接C1M,HM,
易知四边形HMC1D1是平行四边形,∴HD1∥MC1,
又由已知可得MC1∥BF,∴BF∥HD1.
图8-5-32
拓展 如图8-5-32所示,在正方体ABCD -A1B1C1D1中,E,F,G,H分别为BC,CC1,
C1D1,A1A的中点.
求证:(2)EG∥平面BB1D1D;
课 中 探 究
证明:(2)取BD的中点O,连接OE,D1O,则OE=DC且
OE∥DC.∵D1G=DC且D1G∥DC,∴OE∥D1G且OE=D1G,∴四边形OEGD1是平行四边形,∴GE∥D1O.
∵D1O 平面BB1D1D,EG 平面BB1D1D,∴EG∥平面BB1D1D.
图8-5-32
拓展 如图8-5-32所示,在正方体ABCD -A1B1C1D1中,E,F,G,H分别为BC,CC1,
C1D1,A1A的中点.
求证:(3)平面BDF∥平面HB1D1.
课 中 探 究
证明:(3)由(1)知BF∥HD1,∵BF 平面HB1D1,HD1 平面HB1D1,∴BF∥平面HB1D1.
∵BD∥B1D1,BD 平面HB1D1,B1D1 平面HB1D1,∴BD∥平面HB1D1,又BF∩BD=B,∴平面BDF∥平面HB1D1.
图8-5-32
利用面面平行的性质定理解题的一般步骤:
①先找两个平面,使这两个平面分别经过这两条直线中的一条;
②判定这两个平面平行(此条件有时题目会直接给出);
③再找一个平面,使这两条直线都在这个平面上;
④由定理得出结论.
备 课 素 材
[例] 如图,正方体ABCD -A1B1C1D1的棱长为2,E,F分别为AA1,AB的中点,点M是正方形ABB1A1内的动点,若C1M∥平面CD1EF,则点M的轨迹长度为( )
A. B.2 C.2 D.4
备 课 素 材
A
备 课 素 材
[解析] 如图所示,取A1B1的中点H,B1B的中点G,连接GH,C1H,C1G,EG,HF.可得四边形EGC1D1是平行四边形,∴C1G∥D1E.∵C1G 平面CD1EF,D1E 平面CD1EF,∴C1G∥平面CD1EF.同理C1H∥平面CD1EF.
∵C1H∩C1G=C1,∴平面C1GH∥平面CD1EF.
∵点M是正方形ABB1A1内的动点,C1M∥平面CD1EF,
∴点M在线段GH上,∴点M的轨迹长度为
GH==.故选A.
1.平面α与圆台的上、下底面分别相交于直线m,n,则m,n的位置关系是 ( )
A.相交 B.异面 C.平行 D.平行或异面
课 堂 评 价
C
2.若平面α∥平面β,直线a 平面α,点B∈β,则在平面β内过点B的所有直线中 ( )
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.存在唯一一条与a平行的直线
课 堂 评 价
[解析] 显然B a,则由点B与直线a可以唯一确定一个平面,记为γ,记γ∩β=b,则B∈b,直线b由γ与β唯一确定,
∵α∥β,α∩γ=a,β∩γ=b,∴a∥b.故选D.
D
3.如果平面α∥平面β,夹在α和β间的两条线段相等,那么这两条线段所在直线的位置关系是 ( )
A.平行 B.相交 C.异面 D.平行、相交或异面
课 堂 评 价
[解析] 如图所示,在正方体ABCD -A1B1C1D1中,易知平面ABCD∥平面A1B1C1D1.对于AA1=BB1,可得直线AA1∥直线BB1;对于A1D=A1B,可得直线A1D∩直线A1B=A1;对于AD1=A1B,可得直线AD1与直线A1B异面.故选D.
D
4.已知平面α∥平面β∥平面γ,过同一点P的两条直线l,m分别与平面α,β,γ相交于点A,B,C和D,E,F,若AB=6,
=,则AC= .
课 堂 评 价
[解析] ∵α∥β∥γ,∴根据面面平行的性质定理可知AD∥BE∥CF,∴=.由=,得=,∵AB=6,∴AC=15.
15
5.如图8-5-33所示,已知正方体ABCD -A1B1C1D1的棱长为3,点E在A1B1上,且B1E=1,记图中阴影平面为平面α,且平面α∥平面BC1E.若平面α∩平面AA1B1B=A1F,求AF的长.
课 堂 评 价
图8-5-33
解:因为平面α∥平面BC1E,平面α∩平面AA1B1B=A1F,平面BC1E∩平面AA1B1B=BE,所以A1F∥BE.又因为A1E∥BF,所以四边形A1EBF是平行四边形.在棱长为3的正方体ABCD -A1B1C1D1中,因为B1E=1,所以BF=A1E=2,所以AF=1.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
