苏教版五年级上学期数学第七单元7解决问题的策略 课件 (共16张PPT)
文档属性
| 名称 | 苏教版五年级上学期数学第七单元7解决问题的策略 课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 13:01:03 | ||
图片预览






文档简介
(共16张PPT)
解决问题的策略
温故知新
(1)一组一组地写出16可以分成几和几。
(2)用12个边长是1厘米的正方形拼成不同的长方形。
(3)用3张数字卡片8、5、4有序地写出能组成的所
有的三位数。
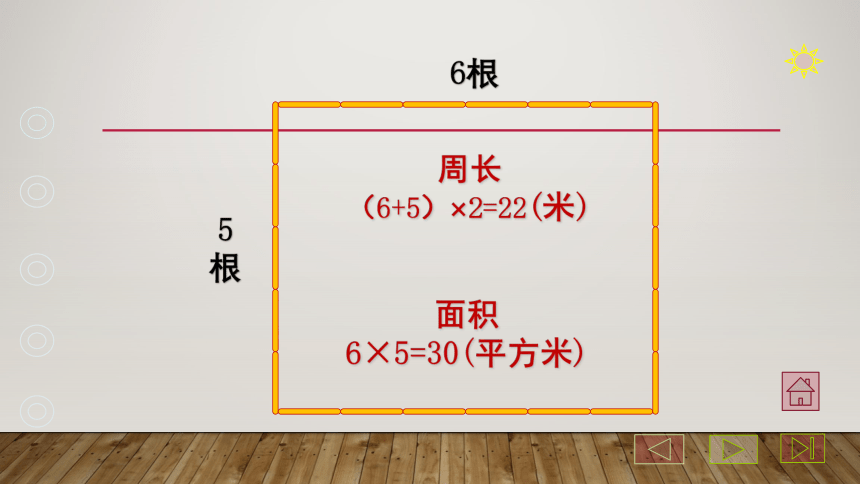
6根
5
根
面积
6×5=30(平方米)
周长
(6+5)×2=22(米)
合作探究
填表时是从长是几米的长方形开始想起的?为什么要从长是10米的长方形开始想起?
周长为22米的长方形,它的长和宽的和一定是22÷2=11(米)。由此可知,围成的长方形的长最多是10米。
根据列举的结果,你知道怎样围面积最大吗?
类型一:列举法解决实际问题
例:用36个1平方厘米的正方形拼成长方形(或正方形),有多少种不同的拼法?它们的周长各是多少?
长/米 36 18 12 9 6
宽/米 1 2 3 4 6
周长/米 74 40 30 26 24
共有5种不同的拼法。
面积固定36平方厘米
面积一定
面积一定时,长和宽越接近,所围成图形的周长最小。
自主练习
一共要通3次电话。
一共要寄6张贺卡。
小强、小华和小丽是好朋友,如果他们每两人通一次电话,一共要通多少次电话?如果他们互相寄一张节目贺卡,一共要寄多少张贺卡?
火眼金睛
长/米 8 10 6 9 20 7 5
宽/米 3 1 5 2 1 4 6
面积/平方米 24 10 30 18 20 28 30
自主练习
4×9=36
2×18=36
3×12=36
1×36=36
6×6=36
交换因数的位置后一共有9个
两个自然数相乘,积是36的算式有多少个?
类型 用画图法解决实际问题
例:南山中心小学举行小学生足球比赛,有4支队伍参加,分别是红队、黄队、绿队和蓝队。如果每两支队伍比赛一场,一共要比赛多少场?
红队
绿队
黄队
蓝队
由上图可知,要比赛6场
巩固训练
1、一个音乐钟,每隔一段相等的时间就发出铃声。已经知道上午9:00、9:40、10:20和11:00发出铃声,那么下面哪些时间也会发出铃声?
13:00
14:40
15:40
16:00
知识点:用列举的策略解决实际问题
1.用列举法解决围长方形的最大面积问题
先求出长方形的长与宽的和,再列表找出不同的围法﹔对列举的结果进行比较,找到符合要求的答案。
2.用列举的策略解决比赛场次问题
(1)文字列举:列举每次比赛场次的组合。
(2)画图列举:几支球队就画几个点,再用两点之间的连线表示球队之间所进行的比赛,连线有几条,就有几场比赛。
变式:
用3,0,5这三张数字卡片可以组成( )个不同的三位数。
4
百位是3:
305 , 350
百位是5:
503 , 530
从农场回家,有一公交站台,可现在已经是下午了,你会选择以下哪个时间去坐公交车比较合适呢?
a14:40 b15:20 c16:20 d16:40
发车时间
9:00
9:40
10:20
11:00
……
9:40
9:00
10:20
11:00
11:40
12:20
13:00
13:40
14:20
15:00
15:40
16:20
从1—12这十二个自然数中选取3个不同的数,使得这3个不同的数的和等于26.共有多少种不同的选取方法?
应用:
26=12+11+3;26=12+10+4;26=12+9+5;26=12+8+6(4种)
26=11+10+5;26=11+9+6;26=11+8+7;(3种)
26=10+9+7;(1种)
4+3+1=8(种)
先固定一个
课堂小结
同学们,本节课你学会了什么?
同学们再见
解决问题的策略
温故知新
(1)一组一组地写出16可以分成几和几。
(2)用12个边长是1厘米的正方形拼成不同的长方形。
(3)用3张数字卡片8、5、4有序地写出能组成的所
有的三位数。
6根
5
根
面积
6×5=30(平方米)
周长
(6+5)×2=22(米)
合作探究
填表时是从长是几米的长方形开始想起的?为什么要从长是10米的长方形开始想起?
周长为22米的长方形,它的长和宽的和一定是22÷2=11(米)。由此可知,围成的长方形的长最多是10米。
根据列举的结果,你知道怎样围面积最大吗?
类型一:列举法解决实际问题
例:用36个1平方厘米的正方形拼成长方形(或正方形),有多少种不同的拼法?它们的周长各是多少?
长/米 36 18 12 9 6
宽/米 1 2 3 4 6
周长/米 74 40 30 26 24
共有5种不同的拼法。
面积固定36平方厘米
面积一定
面积一定时,长和宽越接近,所围成图形的周长最小。
自主练习
一共要通3次电话。
一共要寄6张贺卡。
小强、小华和小丽是好朋友,如果他们每两人通一次电话,一共要通多少次电话?如果他们互相寄一张节目贺卡,一共要寄多少张贺卡?
火眼金睛
长/米 8 10 6 9 20 7 5
宽/米 3 1 5 2 1 4 6
面积/平方米 24 10 30 18 20 28 30
自主练习
4×9=36
2×18=36
3×12=36
1×36=36
6×6=36
交换因数的位置后一共有9个
两个自然数相乘,积是36的算式有多少个?
类型 用画图法解决实际问题
例:南山中心小学举行小学生足球比赛,有4支队伍参加,分别是红队、黄队、绿队和蓝队。如果每两支队伍比赛一场,一共要比赛多少场?
红队
绿队
黄队
蓝队
由上图可知,要比赛6场
巩固训练
1、一个音乐钟,每隔一段相等的时间就发出铃声。已经知道上午9:00、9:40、10:20和11:00发出铃声,那么下面哪些时间也会发出铃声?
13:00
14:40
15:40
16:00
知识点:用列举的策略解决实际问题
1.用列举法解决围长方形的最大面积问题
先求出长方形的长与宽的和,再列表找出不同的围法﹔对列举的结果进行比较,找到符合要求的答案。
2.用列举的策略解决比赛场次问题
(1)文字列举:列举每次比赛场次的组合。
(2)画图列举:几支球队就画几个点,再用两点之间的连线表示球队之间所进行的比赛,连线有几条,就有几场比赛。
变式:
用3,0,5这三张数字卡片可以组成( )个不同的三位数。
4
百位是3:
305 , 350
百位是5:
503 , 530
从农场回家,有一公交站台,可现在已经是下午了,你会选择以下哪个时间去坐公交车比较合适呢?
a14:40 b15:20 c16:20 d16:40
发车时间
9:00
9:40
10:20
11:00
……
9:40
9:00
10:20
11:00
11:40
12:20
13:00
13:40
14:20
15:00
15:40
16:20
从1—12这十二个自然数中选取3个不同的数,使得这3个不同的数的和等于26.共有多少种不同的选取方法?
应用:
26=12+11+3;26=12+10+4;26=12+9+5;26=12+8+6(4种)
26=11+10+5;26=11+9+6;26=11+8+7;(3种)
26=10+9+7;(1种)
4+3+1=8(种)
先固定一个
课堂小结
同学们,本节课你学会了什么?
同学们再见
