沪科版数学七年级下册 第8章 《单项式与单项式相乘(1)》课件(共12张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 第8章 《单项式与单项式相乘(1)》课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 16:37:02 | ||
图片预览



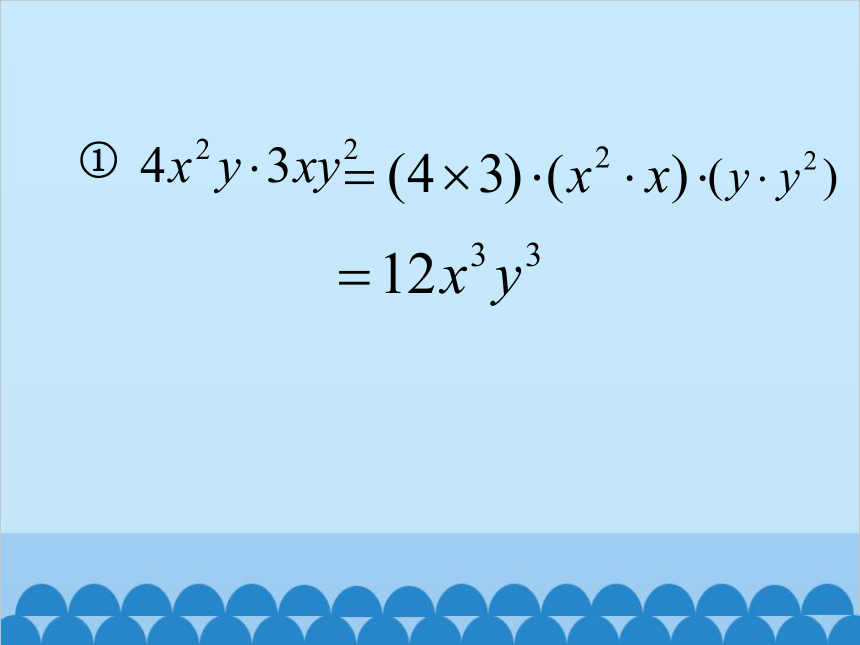
文档简介
(共13张PPT)
8.2 整式乘法
1.单项式与单项式相乘
知识回顾
(1)同底数幂乘法:
(2)幂的乘方:
(3)积的乘方:
(4)同底数幂相除:
(5)乘法交换律:
(6)乘法结合律:
问题1 光的速度约为3×105km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年才能到达地球。一年以3×107s计算,试问地球与这颗恒星的距离约为多少千米?
分析:距离=速度×时间;
则太阳与比邻星的距离为:
(3×105)×(4 ×3 ×107)
=(3 ×4 ×3) ×(105 ×107)
=36 ×1012
=3.6 ×1013(千米)
课程导入
速度: 3×105km/s
时间:4×3×107s
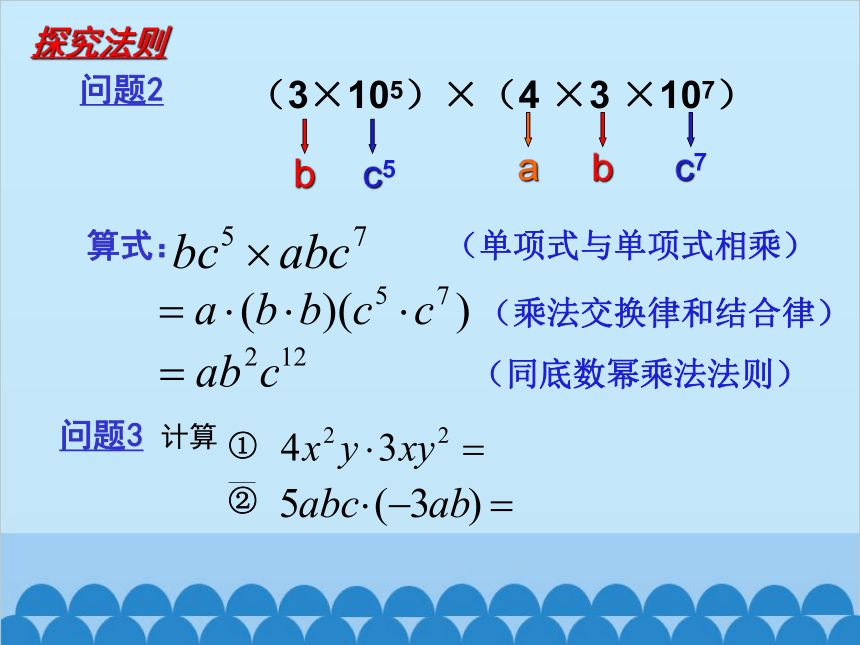
问题2
(3×105)×(4 ×3 ×107)
b
b
c5
c7
a
算式:
(单项式与单项式相乘)
(乘法交换律和结合律)
(同底数幂乘法法则)
①
探究法则
问题3 计算
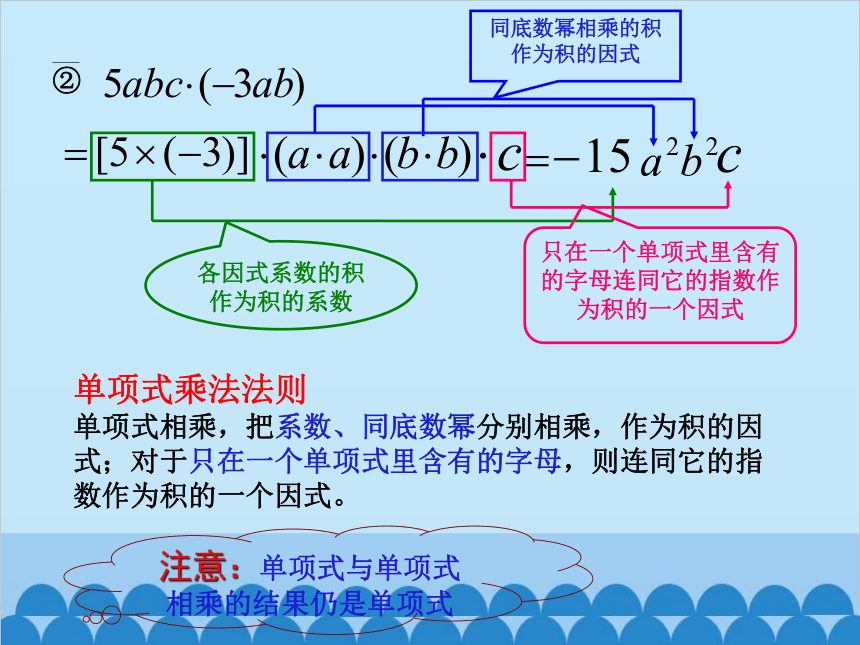
②
①
②
各因式系数的积作为积的系数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
同底数幂相乘的积作为积的因式
单项式乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
注意:单项式与单项式相乘的结果仍是单项式
法则应用
例1 计算:(1)
(2)
(3)
解:
(2)
(3)
(1)
1、有乘方先算乘方
2、单项式乘法法则对于三个以上的单项式相乘同样适用
课堂小结
1、单项式乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
注意:单项式相乘的结果仍是单项式
2、计算步骤
有乘方先算乘方,然后再相乘
(2)把系数的积作为积的系数
(3)同底数幂相乘的积作为积的因式
(4)只在一个单项式里含有的字母,要连同它的指数写在积里
下面的计算对不 对?如果不对,怎样改正?
⑴
⑷
⑶
⑵
⑸
我是法官我来判
?
精心选一选:
1、下列计算中,正确的是( )
A、2a3·3a2=6a6 B、4x3·2x5=8x8
C、2X·2X5=4X5 D、5X3·4X4=9X7
2、下列运算正确的是( )
A、X2·X3=X6 B、X2+X2=2X4
C、(-2X)2=-4X2 D、(-2X2)(-3X3)=6x5
B
D
(各组派一代表)
解:原式
继续探究
计算
相比较前面的计算,这道题多了什么运算
(先乘方,再做单项式相乘)
8.2 整式乘法
1.单项式与单项式相乘
知识回顾
(1)同底数幂乘法:
(2)幂的乘方:
(3)积的乘方:
(4)同底数幂相除:
(5)乘法交换律:
(6)乘法结合律:
问题1 光的速度约为3×105km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年才能到达地球。一年以3×107s计算,试问地球与这颗恒星的距离约为多少千米?
分析:距离=速度×时间;
则太阳与比邻星的距离为:
(3×105)×(4 ×3 ×107)
=(3 ×4 ×3) ×(105 ×107)
=36 ×1012
=3.6 ×1013(千米)
课程导入
速度: 3×105km/s
时间:4×3×107s
问题2
(3×105)×(4 ×3 ×107)
b
b
c5
c7
a
算式:
(单项式与单项式相乘)
(乘法交换律和结合律)
(同底数幂乘法法则)
①
探究法则
问题3 计算
②
①
②
各因式系数的积作为积的系数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
同底数幂相乘的积作为积的因式
单项式乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
注意:单项式与单项式相乘的结果仍是单项式
法则应用
例1 计算:(1)
(2)
(3)
解:
(2)
(3)
(1)
1、有乘方先算乘方
2、单项式乘法法则对于三个以上的单项式相乘同样适用
课堂小结
1、单项式乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
注意:单项式相乘的结果仍是单项式
2、计算步骤
有乘方先算乘方,然后再相乘
(2)把系数的积作为积的系数
(3)同底数幂相乘的积作为积的因式
(4)只在一个单项式里含有的字母,要连同它的指数写在积里
下面的计算对不 对?如果不对,怎样改正?
⑴
⑷
⑶
⑵
⑸
我是法官我来判
?
精心选一选:
1、下列计算中,正确的是( )
A、2a3·3a2=6a6 B、4x3·2x5=8x8
C、2X·2X5=4X5 D、5X3·4X4=9X7
2、下列运算正确的是( )
A、X2·X3=X6 B、X2+X2=2X4
C、(-2X)2=-4X2 D、(-2X2)(-3X3)=6x5
B
D
(各组派一代表)
解:原式
继续探究
计算
相比较前面的计算,这道题多了什么运算
(先乘方,再做单项式相乘)
