粤教版(2019)1.2进制与进制转换 课件
文档属性
| 名称 | 粤教版(2019)1.2进制与进制转换 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-06-02 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
进制与进制转换
于是,就出现了进位的思想,到第十段绳子的时候我就打一个结,这样表示很多数字就非常方便了,这就是进制的雏形,那大家再想一下为什么是到第十段绳子才进位呢?
进制的由来
思考:结绳记数是人类早期用来记数的方法之一,1段绳即代表1个数,那如果有很多数字怎么办呢?
古人“结绳记数”
十进制的由来
很久很久以前,黄帝和蚩尤之间发生了场激烈的战斗,经过大家共同的努力,黄帝大获全胜。
于是,黄帝部落的人开始对所有的蚩尤残兵败将和物品进行清点。清点的工作由黄帝部落管理仓库的邪曷(hé)进行。他把每个战俘对应着自己的一个手指,一根指头代表一个战俘,两根指头代表两个战俘……可是人的手指头只有十个,并且这次黄帝部落俘获了很多的俘虏,邪曷的十个手指都用完了也没数完,这该怎么办昵?
正当大家一筹莫展的时候,黄帝的一个部将说:“既然用完了十根手指,我们可以先把已数过的十个俘虏放在一边,用一根绳子捆起来打一个结,表示十个战俘。然后接着用手指数,够十个再放一堆,这样一个结一个结地打下去,我们就知道共俘获了多少俘虏了”。大家都认为这个方法很好,负责统计俘虏的邪曷用这个方法出色地完成了任务。
这就是“逢十进一”的十进制的最早由来。
进制的概念
进制也就是进位计数制,是人为定义的带进位的计数方法。对于任何一种进制—N进制,就表示每一位上的数运算时都是逢N进一。
技术实现简单:计算机是由逻辑电路组成,逻辑电路通常只有两个状态,开关的接通与断开,这两种状态正好可以用“1”和“0”表示
运算规则简单:与十进制数相比,二进制数的运算规则要简单得多,这不仅可以使运算器的结构得到简化,而且有利于提高运算速度
适合逻辑运算:逻辑代数是逻辑运算的理论依据,二进制只有两个数码,正好与逻辑代数中的“真”和“假”相吻合。
……
常见的进制
我们人类使用十进制,计算机使用二进制,常见的还有八进制、十六进制
计算机内部采用二进制的主要原因:
二进制
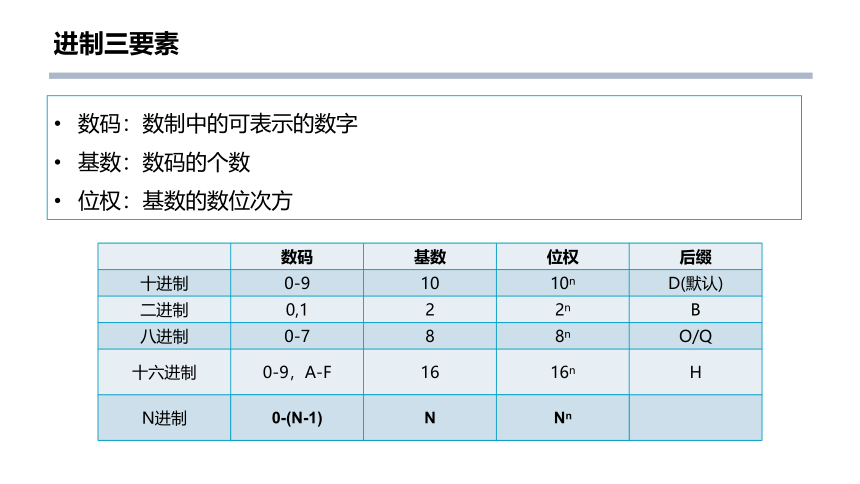
进制三要素
数码:数制中的可表示的数字
基数:数码的个数
位权:基数的数位次方
数码 基数 位权 后缀
十进制 0-9 10 10n D(默认)
二进制 0,1 2 2n B
八进制 0-7 8 8n O/Q
十六进制 0-9,A-F 16 16n H
N进制
0-(N-1) N Nn
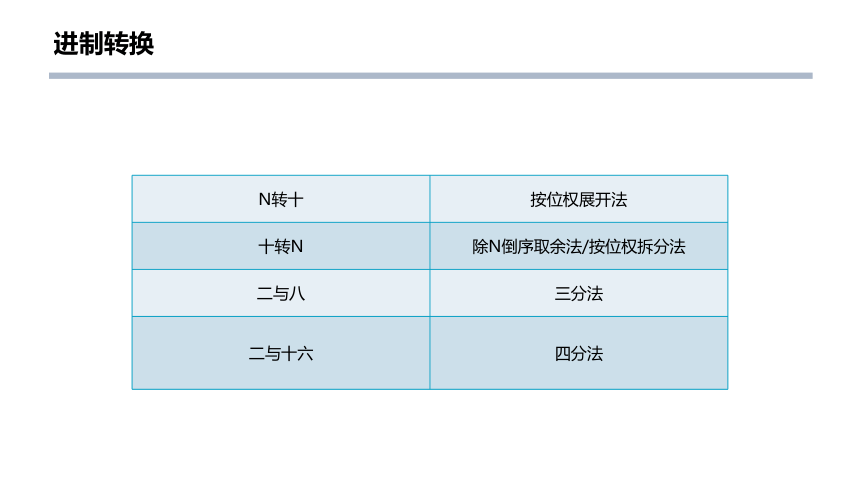
进制转换
N转十 按位权展开法
十转N 除N倒序取余法/按位权拆分法
二与八 三分法
二与十六 四分法
按位权展开法
N进制转十进制
按位权展开法
自右向左依次数位乘以位权展开后相加
N进制的位权从N0开始,依次N1,N2……递增
例:(1101)B = 1 * 20 + 0 * 21 + 1 * 22 + 1 * 23 = 1 + 0 + 4 + 8 = 13
例:(157)Q = 7 * 80 + 5 * 81 + 1 * 82 = 7 + 40 + 64 = 111
例:(3E)H = 14 * 160 + 3 * 161 = 14 + 48 = 62
按位权展开法 - 技巧
技巧:在所有的二进制上面依次标出位权后相加可以快速的求出结果,而无需一个个展开
常见的二次幂 20 21 22 23 24 25 26 27 28 29 210
1 2 4 8 16 32 64 128 256 512 1024
例:(1011)B = 1 0 1 1 = 1 + 2 + 8 = 11
例:(100101)B = 1 0 0 1 0 1 = 1 + 4 + 32 = 37
按位权展开法 - 特殊
特殊:(n个1)B = 2n-1,例如1111B= 24 - 1,根据二进制运算规则的逢2进1,即二进制中1+1=10,可得1111B + 1B = 10000B = 24,故1111B = 10000B - 1B = 24 - 1
例:(1111)B = 24 - 1 = 16 - 1 = 15
例:(11111111)B = 28 - 1 = 256 - 1 = 255
按位权展开法 - 练习
给下列各进制数转换为十进制?
1010 B
1011 B
110101 B
100110 B
12 Q
2A H
10
11
53
38
10
42
除N倒序取余法
十进制转N进制
除N倒序取余法 反复除以N得到商和余数 商继续除N直到为0为止(当X小于N时,X除N等于0余X ) 余数倒序即为结果例:13 = ( 1101)B 127 = (177)Q 127 = (7F)H除N倒序取余法 - 练习
给下列十进制数转换为指定进制?
13 D = ( ) B
1101
65 D = ( ) B
40 D = ( ) Q
58 D = ( ) H
1000001
50
3A
按位权拆分法
适用于十进制转二进制、三分法、四分法
按位权拆分法
应熟练掌握16以内的按位权拆分,即8、4、2、1的组合相加
不要去纠结拆分后的数字是2的几次幂,顺序标出位权后依次填充即可
三分法
二进制与八进制相互转换
三分法
二进制转八进制,以3个二进制为一个组,每组转换为十进制数字
八进制转换二进制,每个数字拆分为3个二进制
在数字前方添加或者减少0不会影响结果
三分法 - 练习
利用三分法完成下列二进制与八进制的相互转换?
100101 B = ( ) Q
45
11101 B = ( ) Q
67 Q = ( ) B
123 Q = ( ) B
35
110111
1010011
四分法
二进制与十六进制相互转换
四分法
二进制转十六进制,以4个二进制为一个组,每组转换为十进制数字
八进制转换二进制,每个数字拆分为4个二进制
在数字前方添加或者减少0不会影响结果
四分法 - 练习
利用四分法完成下列二进制与十六进制的相互转换?
101011101B = ()H
15D
11001111B = ()H
ACH = ()B
12FH = ()B
CF
10101100
100101111
总结
进制与进制转换练习作业完成“问卷星”练习题谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
进制与进制转换
于是,就出现了进位的思想,到第十段绳子的时候我就打一个结,这样表示很多数字就非常方便了,这就是进制的雏形,那大家再想一下为什么是到第十段绳子才进位呢?
进制的由来
思考:结绳记数是人类早期用来记数的方法之一,1段绳即代表1个数,那如果有很多数字怎么办呢?
古人“结绳记数”
十进制的由来
很久很久以前,黄帝和蚩尤之间发生了场激烈的战斗,经过大家共同的努力,黄帝大获全胜。
于是,黄帝部落的人开始对所有的蚩尤残兵败将和物品进行清点。清点的工作由黄帝部落管理仓库的邪曷(hé)进行。他把每个战俘对应着自己的一个手指,一根指头代表一个战俘,两根指头代表两个战俘……可是人的手指头只有十个,并且这次黄帝部落俘获了很多的俘虏,邪曷的十个手指都用完了也没数完,这该怎么办昵?
正当大家一筹莫展的时候,黄帝的一个部将说:“既然用完了十根手指,我们可以先把已数过的十个俘虏放在一边,用一根绳子捆起来打一个结,表示十个战俘。然后接着用手指数,够十个再放一堆,这样一个结一个结地打下去,我们就知道共俘获了多少俘虏了”。大家都认为这个方法很好,负责统计俘虏的邪曷用这个方法出色地完成了任务。
这就是“逢十进一”的十进制的最早由来。
进制的概念
进制也就是进位计数制,是人为定义的带进位的计数方法。对于任何一种进制—N进制,就表示每一位上的数运算时都是逢N进一。
技术实现简单:计算机是由逻辑电路组成,逻辑电路通常只有两个状态,开关的接通与断开,这两种状态正好可以用“1”和“0”表示
运算规则简单:与十进制数相比,二进制数的运算规则要简单得多,这不仅可以使运算器的结构得到简化,而且有利于提高运算速度
适合逻辑运算:逻辑代数是逻辑运算的理论依据,二进制只有两个数码,正好与逻辑代数中的“真”和“假”相吻合。
……
常见的进制
我们人类使用十进制,计算机使用二进制,常见的还有八进制、十六进制
计算机内部采用二进制的主要原因:
二进制
进制三要素
数码:数制中的可表示的数字
基数:数码的个数
位权:基数的数位次方
数码 基数 位权 后缀
十进制 0-9 10 10n D(默认)
二进制 0,1 2 2n B
八进制 0-7 8 8n O/Q
十六进制 0-9,A-F 16 16n H
N进制
0-(N-1) N Nn
进制转换
N转十 按位权展开法
十转N 除N倒序取余法/按位权拆分法
二与八 三分法
二与十六 四分法
按位权展开法
N进制转十进制
按位权展开法
自右向左依次数位乘以位权展开后相加
N进制的位权从N0开始,依次N1,N2……递增
例:(1101)B = 1 * 20 + 0 * 21 + 1 * 22 + 1 * 23 = 1 + 0 + 4 + 8 = 13
例:(157)Q = 7 * 80 + 5 * 81 + 1 * 82 = 7 + 40 + 64 = 111
例:(3E)H = 14 * 160 + 3 * 161 = 14 + 48 = 62
按位权展开法 - 技巧
技巧:在所有的二进制上面依次标出位权后相加可以快速的求出结果,而无需一个个展开
常见的二次幂 20 21 22 23 24 25 26 27 28 29 210
1 2 4 8 16 32 64 128 256 512 1024
例:(1011)B = 1 0 1 1 = 1 + 2 + 8 = 11
例:(100101)B = 1 0 0 1 0 1 = 1 + 4 + 32 = 37
按位权展开法 - 特殊
特殊:(n个1)B = 2n-1,例如1111B= 24 - 1,根据二进制运算规则的逢2进1,即二进制中1+1=10,可得1111B + 1B = 10000B = 24,故1111B = 10000B - 1B = 24 - 1
例:(1111)B = 24 - 1 = 16 - 1 = 15
例:(11111111)B = 28 - 1 = 256 - 1 = 255
按位权展开法 - 练习
给下列各进制数转换为十进制?
1010 B
1011 B
110101 B
100110 B
12 Q
2A H
10
11
53
38
10
42
除N倒序取余法
十进制转N进制
除N倒序取余法 反复除以N得到商和余数 商继续除N直到为0为止(当X小于N时,X除N等于0余X ) 余数倒序即为结果例:13 = ( 1101)B 127 = (177)Q 127 = (7F)H除N倒序取余法 - 练习
给下列十进制数转换为指定进制?
13 D = ( ) B
1101
65 D = ( ) B
40 D = ( ) Q
58 D = ( ) H
1000001
50
3A
按位权拆分法
适用于十进制转二进制、三分法、四分法
按位权拆分法
应熟练掌握16以内的按位权拆分,即8、4、2、1的组合相加
不要去纠结拆分后的数字是2的几次幂,顺序标出位权后依次填充即可
三分法
二进制与八进制相互转换
三分法
二进制转八进制,以3个二进制为一个组,每组转换为十进制数字
八进制转换二进制,每个数字拆分为3个二进制
在数字前方添加或者减少0不会影响结果
三分法 - 练习
利用三分法完成下列二进制与八进制的相互转换?
100101 B = ( ) Q
45
11101 B = ( ) Q
67 Q = ( ) B
123 Q = ( ) B
35
110111
1010011
四分法
二进制与十六进制相互转换
四分法
二进制转十六进制,以4个二进制为一个组,每组转换为十进制数字
八进制转换二进制,每个数字拆分为4个二进制
在数字前方添加或者减少0不会影响结果
四分法 - 练习
利用四分法完成下列二进制与十六进制的相互转换?
101011101B = ()H
15D
11001111B = ()H
ACH = ()B
12FH = ()B
CF
10101100
100101111
总结
进制与进制转换练习作业完成“问卷星”练习题谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
