粤教版(2019)1.2进制与进制转换 讲义
文档属性
| 名称 | 粤教版(2019)1.2进制与进制转换 讲义 |
|
|
| 格式 | zip | ||
| 文件大小 | 61.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-06-02 00:00:00 | ||
图片预览

文档简介
进制与进制转换讲义
1、进制
进制也就是进位计数制,是人为定义的带进位的计数方法。对于任何一种进制—N进制,就表示每一位上的数运算时都是逢N进一。
我们人类使用十进制,计算机使用二进制,常见的还有八进制、十六进制
人类使用十进制的原因:人类有十根手指
计算机使用二进制的原因:技术实现简单;运算规则简单;适合逻辑运算
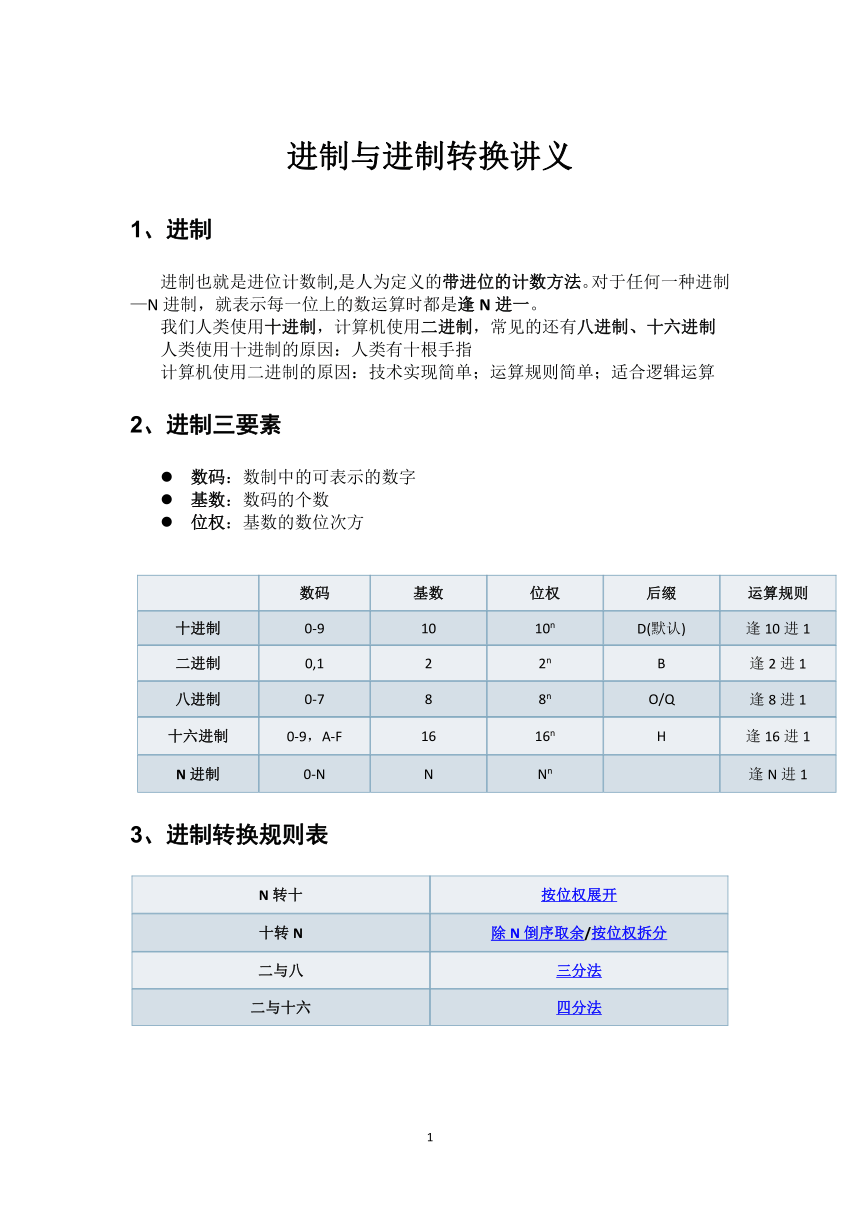
2、进制三要素
数码:数制中的可表示的数字
基数:数码的个数
位权:基数的数位次方
数码 基数 位权 后缀 运算规则
十进制 0-9 10 10n D(默认) 逢10进1
二进制 0,1 2 2n B 逢2进1
八进制 0-7 8 8n O/Q 逢8进1
十六进制 0-9,A-F 16 16n H 逢16进1
N进制 0-N N Nn 逢N进1
3、进制转换规则表
N转十 按位权展开
十转N 除N倒序取余/按位权拆分
二与八 三分法
二与十六 四分法
、
按位权展开法(N进制转十进制)
自右向左依次数位乘以位权展开后相加
N进制的位权从N0开始,依次N1,N2……递增
例:(1101)B = 1 * 20 + 0 * 21 + 1 * 22 + 1 * 23 = 1 + 0 + 4 + 8 = 13
Tip:在所有的二进制上面依次标出位权后相加可以快速的求出结果,而无需一个个展开
常见的二次幂
20 21 22 23 24 25 26 27 28 29 210
1 2 4 8 16 32 64 128 256 512 1024
例:(1011)B = 1 0 1 1 = 1 + 2 + 8 = 11
例:(100101)B = 1 0 0 1 0 1 = 1 + 4 + 32 = 37
例:(157)Q = 7 * 80 + 5 * 81 + 1 * 82 = 7 + 40 + 64 = 111
例:(3E)H = 14 * 160 + 3 * 161 = 14 + 48 = 62
特殊:(n个1)B = 2n-1,例如1111B= 24 - 1,根据二进制运算规则的逢2进1,即二进制中1+1=10,可得1111B + 1B = 10000B = 24,故1111B = 10000B - 1B = 24 - 1
除N倒序取余法(十进制转N进制)
反复除以N得到商和余数
商继续除N直到为0为止(当X小于N时,X除N等于0余X )
余数倒序即为结果
例:13 = ( 1101)B 127 = (177)Q 127 = (7F)H
按位权拆分法(适用十进制转二进制、三分法、四分法)
应熟练掌握16以内的按位权拆分,即8、4、2、1的组合相加
不要去纠结拆分后的数字是2的几次幂,顺序标出位权后依次填充即可
例:13 =8+4+1 = 1 1 0 1 = (1101)B
例:65 = 64 + 1 = 1 0 0 0 0 0 1 = (1000001)B
例:100 = 64 + 32 + 4 = 1 1 0 0 1 0 0 = (1100100)B
三分法(二进制与八进制相互转换)
二进制转八进制,以3个二进制为一个组,每组转换为十进制数字
八进制转换二进制,每个数字拆分为3个二进制
在数字前方添加或者减少0不会影响结果
例:(11100100)B = 011,100,100 = (344)Q
例:(136)Q = 1,2+1,4+2 = 001,011,110 = (1011110)B
8、四分法(二进制与十六进制相互转换)
例:(1011100100)B = 0010,1110,0100 = (2E4)Q
例:(51A) = 4+1,1,8+2 = 0101,0001,1010 = (110011010)B
1、进制
进制也就是进位计数制,是人为定义的带进位的计数方法。对于任何一种进制—N进制,就表示每一位上的数运算时都是逢N进一。
我们人类使用十进制,计算机使用二进制,常见的还有八进制、十六进制
人类使用十进制的原因:人类有十根手指
计算机使用二进制的原因:技术实现简单;运算规则简单;适合逻辑运算
2、进制三要素
数码:数制中的可表示的数字
基数:数码的个数
位权:基数的数位次方
数码 基数 位权 后缀 运算规则
十进制 0-9 10 10n D(默认) 逢10进1
二进制 0,1 2 2n B 逢2进1
八进制 0-7 8 8n O/Q 逢8进1
十六进制 0-9,A-F 16 16n H 逢16进1
N进制 0-N N Nn 逢N进1
3、进制转换规则表
N转十 按位权展开
十转N 除N倒序取余/按位权拆分
二与八 三分法
二与十六 四分法
、
按位权展开法(N进制转十进制)
自右向左依次数位乘以位权展开后相加
N进制的位权从N0开始,依次N1,N2……递增
例:(1101)B = 1 * 20 + 0 * 21 + 1 * 22 + 1 * 23 = 1 + 0 + 4 + 8 = 13
Tip:在所有的二进制上面依次标出位权后相加可以快速的求出结果,而无需一个个展开
常见的二次幂
20 21 22 23 24 25 26 27 28 29 210
1 2 4 8 16 32 64 128 256 512 1024
例:(1011)B = 1 0 1 1 = 1 + 2 + 8 = 11
例:(100101)B = 1 0 0 1 0 1 = 1 + 4 + 32 = 37
例:(157)Q = 7 * 80 + 5 * 81 + 1 * 82 = 7 + 40 + 64 = 111
例:(3E)H = 14 * 160 + 3 * 161 = 14 + 48 = 62
特殊:(n个1)B = 2n-1,例如1111B= 24 - 1,根据二进制运算规则的逢2进1,即二进制中1+1=10,可得1111B + 1B = 10000B = 24,故1111B = 10000B - 1B = 24 - 1
除N倒序取余法(十进制转N进制)
反复除以N得到商和余数
商继续除N直到为0为止(当X小于N时,X除N等于0余X )
余数倒序即为结果
例:13 = ( 1101)B 127 = (177)Q 127 = (7F)H
按位权拆分法(适用十进制转二进制、三分法、四分法)
应熟练掌握16以内的按位权拆分,即8、4、2、1的组合相加
不要去纠结拆分后的数字是2的几次幂,顺序标出位权后依次填充即可
例:13 =8+4+1 = 1 1 0 1 = (1101)B
例:65 = 64 + 1 = 1 0 0 0 0 0 1 = (1000001)B
例:100 = 64 + 32 + 4 = 1 1 0 0 1 0 0 = (1100100)B
三分法(二进制与八进制相互转换)
二进制转八进制,以3个二进制为一个组,每组转换为十进制数字
八进制转换二进制,每个数字拆分为3个二进制
在数字前方添加或者减少0不会影响结果
例:(11100100)B = 011,100,100 = (344)Q
例:(136)Q = 1,2+1,4+2 = 001,011,110 = (1011110)B
8、四分法(二进制与十六进制相互转换)
例:(1011100100)B = 0010,1110,0100 = (2E4)Q
例:(51A) = 4+1,1,8+2 = 0101,0001,1010 = (110011010)B
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
