四川省古蔺县中学校2012-2013学年高二下学期期中考试数学(文)试题
文档属性
| 名称 | 四川省古蔺县中学校2012-2013学年高二下学期期中考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 585.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-02 21:30:21 | ||
图片预览




文档简介
命题:杨 兵 审题:肖显彬 校对:杨斌
一、选择题(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若是虚数单位,则复数的值是( )
A. B. C. D.
2.“”是的( )
A.充分而不必要条件 B.必要不充分条件
C. 充要条件 D.既不充分也不必要条件
3. 已知命题,则是( )
A. B.
C. D.
4.双曲线的离心率为,则它的渐近线方程是( )
A. B. C. D.
5.函数,已知在时取得极值,则等于( )
A.2 B.3 C. 4 D.5
6.阅读如图所示的程序框图,运行相应的程序输出的结果是( )
A.3 B.11 C.38 D.123
7.曲线在点处的切线方程为 ( )
A. B.
C. D.
8. 直线 与圆交于E,F两点,则△EOF(O是原点)的面积为( )
A. B. C. D.
9.将一枚骰子抛掷两次,得到的点数分别为,那么点位于直线下方的概率为( )
A. B. C. D.
10.函数的大致图象如图所示,则等于
A. B. C. D.
二、填空题(本大题共5个小题,每小题5分,共25分,把答案填在答题卡规定的横线上)
11.已知,则=_____________
12. 如图,矩形中,点为边的中点,若在矩形内部随机取一个点,则点取自内部的概率等于_____________
13. 椭圆的一个顶点与两个焦点构成等边三角形,则离心率_____
14.已知命题“”为假命题,则的取值范围是_______
15.下列四个命题:
①命题“若,则“”的否命题是“若则”;
②若命题“”与命题“p或q”都是真命题,则命题q一定是真命题 ;
③“若,则有实根”的逆否命题是真命题;
④,,若是的必要不充分条件,则的取值范围是
其中正确命题的序号是___________________
三、解答题(本大题共6小题,共75分.解答时应写出必要的文字说明、证明过程或演算步聚)
16. (本题满分12分)
已知命题:方程的图象是焦点在轴上的双曲线;命题:命题:函数在上为单调递减;又为真,为假,求实数的取值范围.
17. (本题满分12分)
已知半径为的圆C的圆心在轴上,圆心的横坐标是整数,且与直线相切.
(1)求圆的方程;
(2)设直线与圆相交于,两点,求实数的取值范围.
18. (本题满分12分)
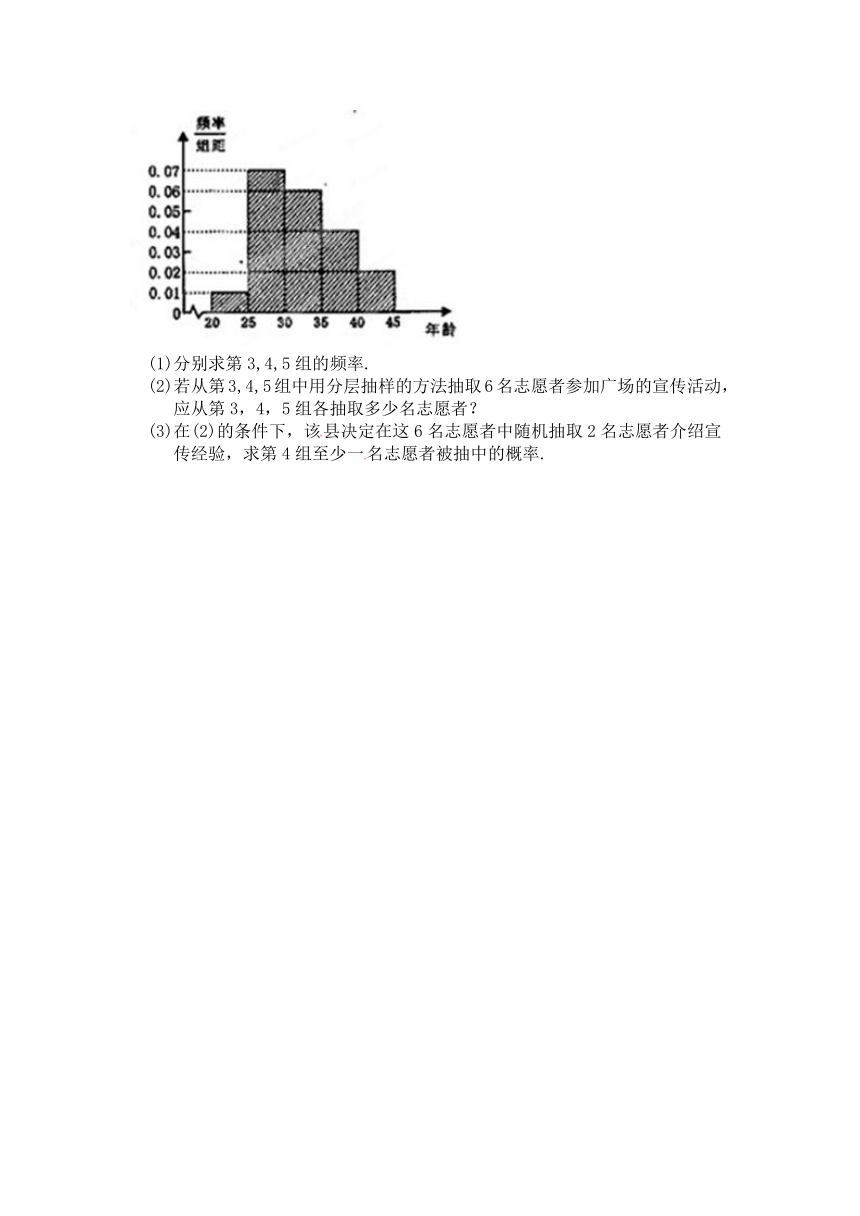
某县为增强市民的环保意识,面向全县征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示.
分别求第3,4,5组的频率.
若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
在(2)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少一名志愿者被抽中的概率. 19. (本小题12分)在直三棱柱中, ,
∠ACB=90°,M是 的中点,N是的中点
(Ⅰ)求证:MN∥平面 ;
(Ⅱ)求点到平面BMC的距离;
(Ⅲ)求二面角的平面角的余弦值大小。
20.(本小题满分13分)已知函数.
(1)时,求函数的单调区间.
(2)若在上单调递增,求实数的取值范围 .
21(本小题14分)已知椭圆:的离心率,直线与以原点为圆心,以椭圆的短半轴长为半径的圆相切.
(1)求椭圆的方程.
(2)设椭圆的的左焦点为,右焦点,直线过点且垂直于椭圆的长轴,动直线垂直于点,线段垂直平分线交于点,求点的轨迹的方程.
(3)设与轴交于点,不同的两点在上,且满足,求的取值范围.
古蔺中学高2011级2012-2013学年下期中考
数 学(文科) 试 题
题号
第I卷
第II卷
总分
二
三
得分
第Ⅰ卷选择题:(5×10=50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
第Ⅱ卷
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中横线上)
11、 12、
13、 14、
15、
三、解答题(本大题共6题,共75分,解答应写出文字说明,证明过程或演算步骤)
16. (12分)
17.(12分)
18.(12分)
19. (12分)
20.(13分)
21. (14分)
同课章节目录
