六年级上学期数学第三单元3.3整理和复习课件(共20张PPT)人教版
文档属性
| 名称 | 六年级上学期数学第三单元3.3整理和复习课件(共20张PPT)人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
整理和复习
回顾整理
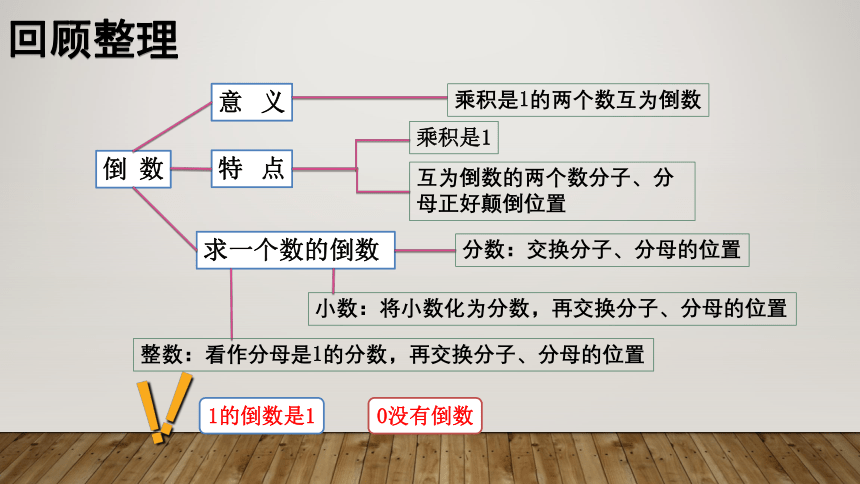
倒数
意义
乘积是1的两个数互为倒数
特点
乘积是1
互为倒数的两个数分子、分母正好颠倒位置
求一个数的倒数
分数:交换分子、分母的位置
小数:将小数化为分数,再交换分子、分母的位置
整数:看作分母是1的分数,再交换分子、分母的位置
1的倒数是1
0没有倒数
!
!
已知一个数的几分之几是多少,求这个数
已知比一个数多(或少)几分之几的数是多少,求这个数
工程类问题
分数除法
倒 数
解决问题
倒数的意义
求一个数的倒数的方法
分数除以整数
分数除法
一个数除以分数
分数混合运算
已知两个数的和(或差)及这两个数的倍数关系,求这两个数
校园里有柳树60棵_________,杨树有多少棵?
(2)柳树是杨树的 。
(1)杨树是柳树的 。
(3)杨树比柳树多 。
(4)柳树比杨树多 。
(6)柳树比杨树少 。
(5)杨树比柳树少 。
60×
60÷
60×(1+ )
60÷(1+ )
60×(1- )
60÷(1- )
六年级数学
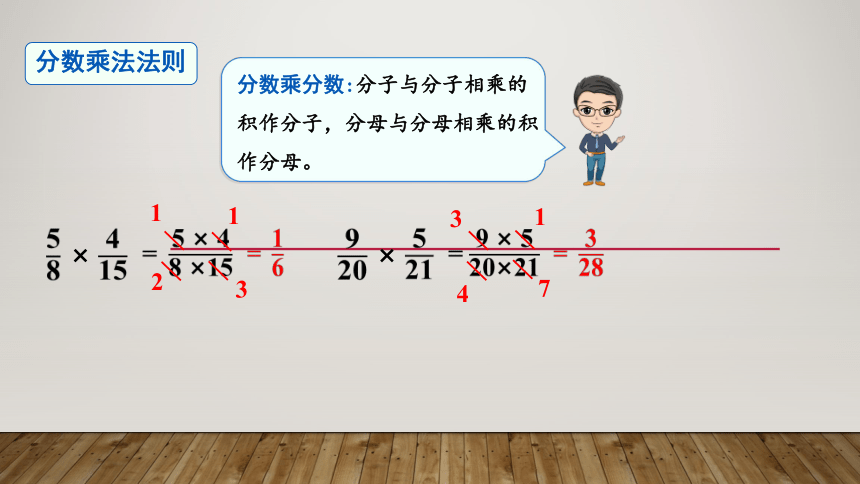
分数乘法法则
分数乘分数:分子与分子相乘的积作分子,分母与分母相乘的积作分母。
×
×
1
3
1
2
3
7
1
4
回顾分数除法的计算
计算下面各题
(1)
被除数不变,
除号变乘号,
除数变为它的倒数。
÷
= ×
=
1
3
1
5
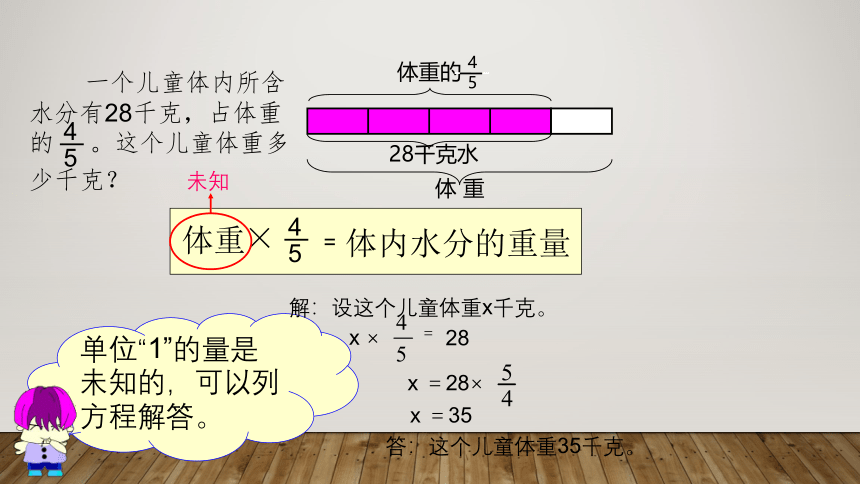
一个儿童体内所含水分有28千克,占体重的 。这个儿童体重多少千克?
4
5
体 重
28千克水
体重的
4
5
× =
体重
4
5
体内水分的重量
单位“1”的量是未知的,可以列方程解答。
未知
解:设这个儿童体重x千克。
x ×
=
28
x =28×
x =35
答:这个儿童体重35千克。
解分数除法应用题的一般步骤:
审题,找出已知和问题。
找准单位“1”。
画线段图。
列出数量关系式。
设未知数,列方程(或者列算式)。
求解,写答,检验。
÷13=
知识应用
整理和复习
1.计算下面各题。
15
16
÷5 =
3
16
12
25
12
325
13÷ =
45
65
4
13÷ =
2
17
221
2
21
40
÷ =
78
3
5
18
35
÷ × =
35
4
7
23
4
9
× ÷ =
15
16
1
2
56
7
24
÷ =
6
49
343
144
(13- )÷ =
35
186
7
7
15
35
64
÷( + )=
1
8
5
8
34
用分数除法解决工程类问题
用分数除法解决工程类实际问题的方法与用整数解决工程类实际问题的解题方法相同,所用的数量关系式也相同:“工作效率×工作时间=工作总量”、“工作总量÷工作效率=工作时间”、“工作总量÷工作时间=工作效率”。
用分数解决工程类实际问题时,把工作总量假设成“1”,用单位时间内完成工作总量的几分之一来表示工作效率。
过程
分数除法解决问题
阅读与理解
回顾与反思
分析与解答
条件、问题;有效信息
分析关键句
找等量关系
画线段图
检验
找准单位“1”对应关系
4.狮子奔跑时的最高时速可以达到60千米/时,比猎豹慢 。猎豹奔跑时的最高时速是多少?
5
11
已知比一个数少几分之几的数是多少,求这个数
答:猎豹奔跑时的最高时速是110千米/时。
解:设猎豹奔跑时的最高时速是 x 千米/时。
60÷(1- )
= 60÷
= 110(千米/时)
张大爷养的鹅和鸭共有700只,其中鹅的只数是鸭的 。鹅和鸭各有多少只?
【分析】题目中的等量关系式有:
鹅的只数+鸭的只数=700只
鹅的只数=鸭的只数×
一本故事书有120页,小明第一天读了全书的 ,第二天读了余下的 。
(1)第一天读了多少页?
(2)第二天读了多少页?
(3)第三天应从第几页读起?
现在的单价比原来降低了
小丽的体重比爸爸轻
一本书已经读了
六年级比五年级多捐
小结
今天你有什么收获?
复习整理的方法:不仅要关注学习的内容,还要关注知识之间的联系。
分数除法的计算方法可以用到所有除法运算中。
在解决问题时,学会找关系,多角度思考,灵活地解决问题
再见
整理和复习
回顾整理
倒数
意义
乘积是1的两个数互为倒数
特点
乘积是1
互为倒数的两个数分子、分母正好颠倒位置
求一个数的倒数
分数:交换分子、分母的位置
小数:将小数化为分数,再交换分子、分母的位置
整数:看作分母是1的分数,再交换分子、分母的位置
1的倒数是1
0没有倒数
!
!
已知一个数的几分之几是多少,求这个数
已知比一个数多(或少)几分之几的数是多少,求这个数
工程类问题
分数除法
倒 数
解决问题
倒数的意义
求一个数的倒数的方法
分数除以整数
分数除法
一个数除以分数
分数混合运算
已知两个数的和(或差)及这两个数的倍数关系,求这两个数
校园里有柳树60棵_________,杨树有多少棵?
(2)柳树是杨树的 。
(1)杨树是柳树的 。
(3)杨树比柳树多 。
(4)柳树比杨树多 。
(6)柳树比杨树少 。
(5)杨树比柳树少 。
60×
60÷
60×(1+ )
60÷(1+ )
60×(1- )
60÷(1- )
六年级数学
分数乘法法则
分数乘分数:分子与分子相乘的积作分子,分母与分母相乘的积作分母。
×
×
1
3
1
2
3
7
1
4
回顾分数除法的计算
计算下面各题
(1)
被除数不变,
除号变乘号,
除数变为它的倒数。
÷
= ×
=
1
3
1
5
一个儿童体内所含水分有28千克,占体重的 。这个儿童体重多少千克?
4
5
体 重
28千克水
体重的
4
5
× =
体重
4
5
体内水分的重量
单位“1”的量是未知的,可以列方程解答。
未知
解:设这个儿童体重x千克。
x ×
=
28
x =28×
x =35
答:这个儿童体重35千克。
解分数除法应用题的一般步骤:
审题,找出已知和问题。
找准单位“1”。
画线段图。
列出数量关系式。
设未知数,列方程(或者列算式)。
求解,写答,检验。
÷13=
知识应用
整理和复习
1.计算下面各题。
15
16
÷5 =
3
16
12
25
12
325
13÷ =
45
65
4
13÷ =
2
17
221
2
21
40
÷ =
78
3
5
18
35
÷ × =
35
4
7
23
4
9
× ÷ =
15
16
1
2
56
7
24
÷ =
6
49
343
144
(13- )÷ =
35
186
7
7
15
35
64
÷( + )=
1
8
5
8
34
用分数除法解决工程类问题
用分数除法解决工程类实际问题的方法与用整数解决工程类实际问题的解题方法相同,所用的数量关系式也相同:“工作效率×工作时间=工作总量”、“工作总量÷工作效率=工作时间”、“工作总量÷工作时间=工作效率”。
用分数解决工程类实际问题时,把工作总量假设成“1”,用单位时间内完成工作总量的几分之一来表示工作效率。
过程
分数除法解决问题
阅读与理解
回顾与反思
分析与解答
条件、问题;有效信息
分析关键句
找等量关系
画线段图
检验
找准单位“1”对应关系
4.狮子奔跑时的最高时速可以达到60千米/时,比猎豹慢 。猎豹奔跑时的最高时速是多少?
5
11
已知比一个数少几分之几的数是多少,求这个数
答:猎豹奔跑时的最高时速是110千米/时。
解:设猎豹奔跑时的最高时速是 x 千米/时。
60÷(1- )
= 60÷
= 110(千米/时)
张大爷养的鹅和鸭共有700只,其中鹅的只数是鸭的 。鹅和鸭各有多少只?
【分析】题目中的等量关系式有:
鹅的只数+鸭的只数=700只
鹅的只数=鸭的只数×
一本故事书有120页,小明第一天读了全书的 ,第二天读了余下的 。
(1)第一天读了多少页?
(2)第二天读了多少页?
(3)第三天应从第几页读起?
现在的单价比原来降低了
小丽的体重比爸爸轻
一本书已经读了
六年级比五年级多捐
小结
今天你有什么收获?
复习整理的方法:不仅要关注学习的内容,还要关注知识之间的联系。
分数除法的计算方法可以用到所有除法运算中。
在解决问题时,学会找关系,多角度思考,灵活地解决问题
再见
