沪科版八年级下册 19.1 多边形内角和课件(共15张PPT)
文档属性
| 名称 | 沪科版八年级下册 19.1 多边形内角和课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
19.1 多边形内角和
比
一
比
?
1、你能说一说什么叫三角形?
2、你能说出什么叫四边形、五边形、多边形吗?
由n条不在同一直线上的线段首尾顺次连结组成的平面图形,称为n边形.
又称为多边形.
探究新知
问题1:
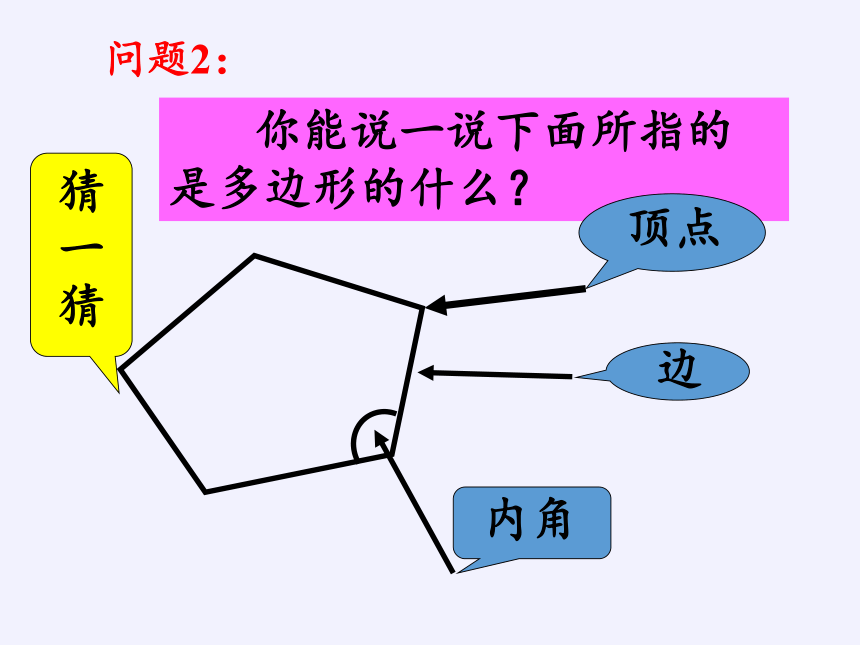
你能说一说下面所指的是多边形的什么?
猜一猜
边
内角
顶点
问题2:
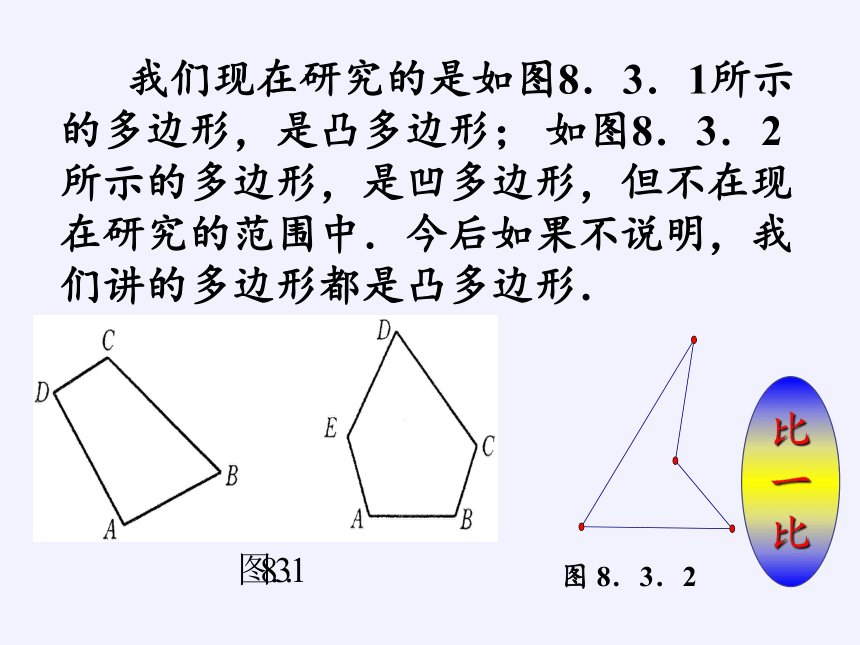
我们现在研究的是如图8.3.1所示的多边形,是凸多边形; 如图8.3.2所示的多边形,是凹多边形,但不在现在研究的范围中.今后如果不说明,我们讲的多边形都是凸多边形.
图 8.3.2
比
一
比
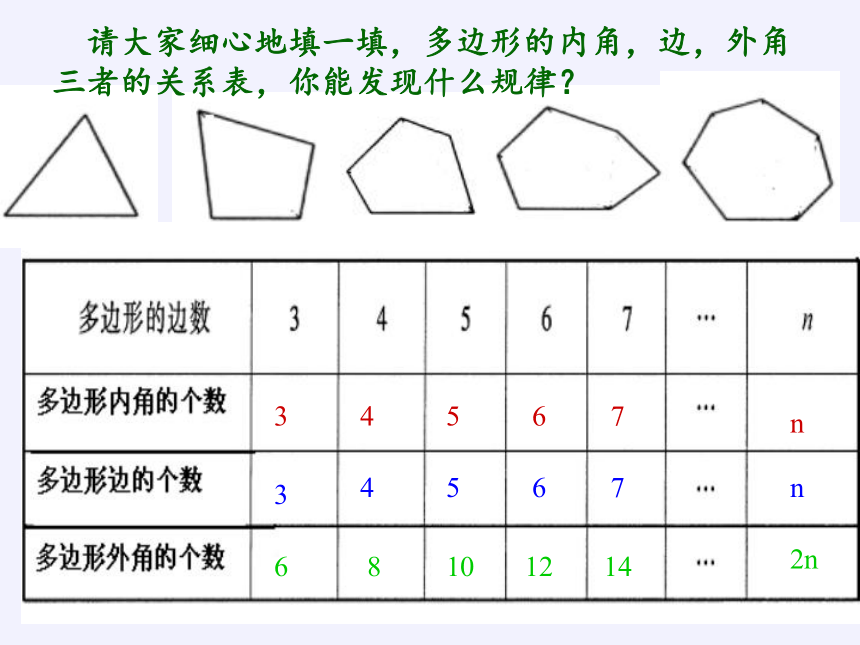
请大家细心地填一填,多边形的内角,边,外角三者的关系表,你能发现什么规律?
3
3
4
4
5
5
6
6
7
7
n
n
6
8
10
12
14
2n
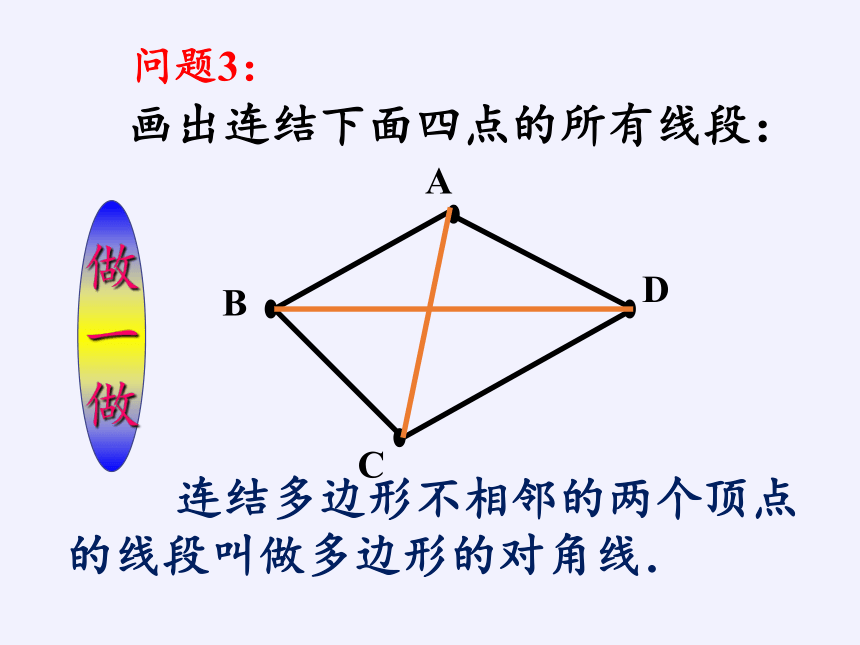
画出连结下面四点的所有线段:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
做
一
做
A
B
C
D
问题3:
四边形的内角和
A
D
C
B
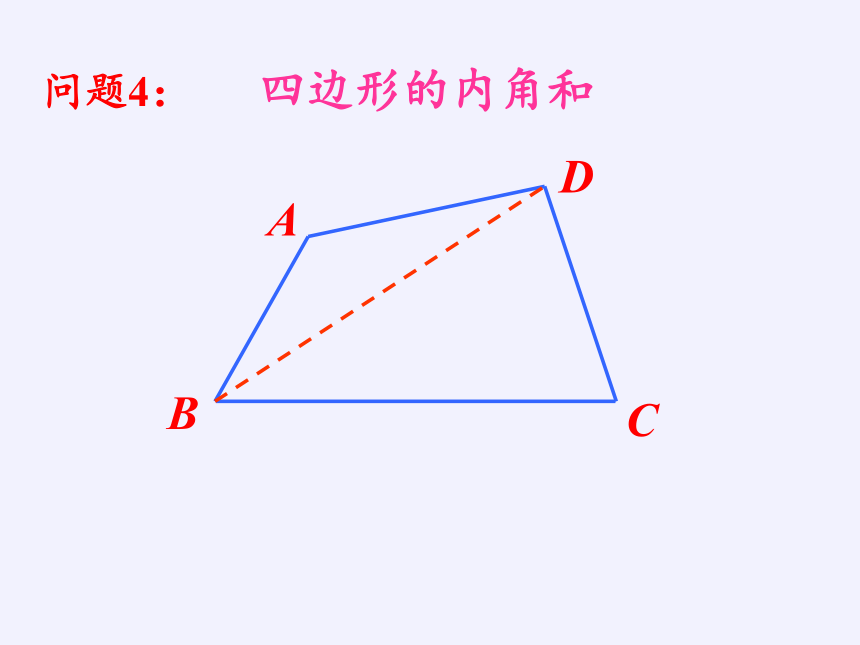
问题4:
四边形的内角和
A
D
C
B
结论:四边形的内角和为360o
∠A+∠B+∠C+∠D=360o
5边形
6边形
7边形
探究:多边形的内角和
对角线条数:
三角形个数:
内角和:
2
3
4
3
4
5
540°
720°
900°
…
n边形
?
?
?
问题5:
过多边形的一个顶点做对角线
n边形的内角和公式:
(n-2)×180°
结论:
那么对于正多边形来说,又遇到怎样的问题呢?
因为正多边形的每个角相等,所以知道正多
边形的边数,就可以求出每一个内角的度数.
(n-2)×180°/ n
例2
已知多边形的每一内角为150°,求这个多边形的边数.
解
设这个多边形的边数为n,
根据题意,得
(n-2)×180=150 n
解这个方程,得n= 12
经检验,符合题意
答:这个多边形的边数为12.
八边形的内角和是 ;
例1
1080o
应用公式解题:
四、课堂小结:
通过本节课的学习,谈谈你的收获、体会
应用新知
考考你
1.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
2.一个正方形瓷砖,截去一个角后:(1)还剩几个角?(2)剩下的多边形的内角和是多少度?
谢 谢
19.1 多边形内角和
比
一
比
?
1、你能说一说什么叫三角形?
2、你能说出什么叫四边形、五边形、多边形吗?
由n条不在同一直线上的线段首尾顺次连结组成的平面图形,称为n边形.
又称为多边形.
探究新知
问题1:
你能说一说下面所指的是多边形的什么?
猜一猜
边
内角
顶点
问题2:
我们现在研究的是如图8.3.1所示的多边形,是凸多边形; 如图8.3.2所示的多边形,是凹多边形,但不在现在研究的范围中.今后如果不说明,我们讲的多边形都是凸多边形.
图 8.3.2
比
一
比
请大家细心地填一填,多边形的内角,边,外角三者的关系表,你能发现什么规律?
3
3
4
4
5
5
6
6
7
7
n
n
6
8
10
12
14
2n
画出连结下面四点的所有线段:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
做
一
做
A
B
C
D
问题3:
四边形的内角和
A
D
C
B
问题4:
四边形的内角和
A
D
C
B
结论:四边形的内角和为360o
∠A+∠B+∠C+∠D=360o
5边形
6边形
7边形
探究:多边形的内角和
对角线条数:
三角形个数:
内角和:
2
3
4
3
4
5
540°
720°
900°
…
n边形
?
?
?
问题5:
过多边形的一个顶点做对角线
n边形的内角和公式:
(n-2)×180°
结论:
那么对于正多边形来说,又遇到怎样的问题呢?
因为正多边形的每个角相等,所以知道正多
边形的边数,就可以求出每一个内角的度数.
(n-2)×180°/ n
例2
已知多边形的每一内角为150°,求这个多边形的边数.
解
设这个多边形的边数为n,
根据题意,得
(n-2)×180=150 n
解这个方程,得n= 12
经检验,符合题意
答:这个多边形的边数为12.
八边形的内角和是 ;
例1
1080o
应用公式解题:
四、课堂小结:
通过本节课的学习,谈谈你的收获、体会
应用新知
考考你
1.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
2.一个正方形瓷砖,截去一个角后:(1)还剩几个角?(2)剩下的多边形的内角和是多少度?
谢 谢
