沪科版八年级下册 19.2平行四边形课件(共13张PPT)
文档属性
| 名称 | 沪科版八年级下册 19.2平行四边形课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 736.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 07:52:25 | ||
图片预览


文档简介
(共13张PPT)
2.平行四边形的性质:
1.两组对边分别 的四边形叫做平行四边形。
(1)平行四边形的对边
(2)平行四边形的对角
3.平行四边形性质的推论:
(1)夹在两条平行线间的平行线段
(2)平行线之间的距离
平行
相等
相等
相等
处处相等
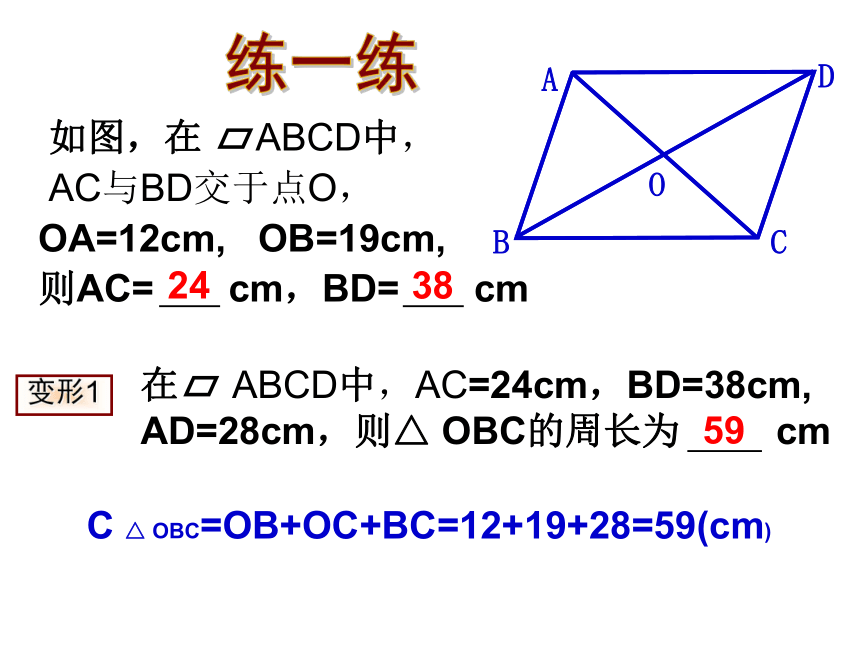
如图,在 ABCD中,
AC与BD交于点O,
OA=12cm, OB=19cm,
则AC= cm,BD= cm
C
B
O
D
A
24
38
在 ABCD中,AC=24cm,BD=38cm, AD=28cm,则△ OBC的周长为 cm
变形1
59
C △ OBC=OB+OC+BC=12+19+28=59(cm)
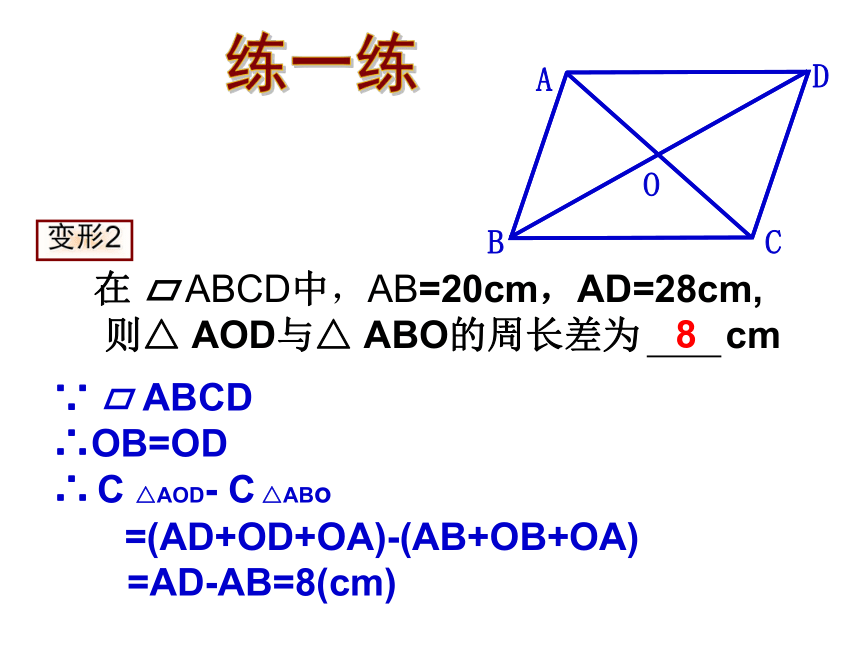
在 ABCD中,AB=20cm,AD=28cm,
则△ AOD与△ ABO的周长差为 cm
变形2
8
C
B
O
D
A
∵ ABCD
∴OB=OD
∴ C △AOD- C △ABo
=(AD+OD+OA)-(AB+OB+OA)
=AD-AB=8(cm)
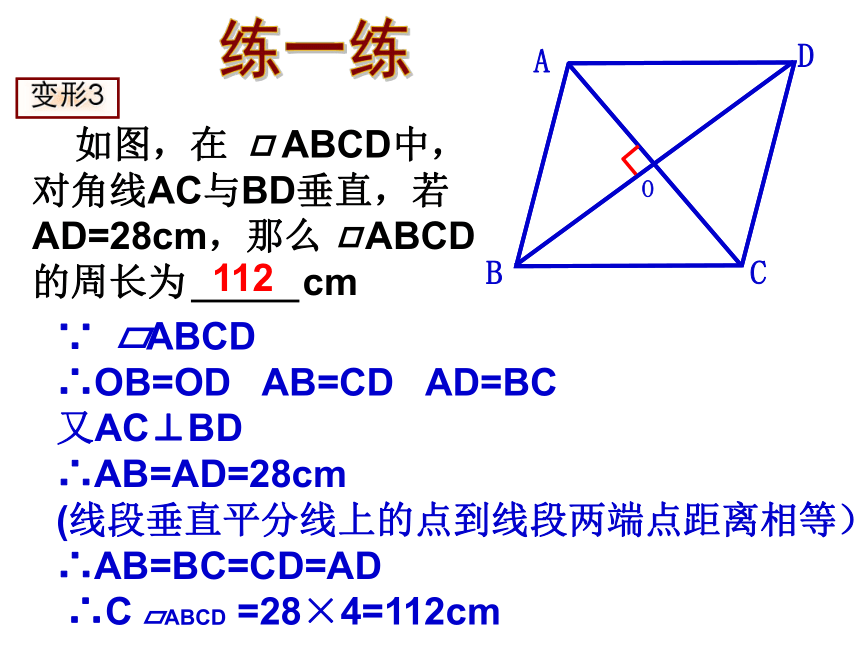
如图,在 ABCD中,对角线AC与BD垂直,若AD=28cm,那么 ABCD的周长为 cm
C
B
O
D
A
变形3
112
∵ ABCD
∴OB=OD AB=CD AD=BC
又AC⊥BD
∴AB=AD=28cm
(线段垂直平分线上的点到线段两端点距离相等)
∴AB=BC=CD=AD
∴C ABCD =28×4=112cm
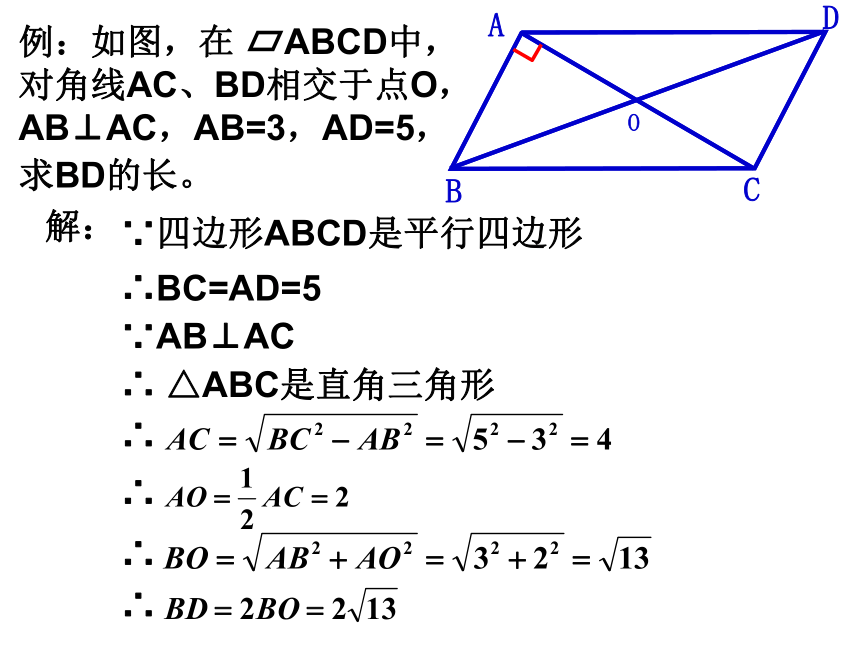
例:如图,在 ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,
求BD的长。
C
B
O
D
A
∵四边形ABCD是平行四边形
∴BC=AD=5
∵AB⊥AC
∴ △ABC是直角三角形
∴
∴
∴
解:
∴
ABCD的对角线AC与BD相交于O,直线EF过点O与AB 、CD分别相交于E 、F,试探究OE与OF的数量关系?并说明理由。
探 究
●
O
D
C
B
A
E
F
●
●
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下
图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
●
●
●
●
O
D
C
B
A
E
F
(1)
●
●
F
●
O
D
C
B
A
E
(2)
●
●
E
E
F
●
O
D
C
B
A
(3)
●
●
●
O
D
C
B
A
F
(4)
●
●
平行四边形
的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线
互相平分
2.平行四边形的性质:
1.两组对边分别 的四边形叫做平行四边形。
(1)平行四边形的对边
(2)平行四边形的对角
3.平行四边形性质的推论:
(1)夹在两条平行线间的平行线段
(2)平行线之间的距离
平行
相等
相等
相等
处处相等
如图,在 ABCD中,
AC与BD交于点O,
OA=12cm, OB=19cm,
则AC= cm,BD= cm
C
B
O
D
A
24
38
在 ABCD中,AC=24cm,BD=38cm, AD=28cm,则△ OBC的周长为 cm
变形1
59
C △ OBC=OB+OC+BC=12+19+28=59(cm)
在 ABCD中,AB=20cm,AD=28cm,
则△ AOD与△ ABO的周长差为 cm
变形2
8
C
B
O
D
A
∵ ABCD
∴OB=OD
∴ C △AOD- C △ABo
=(AD+OD+OA)-(AB+OB+OA)
=AD-AB=8(cm)
如图,在 ABCD中,对角线AC与BD垂直,若AD=28cm,那么 ABCD的周长为 cm
C
B
O
D
A
变形3
112
∵ ABCD
∴OB=OD AB=CD AD=BC
又AC⊥BD
∴AB=AD=28cm
(线段垂直平分线上的点到线段两端点距离相等)
∴AB=BC=CD=AD
∴C ABCD =28×4=112cm
例:如图,在 ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,
求BD的长。
C
B
O
D
A
∵四边形ABCD是平行四边形
∴BC=AD=5
∵AB⊥AC
∴ △ABC是直角三角形
∴
∴
∴
解:
∴
ABCD的对角线AC与BD相交于O,直线EF过点O与AB 、CD分别相交于E 、F,试探究OE与OF的数量关系?并说明理由。
探 究
●
O
D
C
B
A
E
F
●
●
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下
图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
●
●
●
●
O
D
C
B
A
E
F
(1)
●
●
F
●
O
D
C
B
A
E
(2)
●
●
E
E
F
●
O
D
C
B
A
(3)
●
●
●
O
D
C
B
A
F
(4)
●
●
平行四边形
的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线
互相平分
