《双减分层作业》第四章 三角形:回顾与思考(第一课时)含答案
文档属性
| 名称 | 《双减分层作业》第四章 三角形:回顾与思考(第一课时)含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 22:23:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 回顾与思考
(第一课时)
_____年_____月_____日
A基础达标:(完成时间__________分钟)
1、知识回顾与梳理:
1.三角形的角平分线:三角形一个内角的_________与这个角的对边相交,这个角的顶点和交点之间的___叫做三角形的角平分线.
2.三角形的中线:在三角形中,连接一个顶点和它的对边_________的___叫做三角形的中线.三角形的高线:从三角形的一个顶点向它的对边_______作垂线,顶点和垂足之间的___叫做三角形的高.
3.三角形的三条中线交于__点,这一点叫三角形的___.三角形的三条高所在的直线交于__点,三角形的三条角平分线交于_____点。
4.三角形三边的关系:三角形的任意两边之和____第三边,三角形任意两边之差_____第三边,三角形内角和定理:三角形内角和等于_____。
5.能够完全重合的两个三角形叫做________。
6.全等三角形的性质:__________________,_____________________。
7.三角形全等的判定方法有四种,分别是:____________________________。
二、基本题型训练:
(一)选择题:
1、下列长度的三条线段能组成三角形的是()
A.1,1,2 B.3,4,7 C.6,8,9 D.2,3,6
2、如图,在△ABC中,AC边上的高是()
A.线段AD B.线段BE C.线段BF D.线段CF
3、已知△ABC≌△DEF,,,则的度数为()
A. B. C.D.
4、小茜同学用三角形全等的知识测量A、B两点间的距离时,先在平面上选取一点C,可以直接到达点A、点B,且使BC⊥AB.再延长BC至点D,使CD=BC,过点D作DE⊥BC与AC的延长线交于点E,于是她测出DE的长为16 cm,便认为A、B两点间的距离为16 cm,小茜同学这样做的数学道理是( )
A.SSS B.SAS C.ASA D.以上都不对
5、已知a,b,c为三角形的三边,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是()
A.0 B.2a C.2a+2c D.2b﹣2c
(二)填空题:
6、在△ABC中,若∠B+∠A=∠C,则∠C=________
7、如图,在△ABC中,∠BAC=80°,∠C=45°,AD是△ABC的角平分线,那么∠ADB=_____度.
8、若长度分别为4,5,a的三条线段能组成一个三角形,则整数a的值可以是______.(写出一个即可)
9、若等腰三角形的两边长分别为3和7,则它的周长为_______; 若等腰三角形的两边长分别是3和4,则它的周长为_____.
10、在△ABC中,AD是中线,DE⊥AB,△ABC的面积为8,AB=4,则DE的长为 ___.
(三)解答题:
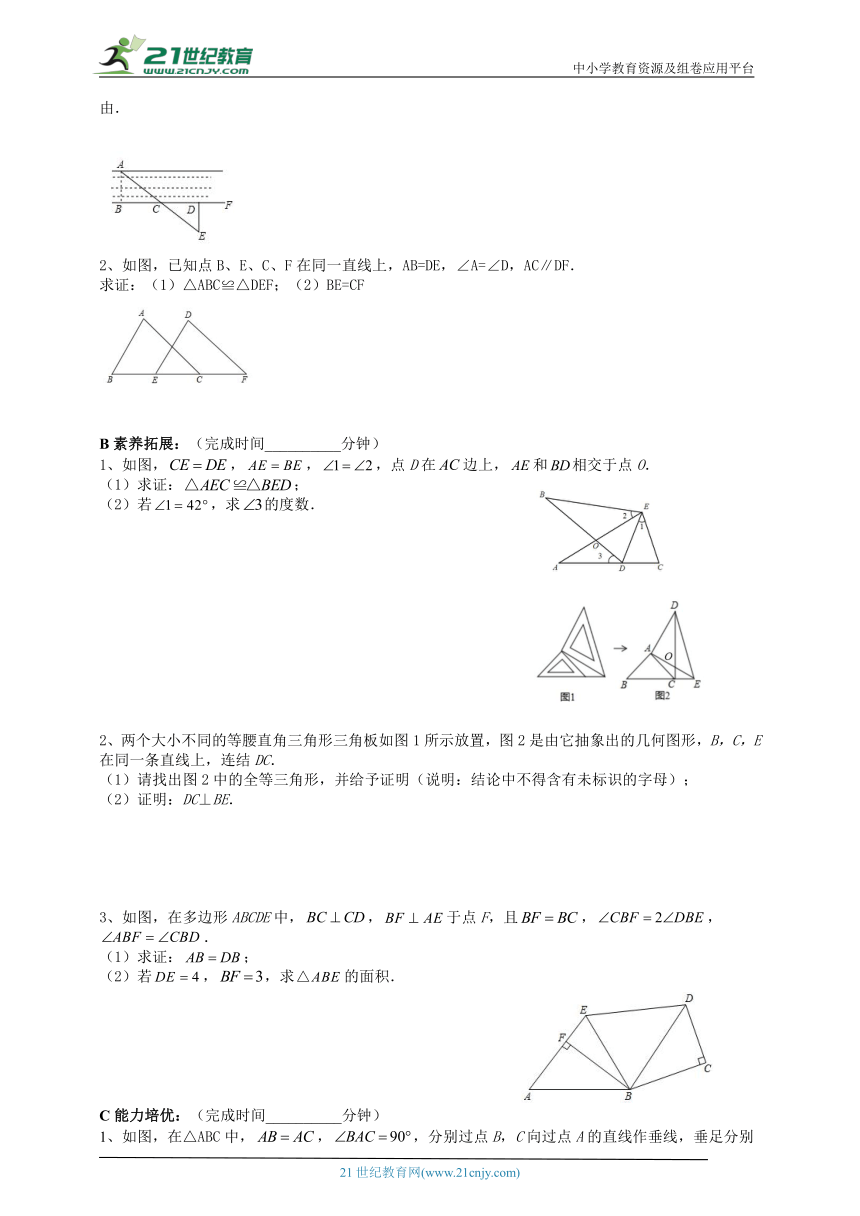
1、如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使过点D作,且A,C,E三点在一直线上.若测得米,即可知道AB也为15米.请说明理由.
2、如图,已知点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF;(2)BE=CF
B素养拓展:(完成时间__________分钟)
1、如图,,,,点D在边上,和相交于点O.
(1)求证:;
(2)若,求的度数.
2、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
3、如图,在多边形ABCDE中,,于点F,且,,.
(1)求证:;
(2)若,,求的面积.
C能力培优:(完成时间__________分钟)
1、如图,在△ABC中,,,分别过点B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图①,过点A的直线与斜边BC不相交时,求证:
①△ABE≌△CAF;
②.
(2)如图②,其他条件不变,过点A的直线与斜边BC相交时,若,,试求EF的长.
2、(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,直接写出△ABD与△CEF的面积之和.
第四章 回顾与思考(第一课时)参考答案
A:基础达标:(完成时间__________分钟)
知识回顾与梳理:1、角平分线 线段
2、 中点 线段 所在的直线 线段
3、一 重心 一 一
4、大于 小于 180°
5、全等三角形
6、对应边相等,对应角相等
7、SSS SAS ASA AAS
二、基本题型训练:
(一)选择题:
1.C 2.B 3.C 4.C 5.D
(二)填空题:
6.90° 7. 8.2 9.17 10或11 10.2
(三)解答题:
1.解:∵,,
∴,
在△ABC和△EDC中,
,
∴,
∴,
故AB也为15米.
2.证明:(1)∵AC∥DF
∴∠ACB=∠F
在△ABC与△DEF中
∴△ABC≌△DEF(AAS)
(2) ∵△ABC≌△DEF
∴BC=EF
∴BC–EC=EF–EC
即BE=CF
B:素养拓展:(完成时间__________分钟)
1.解:(1)证明:∵,
∴,
即.
在和△BED中,
,
∴
(2)∵,
∴.
∵,
∴.
2.解:(1)△ABE≌△ACD.
证明:∠BAC=∠EAD=90°,
∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
又AB=AC,AE=AD,
△ABE≌△ACD(SAS);
(2)由(1)得△ABE≌△ACD
∠ACD=∠B=45°
∠BCA=45°
∠BCD=∠BCA+∠ACD=90°,
DC⊥BE.
3.(1)∵,
∴∠BFA=∠C=90°
又,
∴△ABF≌△DBC,
∴;
(2)∵△ABF≌△DBC
∴∠ABF=∠DBC
∵===
∴∠ABE=∠DBE
又AB=DB,BE=BE
∴△ABE≌△DBE
∴AE=DE=4,
∴的面积为AE×BF=.
C:能力培优:(完成时间__________分钟)
1.(1)证明:①∵BE⊥EF,CF⊥EF,
∴∠AEB=∠CFA=90°,
∴∠EAB+∠EBA=90°,
∵∠BAC=90°,
∴∠EAB+∠FAC=90°,
∴∠EBA=∠FAC,
在△AEB与△CFA中
∵,
∴△ABE≌△CAF(AAS),
②∵△ABE≌△CAF,
∴EA=FC,EB=FA,
∴EF=AF+AE=BE+CF;
(2)解:∵BE⊥AF,CF⊥AF
∴∠AEB=∠CFA=90°
∴∠EAB+∠EBA=90°
∵∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC,
在△AEB与△CFA中
,
∴△ABE≌△CAF(AAS),
∴EA=FC,EB=FA,
∴EF=FA EA=EB FC=10 3=7.
2.(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2) 结论DE=BD+CE成立;
理由如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE
∴DE=AE+AD=BD+CE;
(3)△ABD与△CEF的面积之和为6.
∵∠BAD>∠CAE ,∠BDA=∠AEC=∠BAC
∴∠CAE=∠ABD
在△ABD和△CEA中
∴△ABD≌△CEA(AAS)
∴S△ABD=S△CEA
设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h.
∴S△ABC= BC h=12 ,S△ACF= CF h
∵BC=2CF
∴S△ACF=6
∴S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6
即△ABD与△CEF的面积之和为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第四章 回顾与思考
(第一课时)
_____年_____月_____日
A基础达标:(完成时间__________分钟)
1、知识回顾与梳理:
1.三角形的角平分线:三角形一个内角的_________与这个角的对边相交,这个角的顶点和交点之间的___叫做三角形的角平分线.
2.三角形的中线:在三角形中,连接一个顶点和它的对边_________的___叫做三角形的中线.三角形的高线:从三角形的一个顶点向它的对边_______作垂线,顶点和垂足之间的___叫做三角形的高.
3.三角形的三条中线交于__点,这一点叫三角形的___.三角形的三条高所在的直线交于__点,三角形的三条角平分线交于_____点。
4.三角形三边的关系:三角形的任意两边之和____第三边,三角形任意两边之差_____第三边,三角形内角和定理:三角形内角和等于_____。
5.能够完全重合的两个三角形叫做________。
6.全等三角形的性质:__________________,_____________________。
7.三角形全等的判定方法有四种,分别是:____________________________。
二、基本题型训练:
(一)选择题:
1、下列长度的三条线段能组成三角形的是()
A.1,1,2 B.3,4,7 C.6,8,9 D.2,3,6
2、如图,在△ABC中,AC边上的高是()
A.线段AD B.线段BE C.线段BF D.线段CF
3、已知△ABC≌△DEF,,,则的度数为()
A. B. C.D.
4、小茜同学用三角形全等的知识测量A、B两点间的距离时,先在平面上选取一点C,可以直接到达点A、点B,且使BC⊥AB.再延长BC至点D,使CD=BC,过点D作DE⊥BC与AC的延长线交于点E,于是她测出DE的长为16 cm,便认为A、B两点间的距离为16 cm,小茜同学这样做的数学道理是( )
A.SSS B.SAS C.ASA D.以上都不对
5、已知a,b,c为三角形的三边,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是()
A.0 B.2a C.2a+2c D.2b﹣2c
(二)填空题:
6、在△ABC中,若∠B+∠A=∠C,则∠C=________
7、如图,在△ABC中,∠BAC=80°,∠C=45°,AD是△ABC的角平分线,那么∠ADB=_____度.
8、若长度分别为4,5,a的三条线段能组成一个三角形,则整数a的值可以是______.(写出一个即可)
9、若等腰三角形的两边长分别为3和7,则它的周长为_______; 若等腰三角形的两边长分别是3和4,则它的周长为_____.
10、在△ABC中,AD是中线,DE⊥AB,△ABC的面积为8,AB=4,则DE的长为 ___.
(三)解答题:
1、如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使过点D作,且A,C,E三点在一直线上.若测得米,即可知道AB也为15米.请说明理由.
2、如图,已知点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF;(2)BE=CF
B素养拓展:(完成时间__________分钟)
1、如图,,,,点D在边上,和相交于点O.
(1)求证:;
(2)若,求的度数.
2、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
3、如图,在多边形ABCDE中,,于点F,且,,.
(1)求证:;
(2)若,,求的面积.
C能力培优:(完成时间__________分钟)
1、如图,在△ABC中,,,分别过点B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图①,过点A的直线与斜边BC不相交时,求证:
①△ABE≌△CAF;
②.
(2)如图②,其他条件不变,过点A的直线与斜边BC相交时,若,,试求EF的长.
2、(1)如图①,已知:Rt△ABC中,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:△ABC中,AB=AC,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,直接写出△ABD与△CEF的面积之和.
第四章 回顾与思考(第一课时)参考答案
A:基础达标:(完成时间__________分钟)
知识回顾与梳理:1、角平分线 线段
2、 中点 线段 所在的直线 线段
3、一 重心 一 一
4、大于 小于 180°
5、全等三角形
6、对应边相等,对应角相等
7、SSS SAS ASA AAS
二、基本题型训练:
(一)选择题:
1.C 2.B 3.C 4.C 5.D
(二)填空题:
6.90° 7. 8.2 9.17 10或11 10.2
(三)解答题:
1.解:∵,,
∴,
在△ABC和△EDC中,
,
∴,
∴,
故AB也为15米.
2.证明:(1)∵AC∥DF
∴∠ACB=∠F
在△ABC与△DEF中
∴△ABC≌△DEF(AAS)
(2) ∵△ABC≌△DEF
∴BC=EF
∴BC–EC=EF–EC
即BE=CF
B:素养拓展:(完成时间__________分钟)
1.解:(1)证明:∵,
∴,
即.
在和△BED中,
,
∴
(2)∵,
∴.
∵,
∴.
2.解:(1)△ABE≌△ACD.
证明:∠BAC=∠EAD=90°,
∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
又AB=AC,AE=AD,
△ABE≌△ACD(SAS);
(2)由(1)得△ABE≌△ACD
∠ACD=∠B=45°
∠BCA=45°
∠BCD=∠BCA+∠ACD=90°,
DC⊥BE.
3.(1)∵,
∴∠BFA=∠C=90°
又,
∴△ABF≌△DBC,
∴;
(2)∵△ABF≌△DBC
∴∠ABF=∠DBC
∵===
∴∠ABE=∠DBE
又AB=DB,BE=BE
∴△ABE≌△DBE
∴AE=DE=4,
∴的面积为AE×BF=.
C:能力培优:(完成时间__________分钟)
1.(1)证明:①∵BE⊥EF,CF⊥EF,
∴∠AEB=∠CFA=90°,
∴∠EAB+∠EBA=90°,
∵∠BAC=90°,
∴∠EAB+∠FAC=90°,
∴∠EBA=∠FAC,
在△AEB与△CFA中
∵,
∴△ABE≌△CAF(AAS),
②∵△ABE≌△CAF,
∴EA=FC,EB=FA,
∴EF=AF+AE=BE+CF;
(2)解:∵BE⊥AF,CF⊥AF
∴∠AEB=∠CFA=90°
∴∠EAB+∠EBA=90°
∵∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC,
在△AEB与△CFA中
,
∴△ABE≌△CAF(AAS),
∴EA=FC,EB=FA,
∴EF=FA EA=EB FC=10 3=7.
2.(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2) 结论DE=BD+CE成立;
理由如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE
∴DE=AE+AD=BD+CE;
(3)△ABD与△CEF的面积之和为6.
∵∠BAD>∠CAE ,∠BDA=∠AEC=∠BAC
∴∠CAE=∠ABD
在△ABD和△CEA中
∴△ABD≌△CEA(AAS)
∴S△ABD=S△CEA
设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h.
∴S△ABC= BC h=12 ,S△ACF= CF h
∵BC=2CF
∴S△ACF=6
∴S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6
即△ABD与△CEF的面积之和为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
