小学数学苏教版六年级下7.1.14 正比例和反比例 课件(共16张PPT)
文档属性
| 名称 | 小学数学苏教版六年级下7.1.14 正比例和反比例 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 21:23:10 | ||
图片预览





文档简介
(共16张PPT)
1. 举例说明什么叫做正比例?
2.举例说明什么叫做反比例
3.正比例和反比例有什么相同点和不同点?
4.你是怎样判断两种相关联的量成什么比例
5.生活中成正比例或反比例量的例子。
正比例关系是什么?举例说明。
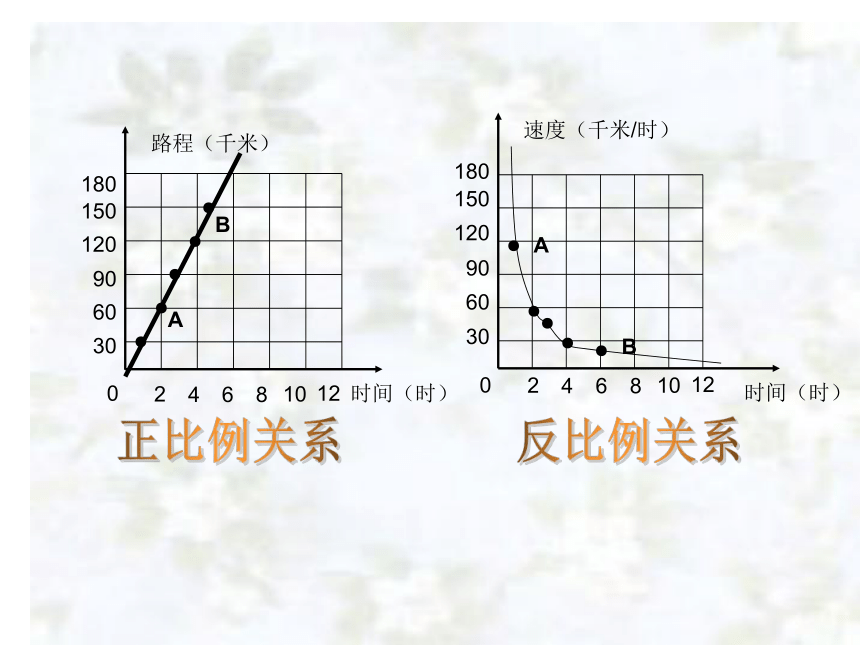
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。如,当速度一定时,路程与时间这两种量成正比例关系。
反比例关系是什么?举例说明。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。如,当路程一定时,速度与时间这两种量成反比例关系。
名称
正比例
反比例
联系
两种相关联的量,一种量变化,另一种量也随着变化。
区别
特征
关系式
相对应的两个数的比值(商)一定。
相对应的两个数的积一定。
Xy=k
(一定)
0
2
4
6
8
10
12
150
30
60
90
120
180
路程(千米)
时间(时)
●
●
●
●
●
2
4
6
8
10
12
0
150
30
60
90
120
180
速度(千米/时)
时间(时)
●
●
●
●
●
A
B
A
B
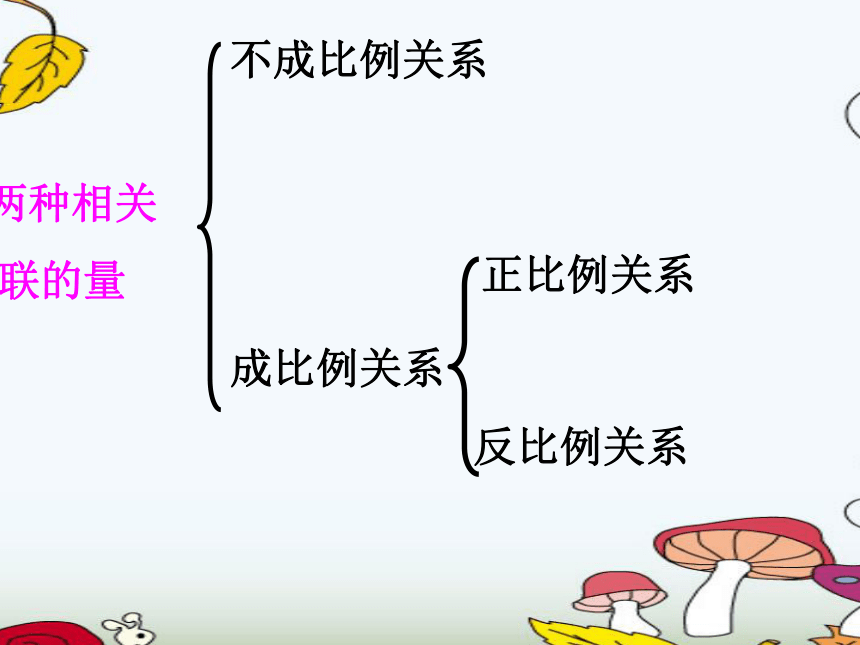
两种相关
联的量
不成比例关系
成比例关系
正比例关系
反比例关系
一看:首先要看这两种量是不是相关联的量,一种量是不是随着另一种量的变化而变化 ;
二列:列出数量间的相等关系;
三找:找出谁是不变的量;
四判断: 商一定,两种量成正比例; 积一定,两种量成反比例。
(1)收入一定,支出和结余成正比例。( )
(2)出米率一定,稻谷的重量和大米的重量成正比例。( )
(3)圆柱的侧面 积一定,它的底面周长和高成正比例。( )
(4)在一定时间内,生产一个零件所用的时间和零件个数成正比例。( )
(5)三角形的面积一定,它的底和高成反比例。( )
(6)小明从家步行到学校,步行 的速度和所需的时间成反比例。( )
木料总量、每件家具的用料和制成家具的件数这三种量:
1、当( )一定时,( )和( )成反比例。
2、当( )一定时,( )和( )成正比例。
3、当 ( )一定时,( )和( )成正比例。
木料总量
每件家具的用料
制成家具的件数
每件家具的用料
木料总量
制成家具的件数
制成家具的件数
木料总量
每件家具的用料
正
正
反
(1)在一幅地图上,比例尺一定,实际距离和图上距离( )。
A、成正比例 B、不成比例 C、成反比例
A
(2)与圆的面积成正比例的是( )。
A、半径 B、直径 C、半径的平方
C
(3)路程一定,车轮的半径和转数( )。
A、成正比例 B、不成比例 C、成反比例
C
(4)砖块的面积一定,铺地的面积和用砖的块数( )。
A、成正比例 B、不成比C、成反比例
(5)正方体一个面的面积和它的表面积( )。
A、成正比例 B、不成比例 C、成反比例
A
A
判断下面每题中的两种量是不是成比例,成什么比例?并说明理由。
1. 每包书中册数相同,包数和总册数。
2. 被除数一定,除数和商。
3. 全班的学生人数一定,每组的人数和组数。
4. 圆的面积与半径。
5. 房间地面面积一定,房间里的人数和每人
所占的面积。
6. 和一定,加数和另一个加数。
7. 一个人的年龄和他的体重。
1、同学们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?
2.张明骑摩托3小时行了150千米,照这样的速度,从家到街上行了1.2小时,张明家到街上有多远?
20×18=360(人) 360÷24=15(行)
答:
150÷3=50(千米 ) 50 ×1.2=60(千米)
答:….
数学与生活
1. 举例说明什么叫做正比例?
2.举例说明什么叫做反比例
3.正比例和反比例有什么相同点和不同点?
4.你是怎样判断两种相关联的量成什么比例
5.生活中成正比例或反比例量的例子。
正比例关系是什么?举例说明。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。如,当速度一定时,路程与时间这两种量成正比例关系。
反比例关系是什么?举例说明。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。如,当路程一定时,速度与时间这两种量成反比例关系。
名称
正比例
反比例
联系
两种相关联的量,一种量变化,另一种量也随着变化。
区别
特征
关系式
相对应的两个数的比值(商)一定。
相对应的两个数的积一定。
Xy=k
(一定)
0
2
4
6
8
10
12
150
30
60
90
120
180
路程(千米)
时间(时)
●
●
●
●
●
2
4
6
8
10
12
0
150
30
60
90
120
180
速度(千米/时)
时间(时)
●
●
●
●
●
A
B
A
B
两种相关
联的量
不成比例关系
成比例关系
正比例关系
反比例关系
一看:首先要看这两种量是不是相关联的量,一种量是不是随着另一种量的变化而变化 ;
二列:列出数量间的相等关系;
三找:找出谁是不变的量;
四判断: 商一定,两种量成正比例; 积一定,两种量成反比例。
(1)收入一定,支出和结余成正比例。( )
(2)出米率一定,稻谷的重量和大米的重量成正比例。( )
(3)圆柱的侧面 积一定,它的底面周长和高成正比例。( )
(4)在一定时间内,生产一个零件所用的时间和零件个数成正比例。( )
(5)三角形的面积一定,它的底和高成反比例。( )
(6)小明从家步行到学校,步行 的速度和所需的时间成反比例。( )
木料总量、每件家具的用料和制成家具的件数这三种量:
1、当( )一定时,( )和( )成反比例。
2、当( )一定时,( )和( )成正比例。
3、当 ( )一定时,( )和( )成正比例。
木料总量
每件家具的用料
制成家具的件数
每件家具的用料
木料总量
制成家具的件数
制成家具的件数
木料总量
每件家具的用料
正
正
反
(1)在一幅地图上,比例尺一定,实际距离和图上距离( )。
A、成正比例 B、不成比例 C、成反比例
A
(2)与圆的面积成正比例的是( )。
A、半径 B、直径 C、半径的平方
C
(3)路程一定,车轮的半径和转数( )。
A、成正比例 B、不成比例 C、成反比例
C
(4)砖块的面积一定,铺地的面积和用砖的块数( )。
A、成正比例 B、不成比C、成反比例
(5)正方体一个面的面积和它的表面积( )。
A、成正比例 B、不成比例 C、成反比例
A
A
判断下面每题中的两种量是不是成比例,成什么比例?并说明理由。
1. 每包书中册数相同,包数和总册数。
2. 被除数一定,除数和商。
3. 全班的学生人数一定,每组的人数和组数。
4. 圆的面积与半径。
5. 房间地面面积一定,房间里的人数和每人
所占的面积。
6. 和一定,加数和另一个加数。
7. 一个人的年龄和他的体重。
1、同学们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?
2.张明骑摩托3小时行了150千米,照这样的速度,从家到街上行了1.2小时,张明家到街上有多远?
20×18=360(人) 360÷24=15(行)
答:
150÷3=50(千米 ) 50 ×1.2=60(千米)
答:….
数学与生活
