8.2立体图形的直观图课件——2021-2022学年高一下学期数学人教A版(2019)必修第二册(共30张PPT)
文档属性
| 名称 | 8.2立体图形的直观图课件——2021-2022学年高一下学期数学人教A版(2019)必修第二册(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 09:16:14 | ||
图片预览





文档简介
(共30张PPT)
8.2 立体图形的直观图
人教A版2019高中数学必修第二册
第八章 立体几何初步
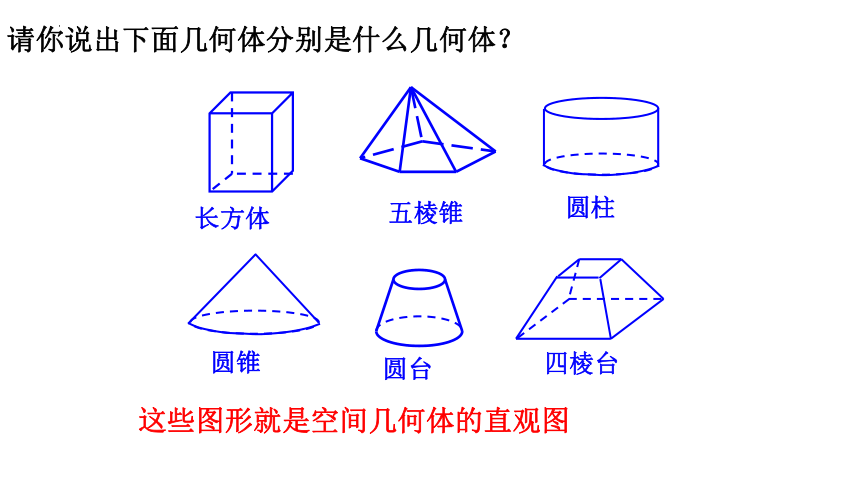
请你说出下面几何体分别是什么几何体?
长方体
五棱锥
圆柱
圆锥
圆台
四棱台
这些图形就是空间几何体的直观图
直观图是观察者站在某一点观察一个空间几何体获得的图形。
画立体图形的直观图,实际上是把不完全在同一平面内的点的集合,用同一平面内的点表示。
因此,直观图往往与立体图形的真实形状不完全相同,在立体几何中,立体图形的直观图通常是在平行投影下得到的平面图形。
要画立体图形的直观图,首先要学会画水平放置的平面图形。
观察:如图,矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状?
利用平行投影,人们获得了画直观图的斜二测画法.
下面我们来学习利用这种画法画水平放置的平面图形的直观图.
都是平行四边形
A
B
C
D
y
x
O
y′
x′
O′
D′
C′
B′
A′
用斜二测画法画水平放置的平面图形的直观图的步骤
x不变,y折半
x′
y′
O′
x
y
O
D
A
C
B
D’
A’
C’
B’
M
N
M’
N’
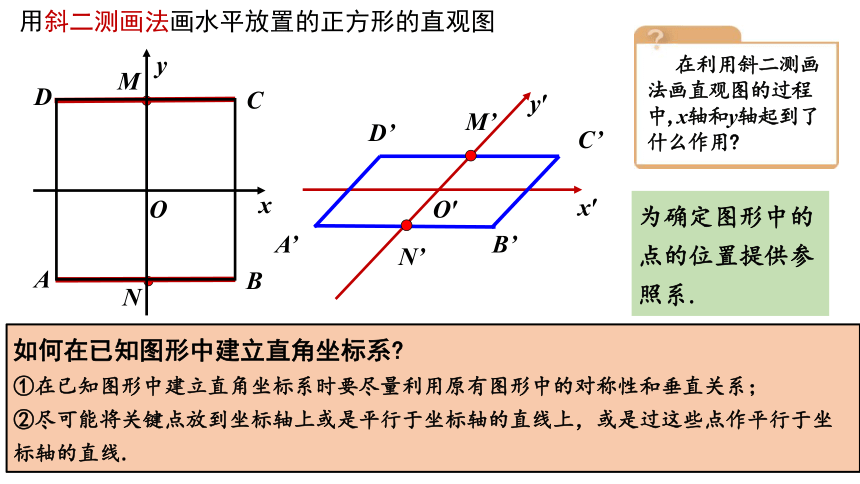
用斜二测画法画水平放置的正方形的直观图
如何在已知图形中建立直角坐标系
①在已知图形中建立直角坐标系时要尽量利用原有图形中的对称性和垂直关系;
②尽可能将关键点放到坐标轴上或是平行于坐标轴的直线上,或是过这些点作平行于坐标轴的直线.
在利用斜二测画法画直观图的过程中,x轴和y轴起到了什么作用
为确定图形中的点的位置提供参照系.
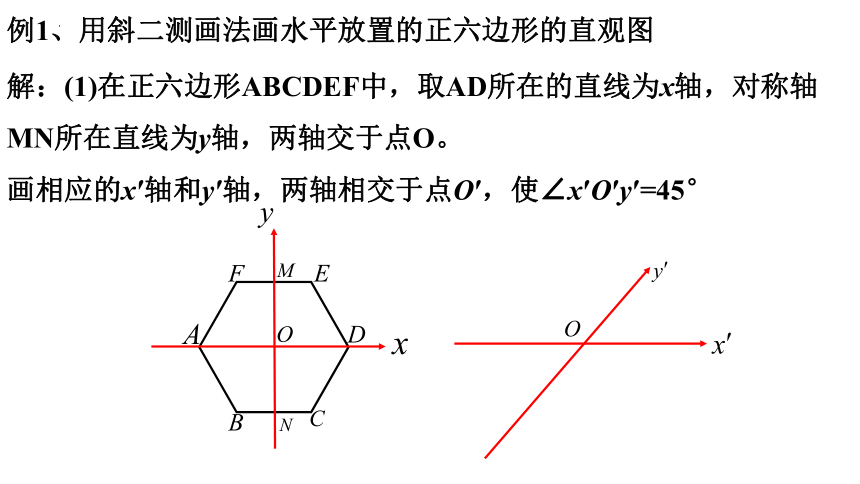
例1、用斜二测画法画水平放置的正六边形的直观图
解:(1)在正六边形ABCDEF中,取AD所在的直线为x轴,对称轴MN所在直线为y轴,两轴交于点O。
画相应的x′轴和y′轴,两轴相交于点O′,使∠x′O′y′=45°
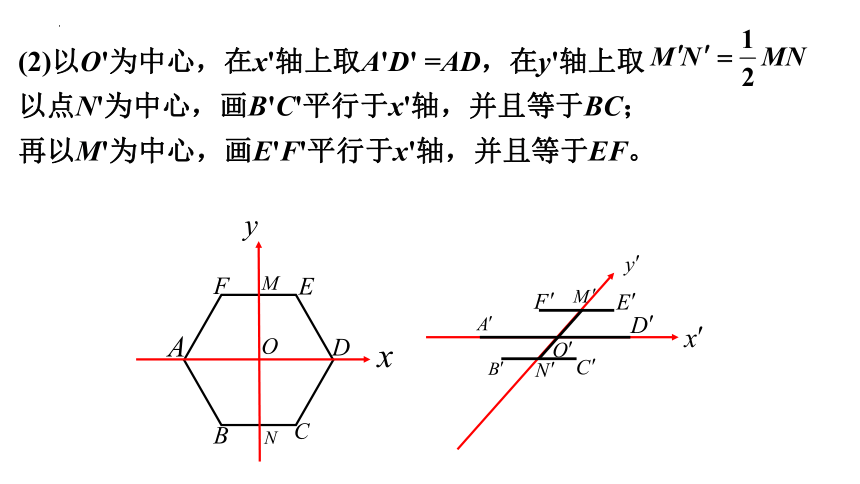
(2)以O'为中心,在x'轴上取A'D' =AD,在y'轴上取
以点N'为中心,画B'C'平行于x'轴,并且等于BC;
再以M'为中心,画E'F'平行于x'轴,并且等于EF。
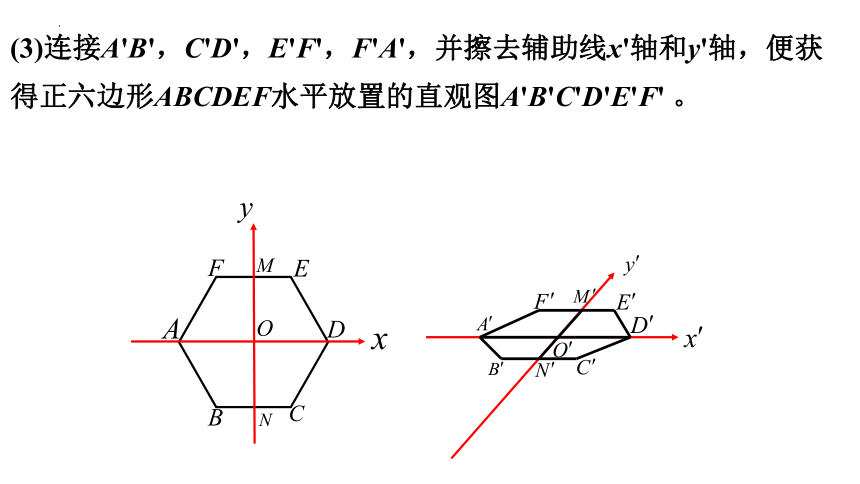
(3)连接A'B',C'D',E'F',F'A',并擦去辅助线x'轴和y'轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 。
①斜二测画法中,“斜”是指把直角坐标系xOy变为斜坐标系x'O'y',使∠x'O'y'=45 (或135 ),“二测”是指画直观图时,平行于x轴的线段长度不变,平行于y轴的线段长度减半.
②画平面图形的直观图,首先画与坐标轴平行的线段(平行性不变),对于与坐标轴不平行的线段,通过与坐标轴平行的线段确定它的两个端点,然后连接成线段.
斜二测画法画平面图形的直观图的剖析
③斜二测画法的位置特征与度量特征简记为:
x不变,y折半。
平行关系不改变
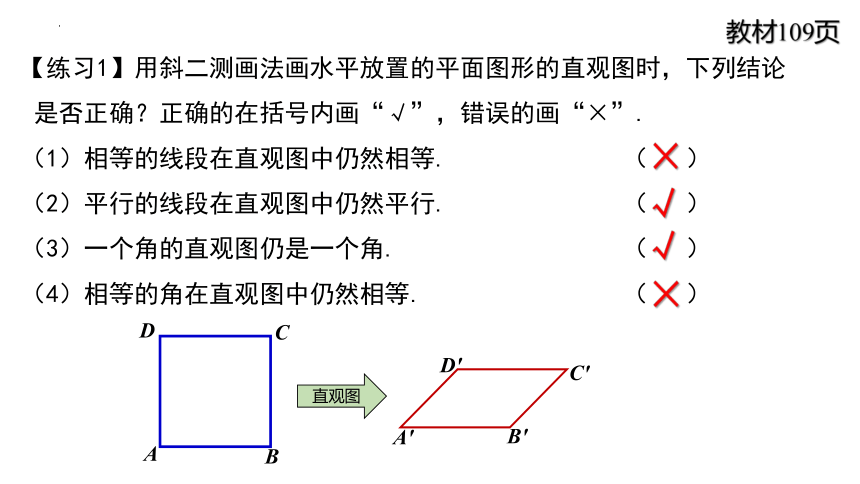
【练习1】用斜二测画法画水平放置的平面图形的直观图时,下列结论
是否正确?正确的在括号内画“√”,错误的画“×”.
(1)相等的线段在直观图中仍然相等. ( )
(2)平行的线段在直观图中仍然平行. ( )
(3)一个角的直观图仍是一个角. ( )
(4)相等的角在直观图中仍然相等. ( )
√
√
×
×
A
B
C
D
直观图
A′
B′
C′
D′
教材109页
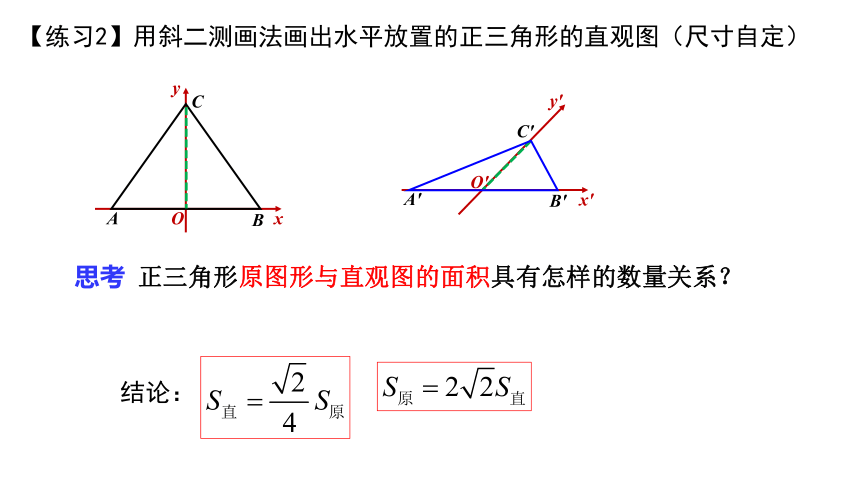
【练习2】用斜二测画法画出水平放置的正三角形的直观图(尺寸自定)
y
x
O
A
B
C
y′
x′
O′
A′
B′
C′
思考 正三角形原图形与直观图的面积具有怎样的数量关系?
结论:
【练习】如图,已知ABC的直观图为A'B'C',若A'C'=A'B'=3,则ABC的面积为___________.
y′
x′
O′
C′
B′
(A′)
9
生活经验告诉我们,水平放置的圆看起来非常像椭圆,立体几何中,我们常用正等测画法画水平放置的圆,在实际画水平放置的圆的直观图时常用下图所示的椭圆模板。
水平放置的圆给我们的视觉效果是什么图形呢?
画几何体的直观图时,一般先使用平面图形的斜二测画法画几何体的底面,这时与画平面图形的直观图相比,只要多画了一个与x轴、y轴都垂直的z轴,并且使平行于z轴的线段的平行性和长度都不变.
下面介绍几种简单几何体的直观图的画法.
x
y
o
z
x
y
o
【例2】已知长方体ABCD-A′B′C′D′的长、宽、高分别为3cm、2cm、1.5cm,
用斜二测画法画出它的直观图.
A
B
C
D
z
[画法]
(1)画轴.
如图,画x轴、y轴、z 轴,三轴相交于点 O(A),使∠xOy=45°,∠xOz=90°.
(2)画底面.
在x轴正半轴上取线段 AB,使AB=3 cm;在y轴正半轴上取线段 AD,使AD=1 cm.
过点B作y轴的平行线,过点D作x轴的平行线,设它们的交点为C,
则□ABCD就是长方体的底面ABCD的直观图.
x
y
o
【例2】已知长方体的长、宽、高ABCD-A′B′C′D′分别为3cm、2cm、1.5cm,
用斜二测画法画出它的直观图.
A
B
C
D
z
A′
B′
C′
D′
A′
B′
C′
D′
A
B
C
D
(3)画侧棱. 在z轴正半轴上取线段AA',使AA'=1.5 cm,过B,C,D各点分别作z 轴平行线,在这些平行线上分别截取1.5 cm长的线段 BB',CC',DD'.
(4)成图.顺次连接A′,B',C',D',并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图了.
练习 棱柱的画法:请画出底面边长为1,高为3的正六棱柱的直观图.
x'
y'
O'
z'
B'
C'
D'
E'
F'
A'
B
C
D
E
F
A
H'
G'
b
a
A
B
C
D
E
F
O
(1)在已知空间几何体中取水平平面,在水平平面内取互相垂直的x轴和y轴,两轴相交于点O.过点O取与x轴、y轴都垂直的z轴. 画直观图时,把它们画成对应的x'轴、y'轴和z'轴,三轴相交于点O',且使∠x'O'y'=45 (或135 ),∠x'O'z'=90 ,x'轴与y'轴所确定的平面表示水平面.
(3)已知几何体中平行于x轴或z轴的线段,在直观图中保持原长度不变,平行于y轴的线段,在直观图中长度为原来的一半.
(2)已知几何体中平行于x轴、y轴或z轴的线段,在直观图中分别画成平行于x'轴、y'轴或z'轴的线段.
4.斜二测画法画空间几何体的直观图的步骤
(4)连线成图以后,擦掉作为辅助线的坐标轴,将被遮挡的部分改为虚线,就得到了空间几何体的直观图.
①画空间几何体的直观图在要求不太严格的情况下,长度和角度可适当选取.为了增强立体感,被挡住的部分通常用虚线表示.
②斜二测画法保持了原图形的平行性、共线性,保持了平行线段的长度比.
斜二测画法画空间几何体的直观图的剖析
③坐标系的建立要充分利用几何体的对称性,坐标原点一般建在图形的对称中心处,使几何体的顶点尽可能多地落在坐标轴上.
④要先画出底面的直观图,再画出其余各面.
【例3】已知圆柱底面半径为1cm,侧面母线长3cm,画出它的直观图.
解:(1)画轴.如图,画x轴,z轴,使∠xOz=90°.
(2)画下底面. 以O为中点,在x轴上取线段AB,使OA=OB=1cm. 利用椭圆模板画椭圆,使其经过A、B两点. 这个椭圆就是圆柱的下底面.
(3)画上底面. 在Oz上截取O',使OO'=3cm. 过点O'作平行于轴Ox的轴O'x'. 类似下底面的作法作出圆柱的上底面.
(4)成图. 连接AA',BB',整理得到圆柱的直观图.
O
圆锥
O
球
对于圆锥的直观图,一般先画圆锥的底面,再借助于圆锥的轴确定圆锥的顶点,最后画出两侧的两条母线.
画球的直观图,一般需要画出球的轮廓线,它是一个圆.同时还经常画出经过球心的截面圆,它们的直观图是椭圆,用以衬托球的立体性.
O
球
【例4】某简单组合体由上下两部分组成,下部是一个圆柱,上部是一个圆锥,圆锥的底面与圆柱的上底面重合.画出这个组合体的直观图.
解:画法:如图,先画出圆柱的上下底面,再在圆柱和圆锥共同的轴线上确定圆锥的顶点,最后画出圆柱和圆锥的母线,并标注相关字母,就得到组合体的直观图.
2、空间几何体直观图斜二测画法步骤:
画轴——画底面——画侧棱——连线成图——遮挡的改为虚线
1、水平放置平面图形直观图斜二测画法
小结
x不变,y折半。平行关系不改变
3.多边形原图的面积与其直观图的面积之间的关系为:
【练习1】利用斜二测画法画出边长为3 cm的正方形的直观图,正确的是( )
C
B
A
C
D
【练习2】如图,平行四边形O'P'Q'R'是四边形OPQR的直观图,若O'P'=3,O'R'=1,则原四边形OPQR的周长为 .
10
达标检测
【练习3】
(1)已知等边三角形的边长为4,则用斜二测画法画出的水平放置的直观图
的面积为______.
(2)一个平面图形用斜二测画法画出的水平放置的直观图是边长为1的正方
形,则这个平面图形的面积为______.
x
y
O
C
A
B
x'
y'
O'
C'
A'
B'
x'
y'
O'
C'
A'
B'
x
y
O
C
A
B
用斜二测画法画一个棱长为3cm的正方体的直观图.
D
y
x
O
z
B
C
A'
B'
C'
D'
A
B
C
A'
B'
C'
D'
A
D
教材111页
教材111页
A
D
B
C
F
E
A'
D'
B'
C'
F'
E'
用斜二测画法画一个正六棱柱的直观图.
x'
y'
O'
z'
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
教材111页
一个简单组合体由上下两部分组成,下部是一个圆柱,上部是一个半球,并且半球的球心就是圆柱的上底面圆心. 画出这个组合体的直观图.
O
O′
正五棱锥的直观图的画法:
x'
y'
O'
z'
A
B
C
D
E
S
z'
y'
x'
O'
正三棱柱的直观图的画法:
8.2 立体图形的直观图
人教A版2019高中数学必修第二册
第八章 立体几何初步
请你说出下面几何体分别是什么几何体?
长方体
五棱锥
圆柱
圆锥
圆台
四棱台
这些图形就是空间几何体的直观图
直观图是观察者站在某一点观察一个空间几何体获得的图形。
画立体图形的直观图,实际上是把不完全在同一平面内的点的集合,用同一平面内的点表示。
因此,直观图往往与立体图形的真实形状不完全相同,在立体几何中,立体图形的直观图通常是在平行投影下得到的平面图形。
要画立体图形的直观图,首先要学会画水平放置的平面图形。
观察:如图,矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状?
利用平行投影,人们获得了画直观图的斜二测画法.
下面我们来学习利用这种画法画水平放置的平面图形的直观图.
都是平行四边形
A
B
C
D
y
x
O
y′
x′
O′
D′
C′
B′
A′
用斜二测画法画水平放置的平面图形的直观图的步骤
x不变,y折半
x′
y′
O′
x
y
O
D
A
C
B
D’
A’
C’
B’
M
N
M’
N’
用斜二测画法画水平放置的正方形的直观图
如何在已知图形中建立直角坐标系
①在已知图形中建立直角坐标系时要尽量利用原有图形中的对称性和垂直关系;
②尽可能将关键点放到坐标轴上或是平行于坐标轴的直线上,或是过这些点作平行于坐标轴的直线.
在利用斜二测画法画直观图的过程中,x轴和y轴起到了什么作用
为确定图形中的点的位置提供参照系.
例1、用斜二测画法画水平放置的正六边形的直观图
解:(1)在正六边形ABCDEF中,取AD所在的直线为x轴,对称轴MN所在直线为y轴,两轴交于点O。
画相应的x′轴和y′轴,两轴相交于点O′,使∠x′O′y′=45°
(2)以O'为中心,在x'轴上取A'D' =AD,在y'轴上取
以点N'为中心,画B'C'平行于x'轴,并且等于BC;
再以M'为中心,画E'F'平行于x'轴,并且等于EF。
(3)连接A'B',C'D',E'F',F'A',并擦去辅助线x'轴和y'轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 。
①斜二测画法中,“斜”是指把直角坐标系xOy变为斜坐标系x'O'y',使∠x'O'y'=45 (或135 ),“二测”是指画直观图时,平行于x轴的线段长度不变,平行于y轴的线段长度减半.
②画平面图形的直观图,首先画与坐标轴平行的线段(平行性不变),对于与坐标轴不平行的线段,通过与坐标轴平行的线段确定它的两个端点,然后连接成线段.
斜二测画法画平面图形的直观图的剖析
③斜二测画法的位置特征与度量特征简记为:
x不变,y折半。
平行关系不改变
【练习1】用斜二测画法画水平放置的平面图形的直观图时,下列结论
是否正确?正确的在括号内画“√”,错误的画“×”.
(1)相等的线段在直观图中仍然相等. ( )
(2)平行的线段在直观图中仍然平行. ( )
(3)一个角的直观图仍是一个角. ( )
(4)相等的角在直观图中仍然相等. ( )
√
√
×
×
A
B
C
D
直观图
A′
B′
C′
D′
教材109页
【练习2】用斜二测画法画出水平放置的正三角形的直观图(尺寸自定)
y
x
O
A
B
C
y′
x′
O′
A′
B′
C′
思考 正三角形原图形与直观图的面积具有怎样的数量关系?
结论:
【练习】如图,已知ABC的直观图为A'B'C',若A'C'=A'B'=3,则ABC的面积为___________.
y′
x′
O′
C′
B′
(A′)
9
生活经验告诉我们,水平放置的圆看起来非常像椭圆,立体几何中,我们常用正等测画法画水平放置的圆,在实际画水平放置的圆的直观图时常用下图所示的椭圆模板。
水平放置的圆给我们的视觉效果是什么图形呢?
画几何体的直观图时,一般先使用平面图形的斜二测画法画几何体的底面,这时与画平面图形的直观图相比,只要多画了一个与x轴、y轴都垂直的z轴,并且使平行于z轴的线段的平行性和长度都不变.
下面介绍几种简单几何体的直观图的画法.
x
y
o
z
x
y
o
【例2】已知长方体ABCD-A′B′C′D′的长、宽、高分别为3cm、2cm、1.5cm,
用斜二测画法画出它的直观图.
A
B
C
D
z
[画法]
(1)画轴.
如图,画x轴、y轴、z 轴,三轴相交于点 O(A),使∠xOy=45°,∠xOz=90°.
(2)画底面.
在x轴正半轴上取线段 AB,使AB=3 cm;在y轴正半轴上取线段 AD,使AD=1 cm.
过点B作y轴的平行线,过点D作x轴的平行线,设它们的交点为C,
则□ABCD就是长方体的底面ABCD的直观图.
x
y
o
【例2】已知长方体的长、宽、高ABCD-A′B′C′D′分别为3cm、2cm、1.5cm,
用斜二测画法画出它的直观图.
A
B
C
D
z
A′
B′
C′
D′
A′
B′
C′
D′
A
B
C
D
(3)画侧棱. 在z轴正半轴上取线段AA',使AA'=1.5 cm,过B,C,D各点分别作z 轴平行线,在这些平行线上分别截取1.5 cm长的线段 BB',CC',DD'.
(4)成图.顺次连接A′,B',C',D',并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图了.
练习 棱柱的画法:请画出底面边长为1,高为3的正六棱柱的直观图.
x'
y'
O'
z'
B'
C'
D'
E'
F'
A'
B
C
D
E
F
A
H'
G'
b
a
A
B
C
D
E
F
O
(1)在已知空间几何体中取水平平面,在水平平面内取互相垂直的x轴和y轴,两轴相交于点O.过点O取与x轴、y轴都垂直的z轴. 画直观图时,把它们画成对应的x'轴、y'轴和z'轴,三轴相交于点O',且使∠x'O'y'=45 (或135 ),∠x'O'z'=90 ,x'轴与y'轴所确定的平面表示水平面.
(3)已知几何体中平行于x轴或z轴的线段,在直观图中保持原长度不变,平行于y轴的线段,在直观图中长度为原来的一半.
(2)已知几何体中平行于x轴、y轴或z轴的线段,在直观图中分别画成平行于x'轴、y'轴或z'轴的线段.
4.斜二测画法画空间几何体的直观图的步骤
(4)连线成图以后,擦掉作为辅助线的坐标轴,将被遮挡的部分改为虚线,就得到了空间几何体的直观图.
①画空间几何体的直观图在要求不太严格的情况下,长度和角度可适当选取.为了增强立体感,被挡住的部分通常用虚线表示.
②斜二测画法保持了原图形的平行性、共线性,保持了平行线段的长度比.
斜二测画法画空间几何体的直观图的剖析
③坐标系的建立要充分利用几何体的对称性,坐标原点一般建在图形的对称中心处,使几何体的顶点尽可能多地落在坐标轴上.
④要先画出底面的直观图,再画出其余各面.
【例3】已知圆柱底面半径为1cm,侧面母线长3cm,画出它的直观图.
解:(1)画轴.如图,画x轴,z轴,使∠xOz=90°.
(2)画下底面. 以O为中点,在x轴上取线段AB,使OA=OB=1cm. 利用椭圆模板画椭圆,使其经过A、B两点. 这个椭圆就是圆柱的下底面.
(3)画上底面. 在Oz上截取O',使OO'=3cm. 过点O'作平行于轴Ox的轴O'x'. 类似下底面的作法作出圆柱的上底面.
(4)成图. 连接AA',BB',整理得到圆柱的直观图.
O
圆锥
O
球
对于圆锥的直观图,一般先画圆锥的底面,再借助于圆锥的轴确定圆锥的顶点,最后画出两侧的两条母线.
画球的直观图,一般需要画出球的轮廓线,它是一个圆.同时还经常画出经过球心的截面圆,它们的直观图是椭圆,用以衬托球的立体性.
O
球
【例4】某简单组合体由上下两部分组成,下部是一个圆柱,上部是一个圆锥,圆锥的底面与圆柱的上底面重合.画出这个组合体的直观图.
解:画法:如图,先画出圆柱的上下底面,再在圆柱和圆锥共同的轴线上确定圆锥的顶点,最后画出圆柱和圆锥的母线,并标注相关字母,就得到组合体的直观图.
2、空间几何体直观图斜二测画法步骤:
画轴——画底面——画侧棱——连线成图——遮挡的改为虚线
1、水平放置平面图形直观图斜二测画法
小结
x不变,y折半。平行关系不改变
3.多边形原图的面积与其直观图的面积之间的关系为:
【练习1】利用斜二测画法画出边长为3 cm的正方形的直观图,正确的是( )
C
B
A
C
D
【练习2】如图,平行四边形O'P'Q'R'是四边形OPQR的直观图,若O'P'=3,O'R'=1,则原四边形OPQR的周长为 .
10
达标检测
【练习3】
(1)已知等边三角形的边长为4,则用斜二测画法画出的水平放置的直观图
的面积为______.
(2)一个平面图形用斜二测画法画出的水平放置的直观图是边长为1的正方
形,则这个平面图形的面积为______.
x
y
O
C
A
B
x'
y'
O'
C'
A'
B'
x'
y'
O'
C'
A'
B'
x
y
O
C
A
B
用斜二测画法画一个棱长为3cm的正方体的直观图.
D
y
x
O
z
B
C
A'
B'
C'
D'
A
B
C
A'
B'
C'
D'
A
D
教材111页
教材111页
A
D
B
C
F
E
A'
D'
B'
C'
F'
E'
用斜二测画法画一个正六棱柱的直观图.
x'
y'
O'
z'
A
B
C
D
E
F
A'
B'
C'
D'
E'
F'
教材111页
一个简单组合体由上下两部分组成,下部是一个圆柱,上部是一个半球,并且半球的球心就是圆柱的上底面圆心. 画出这个组合体的直观图.
O
O′
正五棱锥的直观图的画法:
x'
y'
O'
z'
A
B
C
D
E
S
z'
y'
x'
O'
正三棱柱的直观图的画法:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
