8.5.1直线与直线平行课件——2021-2022学年高一下学期数学人教A版(2019)必修第二册(共20张PPT)
文档属性
| 名称 | 8.5.1直线与直线平行课件——2021-2022学年高一下学期数学人教A版(2019)必修第二册(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 588.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 09:30:05 | ||
图片预览


文档简介
(共20张PPT)
8.5.1 直线与直线平行
人教A版2019高中数学必修第二册
8.5 空间直线、平面的平行
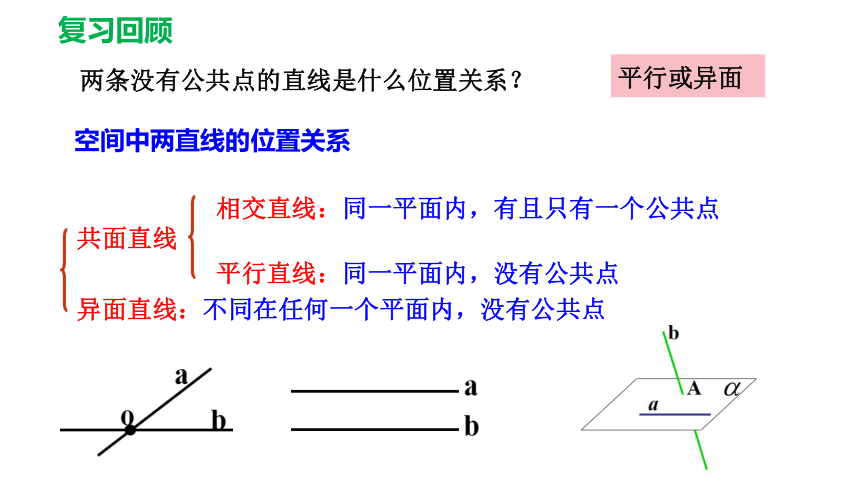
空间中两直线的位置关系
相交直线:同一平面内,有且只有一个公共点
共面直线
平行直线:同一平面内,没有公共点
异面直线:不同在任何一个平面内,没有公共点
两条没有公共点的直线是什么位置关系?
复习回顾
平行或异面
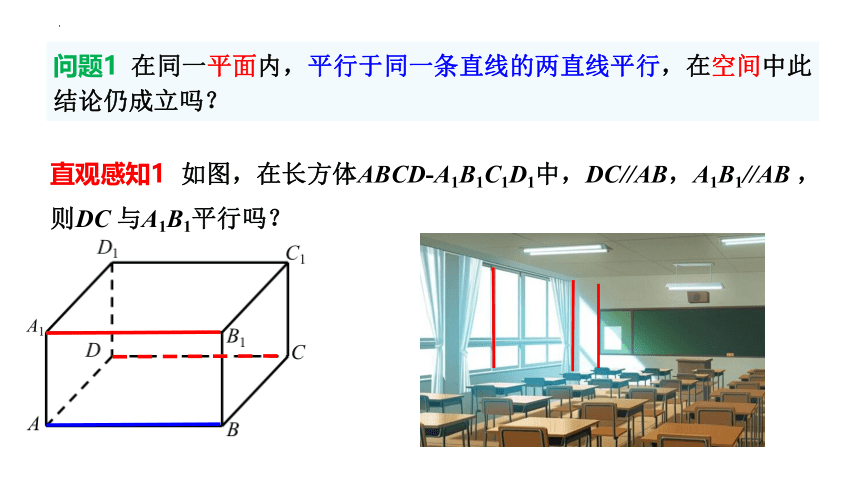
问题1 在同一平面内,平行于同一条直线的两直线平行,在空间中此结论仍成立吗?
直观感知1 如图,在长方体ABCD-A1B1C1D1中,DC//AB,A1B1//AB ,则DC 与A1B1平行吗?
基本事实4的作用:它是判断空间两条直线平行的依据
推广:在空间中平行于一条已知直线的所有直线都互相平行
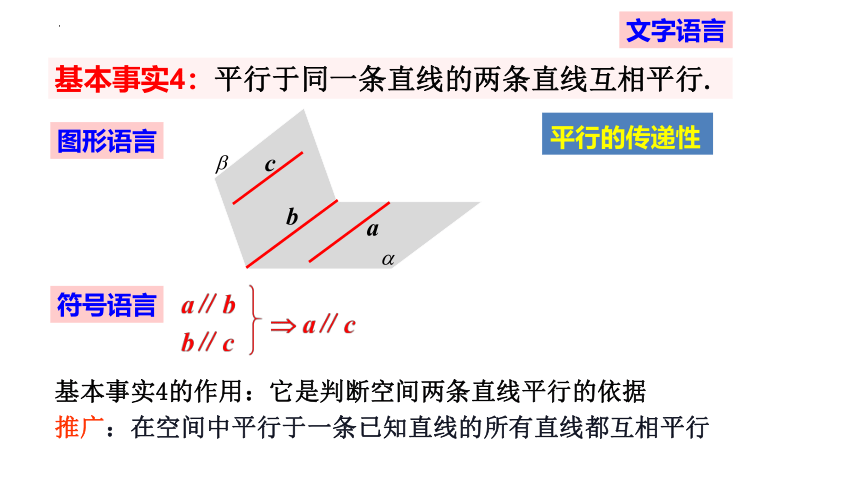
基本事实4:平行于同一条直线的两条直线互相平行.
a
c
b
平行的传递性
符号语言
图形语言
文字语言
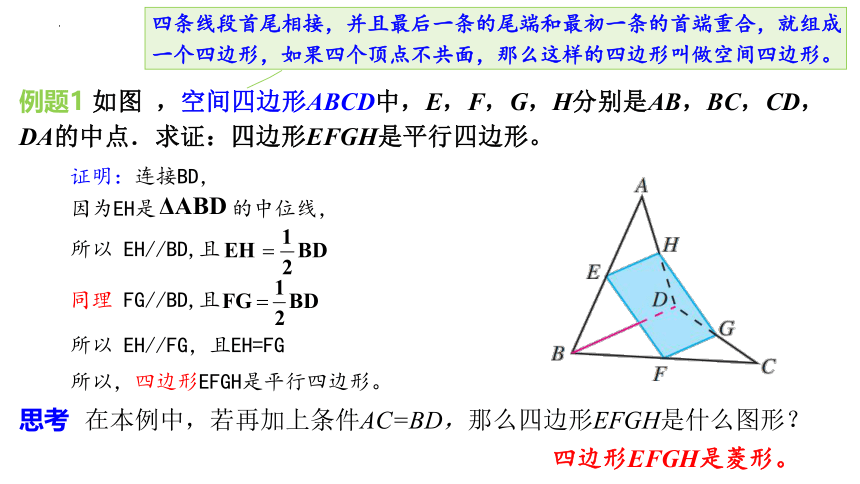
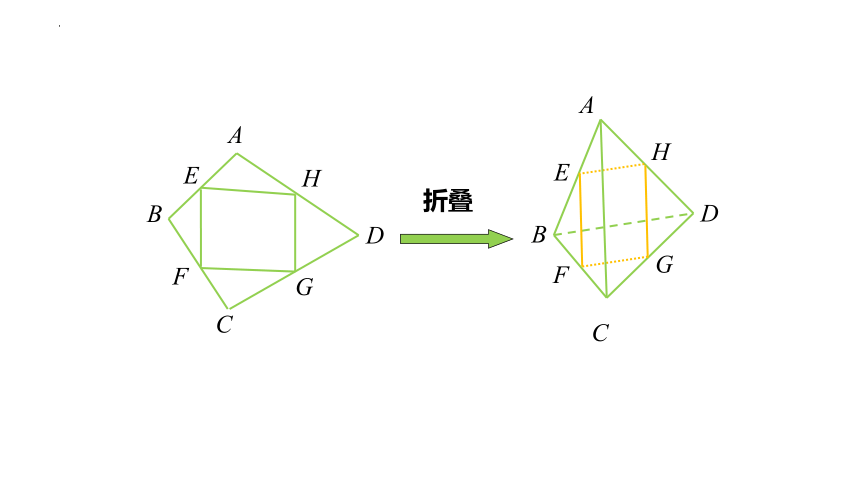
例题1 如图 ,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形。
证明:连接BD,
因为EH是 的中位线,
所以 EH//BD,且
同理 FG//BD,且
所以 EH//FG,且EH=FG
所以,四边形EFGH是平行四边形。
四条线段首尾相接,并且最后一条的尾端和最初一条的首端重合,就组成一个四边形,如果四个顶点不共面,那么这样的四边形叫做空间四边形。
思考 在本例中,若再加上条件AC=BD,那么四边形EFGH是什么图形?
四边形EFGH是菱形。
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
折叠
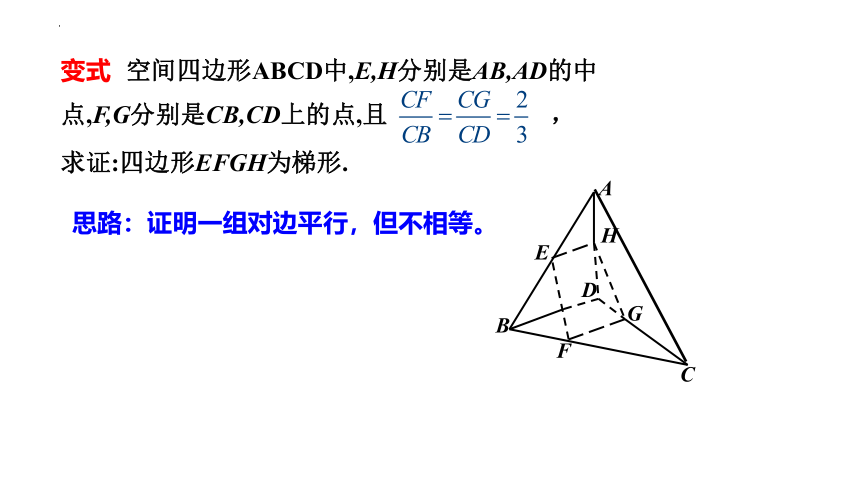
变式 空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且 ,
求证:四边形EFGH为梯形.
A
B
C
D
E
H
F
G
思路:证明一组对边平行,但不相等。
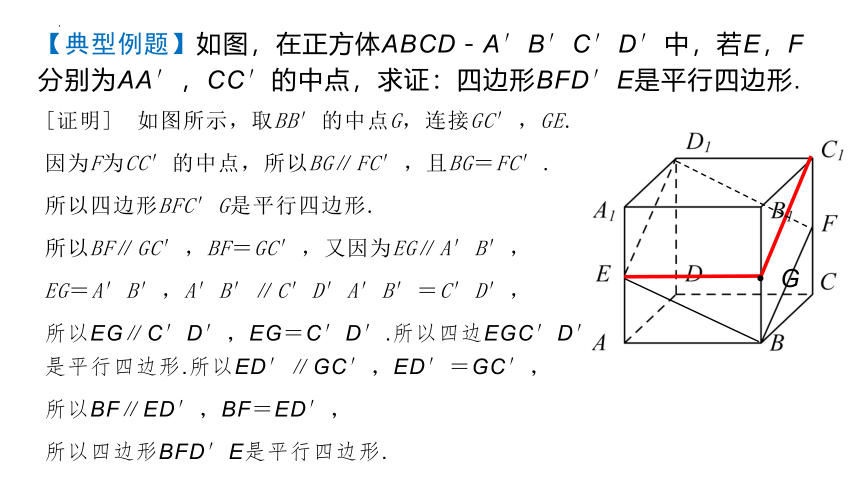
【典型例题】如图,在正方体ABCD-A′B′C′D′中,若E,F分别为AA′,CC′的中点,求证:四边形BFD′E是平行四边形.
[证明] 如图所示,取BB′的中点G,连接GC′,GE.
因为F为CC′的中点,所以BG∥FC′,且BG=FC′.
所以四边形BFC′G是平行四边形.
所以BF∥GC′,BF=GC′,又因为EG∥A′B′,
EG=A′B′,A′B′∥C′D′A′B′=C′D′,
所以EG∥C′D′,EG=C′D′.所以四边EGC′D′是平行四边形.所以ED′∥GC′,ED′=GC′,
所以BF∥ED′,BF=ED′,
所以四边形BFD′E是平行四边形.
G
【归纳】证明空间两直线平行的方法:
(1)基本事实4
用基本事实4证明两条直线平行,只需找到直线b,使得a∥b,同时b∥c,由基本事实4即可得到a∥c.
(2)平面几何法
三角形与梯形中位线、平行四边形的性质、平行线分线段成比例定理等.
(3)定义法
用定义证明两条直线平行,要证明两个方面:一是两条直线在同一平面内;二是两条直线没有公共点(反正法).
空间问题转化为平面问题
问题2 在平面内, 如果一个角的两边与另一个角的两边分别对应平行,这两个角什么关系?
空间中这一结论是否仍然成立呢?
相等或互补
活动1:在桌面上摆出一个角的两边与另一个角的两边分别对应平行,观察这两个角的大小关系(工具:4支笔)
活动2:如果将活动3的角拿到空间中,这两个角是否仍有这样的
大小关系呢?
等角定理:空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补.
一般借助图形判断两个角是相等,还是互补.
(1)
(2)
推论:如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
∴四边形 是平行四边形.
∵ ,∴四边形 是平行四边形.
∴ .
求证:在空间中,如果两个角的两条边分别对应平行,则这两个角相等或互补
∴ .
情形一:分别在∠BAC和∠B A C 的两边上截取AD,AE和
, ,使得AD= ,AE= .连接 , ,
,DE, .
∴DE= .
∴△ADE≌△ .
∴∠BAC=∠ .
显然,当A'C’'的方向与上述情形相反时,这时候∠BAC与∠B'A'C'互补.
情形二:
C’
(1)如果一个角的两边与另一个角的两边平行,那么这两个角相等.( )
(2)如果两个角相等,则它们的边互相平行.( )
练习 1.判断正误
×
×
2.已知,若,则______________.
练习3.如图所示,在正方体ABCD-A1B1C1D1中,E,E1分别是棱AD,A1D1的中点.求证:∠BEC=∠B1E1C1.
证明 如图,连接EE1.
∵E1,E分别为A1D1,AD的中点,∴A1E1∥AE,且A1E1=AE
∴四边形A1E1EA为平行四边形,∴A1A∥E1E,A1A=E1E
又A1A∥B1B,且A1A=B1B∴E1E∥B1B,且E1E=B1B
∴四边形E1EBB1是平行四边形.
∴E1B1∥EB.同理E1C1∥EC.
又∠B1E1C1与∠BEC的两边分别对应平行,由图可知
∴∠B1E1C1=∠BEC.
跟踪训练2 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G分别是AB,BB1,BC的中点,求证:△EFG∽△C1DA1.
证明 如图所示,连接B1C.
因为G,F分别为BC,BB1的中点,
所以GF∥B1C.
又ABCD-A1B1C1D1为正方体,
所以CD∥AB,A1B1∥AB,
由基本事实4知CD∥A1B1,
所以四边形A1B1CD为平行四边形,所以A1D∥B1C.
又B1C∥FG,由基本事实4知A1D∥FG.
同理可证A1C1∥EG,DC1∥EF.
又∠DA1C1与∠EGF,∠A1DC1与∠EFG,∠DC1A1与∠GEF的两条边分别对应平行且均为锐角,
所以∠DA1C1=∠EGF,∠A1DC1=∠EFG,∠DC1A1=∠GEF.
所以△EFG∽△C1DA1.
等角定理:空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补.
基本事实4:平行于同一条直线的两条直线互相平行.
课堂小结
并非所有关于平面的结论都可以推广到空间。
练习 把下列在平面内成立的结论类比地推广到空间,仍然正确的是( )
A. 如果一条直线与两条平行线中的一条相交,则必与另一条相交
B. 如果一条直线与两条平行线中的一条平行,则必与另一条平行
C. 如果两条直线与第三条直线都不相交,则这两条直线不相交
D. 如果两条直线同时与第三条直线垂直,则这两条直线平行
并非所有关于平面的结论都可以推广到空间;
一般来说,要把平面图形的结论推广到立体图形,
必须经过证明.
B
8.5.1 直线与直线平行
人教A版2019高中数学必修第二册
8.5 空间直线、平面的平行
空间中两直线的位置关系
相交直线:同一平面内,有且只有一个公共点
共面直线
平行直线:同一平面内,没有公共点
异面直线:不同在任何一个平面内,没有公共点
两条没有公共点的直线是什么位置关系?
复习回顾
平行或异面
问题1 在同一平面内,平行于同一条直线的两直线平行,在空间中此结论仍成立吗?
直观感知1 如图,在长方体ABCD-A1B1C1D1中,DC//AB,A1B1//AB ,则DC 与A1B1平行吗?
基本事实4的作用:它是判断空间两条直线平行的依据
推广:在空间中平行于一条已知直线的所有直线都互相平行
基本事实4:平行于同一条直线的两条直线互相平行.
a
c
b
平行的传递性
符号语言
图形语言
文字语言
例题1 如图 ,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形。
证明:连接BD,
因为EH是 的中位线,
所以 EH//BD,且
同理 FG//BD,且
所以 EH//FG,且EH=FG
所以,四边形EFGH是平行四边形。
四条线段首尾相接,并且最后一条的尾端和最初一条的首端重合,就组成一个四边形,如果四个顶点不共面,那么这样的四边形叫做空间四边形。
思考 在本例中,若再加上条件AC=BD,那么四边形EFGH是什么图形?
四边形EFGH是菱形。
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
折叠
变式 空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且 ,
求证:四边形EFGH为梯形.
A
B
C
D
E
H
F
G
思路:证明一组对边平行,但不相等。
【典型例题】如图,在正方体ABCD-A′B′C′D′中,若E,F分别为AA′,CC′的中点,求证:四边形BFD′E是平行四边形.
[证明] 如图所示,取BB′的中点G,连接GC′,GE.
因为F为CC′的中点,所以BG∥FC′,且BG=FC′.
所以四边形BFC′G是平行四边形.
所以BF∥GC′,BF=GC′,又因为EG∥A′B′,
EG=A′B′,A′B′∥C′D′A′B′=C′D′,
所以EG∥C′D′,EG=C′D′.所以四边EGC′D′是平行四边形.所以ED′∥GC′,ED′=GC′,
所以BF∥ED′,BF=ED′,
所以四边形BFD′E是平行四边形.
G
【归纳】证明空间两直线平行的方法:
(1)基本事实4
用基本事实4证明两条直线平行,只需找到直线b,使得a∥b,同时b∥c,由基本事实4即可得到a∥c.
(2)平面几何法
三角形与梯形中位线、平行四边形的性质、平行线分线段成比例定理等.
(3)定义法
用定义证明两条直线平行,要证明两个方面:一是两条直线在同一平面内;二是两条直线没有公共点(反正法).
空间问题转化为平面问题
问题2 在平面内, 如果一个角的两边与另一个角的两边分别对应平行,这两个角什么关系?
空间中这一结论是否仍然成立呢?
相等或互补
活动1:在桌面上摆出一个角的两边与另一个角的两边分别对应平行,观察这两个角的大小关系(工具:4支笔)
活动2:如果将活动3的角拿到空间中,这两个角是否仍有这样的
大小关系呢?
等角定理:空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补.
一般借助图形判断两个角是相等,还是互补.
(1)
(2)
推论:如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
∴四边形 是平行四边形.
∵ ,∴四边形 是平行四边形.
∴ .
求证:在空间中,如果两个角的两条边分别对应平行,则这两个角相等或互补
∴ .
情形一:分别在∠BAC和∠B A C 的两边上截取AD,AE和
, ,使得AD= ,AE= .连接 , ,
,DE, .
∴DE= .
∴△ADE≌△ .
∴∠BAC=∠ .
显然,当A'C’'的方向与上述情形相反时,这时候∠BAC与∠B'A'C'互补.
情形二:
C’
(1)如果一个角的两边与另一个角的两边平行,那么这两个角相等.( )
(2)如果两个角相等,则它们的边互相平行.( )
练习 1.判断正误
×
×
2.已知,若,则______________.
练习3.如图所示,在正方体ABCD-A1B1C1D1中,E,E1分别是棱AD,A1D1的中点.求证:∠BEC=∠B1E1C1.
证明 如图,连接EE1.
∵E1,E分别为A1D1,AD的中点,∴A1E1∥AE,且A1E1=AE
∴四边形A1E1EA为平行四边形,∴A1A∥E1E,A1A=E1E
又A1A∥B1B,且A1A=B1B∴E1E∥B1B,且E1E=B1B
∴四边形E1EBB1是平行四边形.
∴E1B1∥EB.同理E1C1∥EC.
又∠B1E1C1与∠BEC的两边分别对应平行,由图可知
∴∠B1E1C1=∠BEC.
跟踪训练2 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G分别是AB,BB1,BC的中点,求证:△EFG∽△C1DA1.
证明 如图所示,连接B1C.
因为G,F分别为BC,BB1的中点,
所以GF∥B1C.
又ABCD-A1B1C1D1为正方体,
所以CD∥AB,A1B1∥AB,
由基本事实4知CD∥A1B1,
所以四边形A1B1CD为平行四边形,所以A1D∥B1C.
又B1C∥FG,由基本事实4知A1D∥FG.
同理可证A1C1∥EG,DC1∥EF.
又∠DA1C1与∠EGF,∠A1DC1与∠EFG,∠DC1A1与∠GEF的两条边分别对应平行且均为锐角,
所以∠DA1C1=∠EGF,∠A1DC1=∠EFG,∠DC1A1=∠GEF.
所以△EFG∽△C1DA1.
等角定理:空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补.
基本事实4:平行于同一条直线的两条直线互相平行.
课堂小结
并非所有关于平面的结论都可以推广到空间。
练习 把下列在平面内成立的结论类比地推广到空间,仍然正确的是( )
A. 如果一条直线与两条平行线中的一条相交,则必与另一条相交
B. 如果一条直线与两条平行线中的一条平行,则必与另一条平行
C. 如果两条直线与第三条直线都不相交,则这两条直线不相交
D. 如果两条直线同时与第三条直线垂直,则这两条直线平行
并非所有关于平面的结论都可以推广到空间;
一般来说,要把平面图形的结论推广到立体图形,
必须经过证明.
B
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
