1.5函数y=Asin(ωx+φ)的图象(上)
文档属性
| 名称 | 1.5函数y=Asin(ωx+φ)的图象(上) |  | |
| 格式 | zip | ||
| 文件大小 | 323.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-03 12:18:38 | ||
图片预览






文档简介
课件28张PPT。函数y=Asin(ωx+φ)的图象(上)湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
教学目的:
1、理解振幅变换和周期变换和平移变换;会用图象变换的方法画y=Asin(ωx+ )的图象 ;
2、会用“五点法”画y=Asin(ωx+ )的图象 ;
3、会求一些函数的振幅、周期、最值等 ;
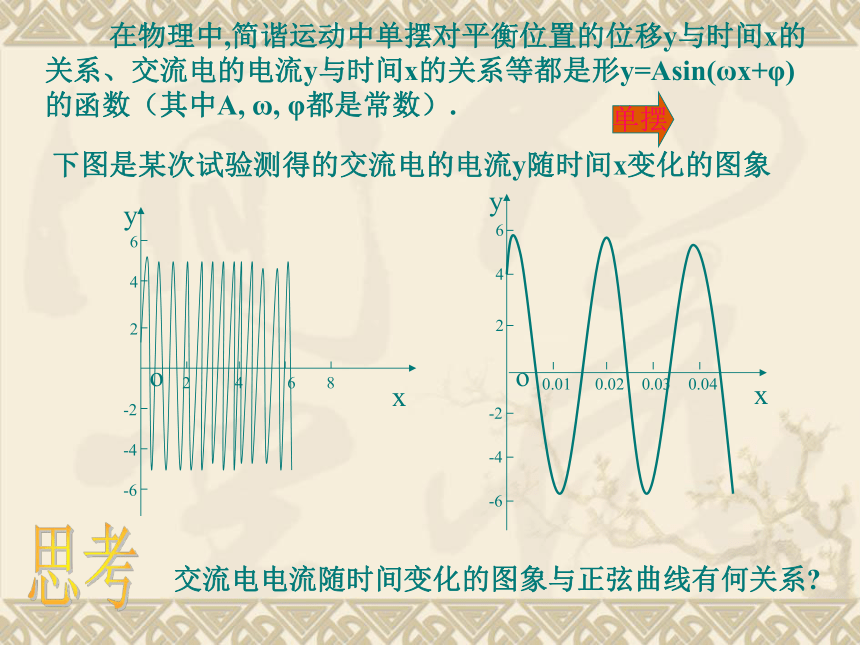
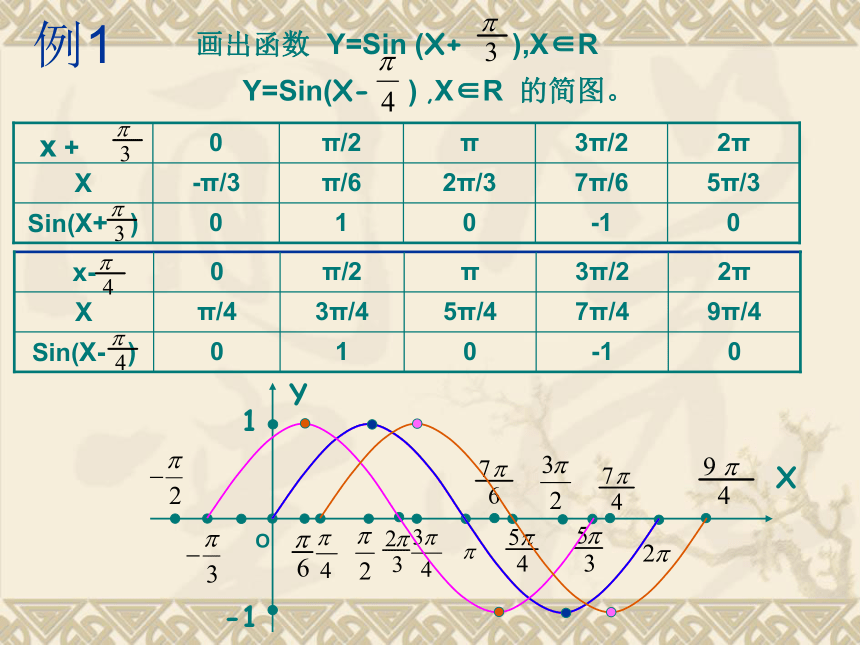
4、渗透分类讨论的数学思想,提高分析和解决问题的能力 。教学重点、难点:难点:理解振幅变换和周期变换和平移变换 。 重点:用图象变换的方法画y=Asin(ωx+ )的图象 。 在物理中,简谐运动中单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形y=Asin(ωx+φ) 的函数(其中A, ω, φ都是常数).下图是某次试验测得的交流电的电流y随时间x变化的图象单摆思考 交流电电流随时间变化的图象与正弦曲线有何关系?例1画出函数 Y=Sin (X+ ),X∈R
Y=Sin(X- ) ,X∈R 的简图。-π/35π/37π/62π/3π/6π/4
9π/47π/45π/43π/4
一般地,函数Y=Sin(X+ψ),X∈R (其中ψ≠0)的
图象,可以看作正弦曲线上所有点向左(当ψ>0时)或向右
(当ψ<0时) 平行移动│ψ│个单位长度而得到。
这种变换称为平移变换。Y=SinXY=Sin(X+ψ), 左移(ψ>0)或
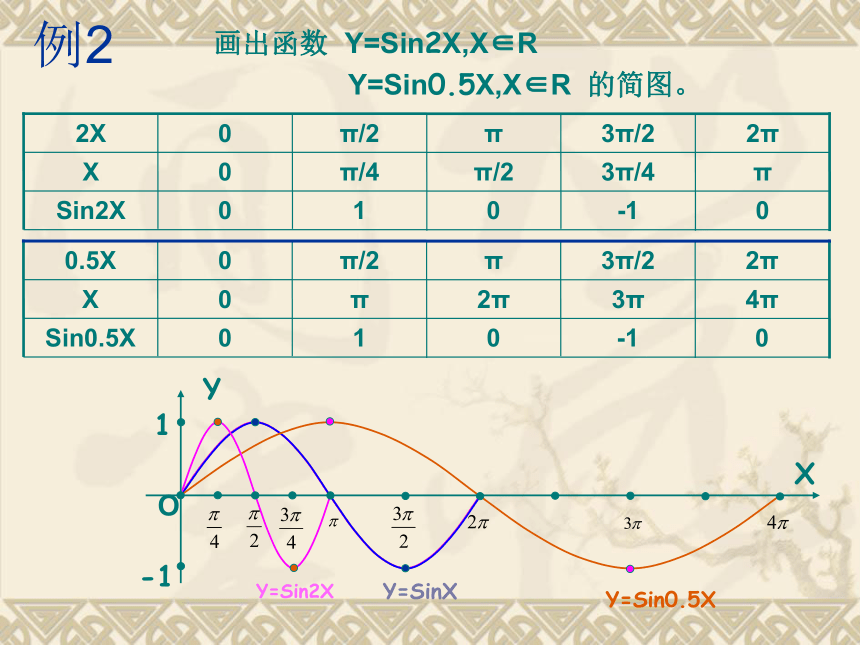
右移(ψ<0) │ψ│ 例2画出函数 Y=Sin2X,X∈R
Y=Sin0.5X,X∈R 的简图。π
3π/4π/2π/40Y=SinXY=Sin2XY=Sin0.5X 纵坐标不变
横坐标变为原来的1/ω倍 一般地,函数Y=SinωX,X∈R (其中ω>0,
且ω≠1)的图象,可以看作正弦曲线上所有点的横坐标
缩短(当ω>1时)或伸长(当0<ω<1时) 到原来的1/ω倍(纵坐标
不变)而得到。
这种变换称为周期变换。Y=SinXY=SinωX例3画出函数 Y=2 SinX,X∈R
Y=0.5 SinX,X∈R 的简图。2π0.5Sin X2Sin XSin X3π/2ππ/20x这两个函数的
周期都是2π ,
我们先画出它们
在[0, 2π]上的简图。思考:
函数Y=2 SinX,X∈R
Y=0.5 SinX,X∈R
的值域是什么? 一般地,函数Y=ASinX,X∈R (其中A>0,
且A≠1)的图象,可以看作正弦曲线上所有点的纵坐标
伸长(当A>1时)或缩短(当0不变)而得到。这种变换叫做振幅变换,A叫做函数
Y=ASinX的振幅。
函数Y=ASinX,X∈R的值域是[-A,A],最大值是A,
最小值是-A。Y=SinXY=ASinX 横坐标不变
纵坐标变为原来的A倍1-12-2xoy3-32??y=Asin(?x+?) (A>0, ?>0) 的图象可由y=sinx经过如下变换得到:y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)?步骤1步骤2步骤3步骤4xyo-11(沿x轴平行移动)(横坐标伸长或缩短)(纵坐标伸长或缩短)解:002-200xy=sinxy=sin2x例2?y=Asin(?x+?) (A>0, ?>0) 的图象可由y=sinx经过如下变换得到:?或:y=sinxy=sin?xy=Asin(?x+?)=sin(?x+?)思考:将函数 的图象变换到函数 (其中A>0, >0)的图象,共有多少种不同的变换次序? 6种!y=sinxy=Asinxy=Asin(x+?)y=Asin(?x+?)y=sinxy=Asinxy=Asin?xy=Asin(?x+?)y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)y=sinxy=sin(x+?)y=Asin(x+?)y=Asin(?x+?)y=sinxy=sin?xy=sin(?x+?)y=Asin(?x+?)y=sinxy=sin?xy=Asin?xy=Asin(?x+?) 解法1: 解法2: 练习归纳小结:1.图象的变换:(1)伸缩变换振幅变换周期变换(2)平移变换上下平移左右平移( ----- 形状变换)( ----- 位置变换)y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)或:y=sinxy=sin?xy=Asin(?x+?)=sin(?x+?)3.函数 (A>0,>0)的图象,可以由函数 的图象通过三次变换而得到,共有6种不同的变换次序.在实际应用中,一般按“左右平移→横向伸缩→纵向伸缩”的次序进行. 作业 4.余弦函数 的图象变换与正弦函数类似,可参照上述原理进行.
高中数学老师欧阳文丰制作
教学目的:
1、理解振幅变换和周期变换和平移变换;会用图象变换的方法画y=Asin(ωx+ )的图象 ;
2、会用“五点法”画y=Asin(ωx+ )的图象 ;
3、会求一些函数的振幅、周期、最值等 ;
4、渗透分类讨论的数学思想,提高分析和解决问题的能力 。教学重点、难点:难点:理解振幅变换和周期变换和平移变换 。 重点:用图象变换的方法画y=Asin(ωx+ )的图象 。 在物理中,简谐运动中单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形y=Asin(ωx+φ) 的函数(其中A, ω, φ都是常数).下图是某次试验测得的交流电的电流y随时间x变化的图象单摆思考 交流电电流随时间变化的图象与正弦曲线有何关系?例1画出函数 Y=Sin (X+ ),X∈R
Y=Sin(X- ) ,X∈R 的简图。-π/35π/37π/62π/3π/6π/4
9π/47π/45π/43π/4
一般地,函数Y=Sin(X+ψ),X∈R (其中ψ≠0)的
图象,可以看作正弦曲线上所有点向左(当ψ>0时)或向右
(当ψ<0时) 平行移动│ψ│个单位长度而得到。
这种变换称为平移变换。Y=SinXY=Sin(X+ψ), 左移(ψ>0)或
右移(ψ<0) │ψ│ 例2画出函数 Y=Sin2X,X∈R
Y=Sin0.5X,X∈R 的简图。π
3π/4π/2π/40Y=SinXY=Sin2XY=Sin0.5X 纵坐标不变
横坐标变为原来的1/ω倍 一般地,函数Y=SinωX,X∈R (其中ω>0,
且ω≠1)的图象,可以看作正弦曲线上所有点的横坐标
缩短(当ω>1时)或伸长(当0<ω<1时) 到原来的1/ω倍(纵坐标
不变)而得到。
这种变换称为周期变换。Y=SinXY=SinωX例3画出函数 Y=2 SinX,X∈R
Y=0.5 SinX,X∈R 的简图。2π0.5Sin X2Sin XSin X3π/2ππ/20x这两个函数的
周期都是2π ,
我们先画出它们
在[0, 2π]上的简图。思考:
函数Y=2 SinX,X∈R
Y=0.5 SinX,X∈R
的值域是什么? 一般地,函数Y=ASinX,X∈R (其中A>0,
且A≠1)的图象,可以看作正弦曲线上所有点的纵坐标
伸长(当A>1时)或缩短(当0
Y=ASinX的振幅。
函数Y=ASinX,X∈R的值域是[-A,A],最大值是A,
最小值是-A。Y=SinXY=ASinX 横坐标不变
纵坐标变为原来的A倍1-12-2xoy3-32??y=Asin(?x+?) (A>0, ?>0) 的图象可由y=sinx经过如下变换得到:y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)?步骤1步骤2步骤3步骤4xyo-11(沿x轴平行移动)(横坐标伸长或缩短)(纵坐标伸长或缩短)解:002-200xy=sinxy=sin2x例2?y=Asin(?x+?) (A>0, ?>0) 的图象可由y=sinx经过如下变换得到:?或:y=sinxy=sin?xy=Asin(?x+?)=sin(?x+?)思考:将函数 的图象变换到函数 (其中A>0, >0)的图象,共有多少种不同的变换次序? 6种!y=sinxy=Asinxy=Asin(x+?)y=Asin(?x+?)y=sinxy=Asinxy=Asin?xy=Asin(?x+?)y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)y=sinxy=sin(x+?)y=Asin(x+?)y=Asin(?x+?)y=sinxy=sin?xy=sin(?x+?)y=Asin(?x+?)y=sinxy=sin?xy=Asin?xy=Asin(?x+?) 解法1: 解法2: 练习归纳小结:1.图象的变换:(1)伸缩变换振幅变换周期变换(2)平移变换上下平移左右平移( ----- 形状变换)( ----- 位置变换)y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)或:y=sinxy=sin?xy=Asin(?x+?)=sin(?x+?)3.函数 (A>0,>0)的图象,可以由函数 的图象通过三次变换而得到,共有6种不同的变换次序.在实际应用中,一般按“左右平移→横向伸缩→纵向伸缩”的次序进行. 作业 4.余弦函数 的图象变换与正弦函数类似,可参照上述原理进行.
