2013学年宁波初三复习会议资料 课堂的自然生成让复习课更高效
文档属性
| 名称 | 2013学年宁波初三复习会议资料 课堂的自然生成让复习课更高效 |  | |
| 格式 | zip | ||
| 文件大小 | 485.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-03 12:43:42 | ||
图片预览




文档简介
课件17张PPT。课堂的自然生成
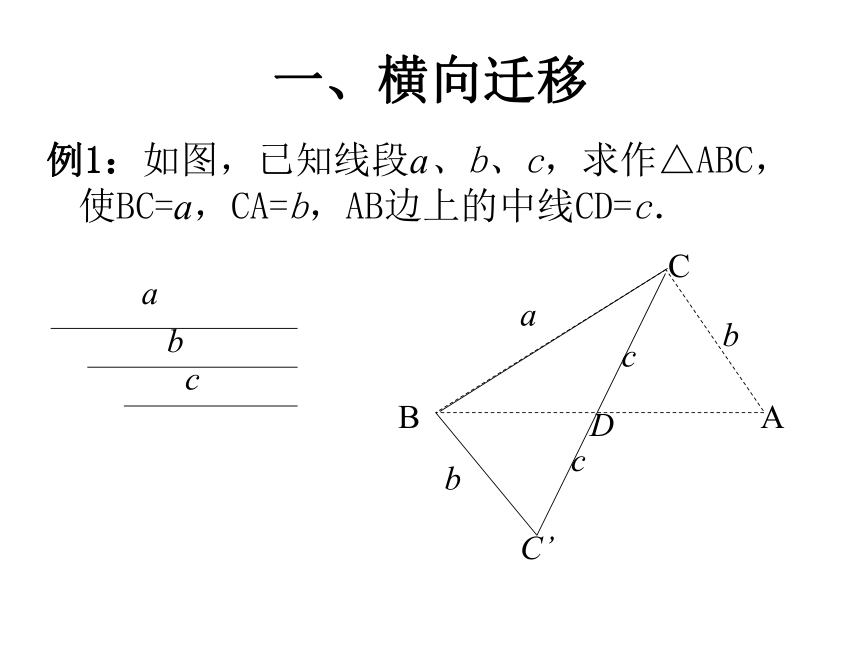
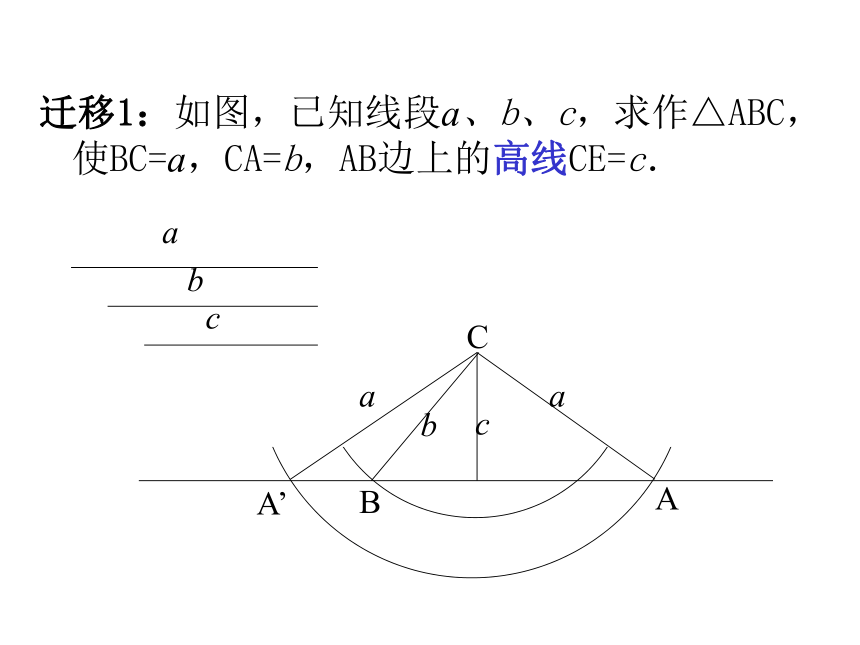
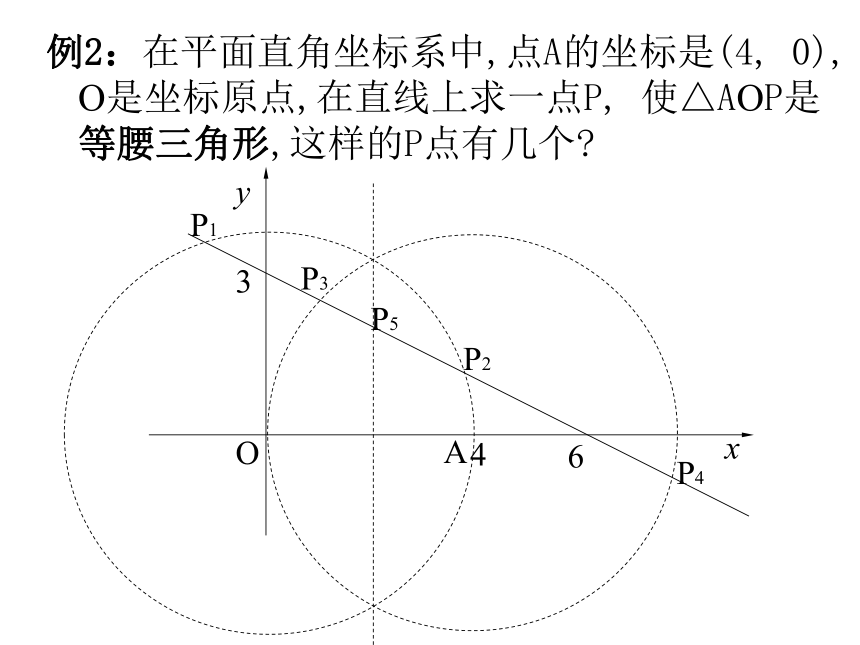
让复习课更高效宁波外国语学校 王波明 纵观近几年中考数学试卷,其特点都是起点低,入手容易,注重基础,知识覆盖面广,注重创造性思维和综合能力的考查.一方面从课本中取材或适当改编,来考查学生的基础知识、基本技能、基本思想方法和基本活动经验,另一方面又出现各类创新题和综合题,要求学生在短时间内汇集有关概念、公式、定理,用各种数学思想方法来探索解题途径. 所以初三复习不应该只是对知识进行简单的重复整理,或是一味地 “多练多考”,而是需要强化知识间的联系沟通,体现系统性。这就要求我们平时在课堂上多关注学生的学习思考过程,注重数学学习的横向迁移,纵向拓展,一题多解,尊重学生的想法,培养拓展创新的能力.一、横向迁移例1:如图,已知线段a、b、c,求作△ABC,使BC=a,CA=b,AB边上的中线CD=c.迁移1:如图,已知线段a、b、c,求作△ABC,使BC=a,CA=b,AB边上的高线CE=c. 迁移2:如图,已知线段a、b、c,求作△ABC,使BC=a,CA=b,∠C的角平分线CF=c. 例2:在平面直角坐标系中,点A的坐标是(4, 0), O是坐标原点,在直线上求一点P, 使△AOP是等腰三角形,这样的P点有几个?迁移1:在平面直角坐标系中,点A的坐标是(4, 0),O是坐标原点,在直线上求一点Q, 使△AOQ是直角三角形,这样的Q点有几个?二、纵向拓展例3:如图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派三名救生员前去营救。1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑到C点.再跳入海中;3号救生员沿岸边向前跑300米到离B点最近的D点,再跳入海中.救生员在岸上跑的速度都是6米/秒,在水中游泳的速度都是2米/秒。若∠BAD=45°,∠BCD=60°,三名救生员同时从A点出发,请说明谁先到达营救地点B.
(参考数据 )我们的疑问:
救生员从A点出发,沿岸边向前跑到E点.再跳入海中,若要最先到达营救地点B.如何确定E点?三、一题多解 我希望自己在课堂上不是单纯对学生进行知识灌输,能尽力做到引导和鼓励学生发现问题,让学生提出自己的各种想法,给他们检验自己见解的机会.让初三的复习课有更多自然生成的东西,使数学学习的过程更快乐、更高效!
(参考数据 )我们的疑问:
救生员从A点出发,沿岸边向前跑到E点.再跳入海中,若要最先到达营救地点B.如何确定E点?三、一题多解 我希望自己在课堂上不是单纯对学生进行知识灌输,能尽力做到引导和鼓励学生发现问题,让学生提出自己的各种想法,给他们检验自己见解的机会.让初三的复习课有更多自然生成的东西,使数学学习的过程更快乐、更高效!
同课章节目录
