2013学年宁波初三复习会议资料 说明解读
文档属性
| 名称 | 2013学年宁波初三复习会议资料 说明解读 |  | |
| 格式 | zip | ||
| 文件大小 | 95.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-03 12:49:52 | ||
图片预览








文档简介
课件24张PPT。——《说明》解读与命题思考心动风才动 浙江宁海桃源中学 王伟
tyzxww@126.com一.考试说明的内容板块:
(1)考试范围和要求;基础知识,基本技 能,数学思考,解决问题
(2)考试形式
(3)考试目标
(4)例卷、答案、评分标准
2.相关附件:
(1)初中数学学业考试典型题目示例
宁波及其他省、市部分值得研究
的中考试题
(2)5份评估练习卷
一线骨干教师或教研员根据自己对新 课程的理解和考试要求命题
1.考试范围、要求、形式(1).考试采用闭卷形式。
满分130分,考试时间120分。
试卷采用卷一、卷二两部分,卷一为选择题卷(采用电脑阅卷的形式),卷二为非选择题卷。
(2).考试内容与分布数与代数:约占42%
空间与图形:约占38%
统计与概率:约占15%
实践与综合运用(课题学习):约占5%
注意:删减有关计算机的内容(3).试题类型分布选择题:共12题,36分
填空题:共6题,18分
解答题:共8题,76分,其中第19题6分,20题7分,21题7分,22题9分,23题9分,24题12分,25题12分,26题14分(4).试题难度分布试题按其难度分为容易题、稍难题、较难题,整卷难度不低于0.70
容易题(难度0.8以上): 约占70%
稍难题(难度0.4~0.8): 约占20%
较难题(难度0.4以下): 约占10%二、《说明》带给我们的命题思考:(一)怎样依据学科特点,编制在简约中蕴含 “数学味”的容易题?
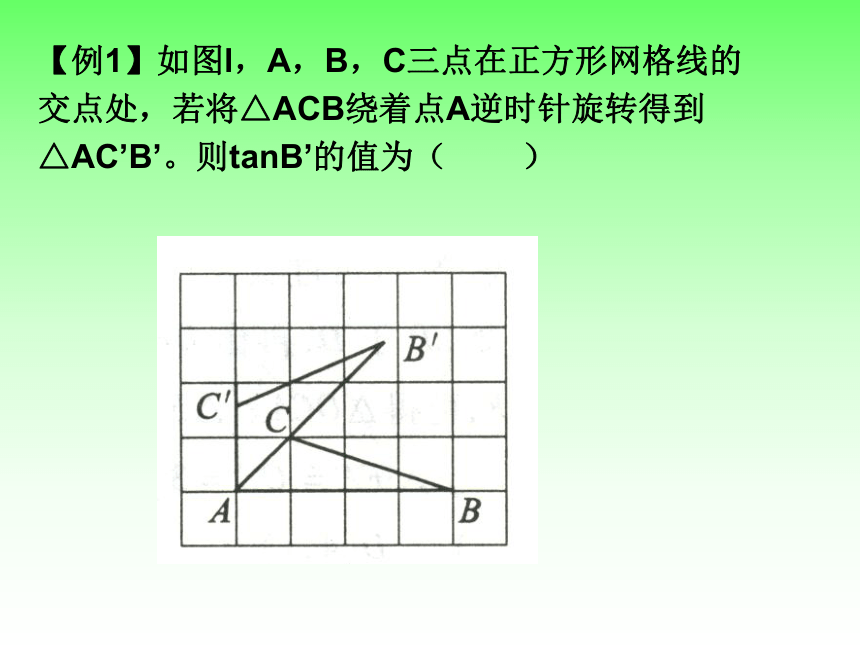
化简: = ▲ . 例卷第14题【例1】如图l,A,B,C三点在正方形网格线的
交点处,若将△ACB绕着点A逆时针旋转得到
△AC’B’。则tanB’的值为( )
(二)怎样立足课本,编制有利于引导 师生认真研究教材、吃透教材的基本题?
20.如图,直线y=2x-6与反比例函数
(x>0)的图象交于A(4,2),与x轴交与点B.
(1)求k的值及点B的坐标;
2)在x轴上是否存在点C,
使得AC=AB?若存在,
求出点?C的坐标;若不存在,
请说明理由。
(评估练习五第20题)25.(本题10分)如图,菱形ABCD中,E,F,G,H分别在AB,BC,CD,DA上,AE=AH=BF=DG=x,设四边形EFGH的面积为S.
(1)求证:△BEF≌△DHG;
(2)已知∠B=600,AB=2.当x变化时,S是变量
还是常量?如果是变量,写出S与x的函数关系式,
如果是常量,请说明理由,并求出S的值;
(3)已知EH=EF=5,FG=11,求tanB的值及AB的长
(例卷25题)
MN(三)怎样将PISA为生存而学习的思想和PISA
能力测试方法渗透到学业考试命题中?【例4】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是
(A)4m cm (B)4n cm (C) 2(m+n) cm (D)4(m-n) cm
(考例 例4)11.易拉罐装的某种饮料一箱24瓶(易拉罐可视作圆柱).小明设计了两种形式的长方体包装箱,如图是箱子底部的摆放形式. ( )
方案1:如图1,底部横行放6瓶,直列放4瓶,共放一层;
方案2:如图2,底部横行放4瓶,直列放3瓶,共放二层;
若易拉罐总体积与纸箱容积的比叫做纸箱空间的利用率,设方案1和方案2的纸箱空间的
利用率分别为,,则
(A) (B) (C)
(D)大小不确定
(例卷11题)命题探究走在了全国前列 (浙江省09年初中毕业生学业考试试卷质量评价报告)数学素养教育理念教学质量命题探究(四)怎样根据新课程理念,编好设计新颖
的特色试题?例1:A市、B市分别有电子计算机10台和4台,现决定把这些计算机支援给C市8台,D市6台,已知:从A市调运一台计算机到C市、D市的运费分别为800元和400元;从B市调运一台计算机到C市、D市的运费分别为500元和300元.
(1)若总运费为8400元,B市运往D市应是多少台?
(2)若要求总运费不超过8200元,共有几种调运方 案?
(3)求出总运费最低的调运方案,最低总运费是多少元? (1997年宁波市中考题)变式 A市、B市和C市分别有某种机器10台、10台和8台.现决定把这些机器支援给D市18台,E市10台,已知:从A市调运一台机器到D市、E市的运费分别为200元和800元;从B市调运一台机器到D市、E市的运费分别为300元和700元;从C市调运一台机器到D市、E市的运费分别为400元和500元.
(1)设从A市、B市各调x台到D市,当28台机器全部调运完毕后,求总运费W元)关于x(台)的函数关系式,并求W的最小值和最大值;
(2)设从A市调x台到D市,B市调y台到D市当28台机器全部调运完毕后,用x,y表示总运费W(元),并求W的最小值和最大值.(1998年全国初中数学竞赛)例2 小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米. 小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在天一阁查阅资料的时间为 ▲ 分钟,小聪返回学校的速度为 ▲ 千米/分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
(2010年宁波市中考题)点评:本题源自浙教版教材的函数应用题,实际背景都是学生所熟悉的,但在编拟的结构和内容中,视角独特。问题设置了“信息读取”,“图象理解”,“问题解决”三个板块。主要考查学生应用一次函数知识分析问题、解决问题的能力,渗透了数形结合、方程、待定系数法等重要的思想和方法.试题文字简洁、通俗易懂,有效地避免了因曲解题意造成的对学生答题的干扰,突出了考查的重点,保证了试题的效度。本题入口宽,方法灵活多样,除可利用一次函数知识外也可利用图形中的条件选择相似三角形知识等多种方法来解决问题。第25题:十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)
之间存在的一个有趣的关系式,被称为欧拉公式. 请你观察下列几种简单多面体模型,解答下列问题:四面体 长方体 正八面体 正十二面体
多面体顶点数(V)面数(F)棱数(E)四面体44▲长方体8612正八面体▲812正十二面体201230根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 ▲ ;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 ▲ ;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱. 设该多面体外表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
(2010年宁波市中考题)
25.(本题10分)阅读下面的情景对话,然后解答问题:老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形
叫做奇异三角形
小明:那直角三角形中是否存在奇异三角形呢?
小明:那直角三角形中是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?(第25题)ABCDEO
(2)在Rt△ABC中,∠ACB=90°,AB=,AC=,BC=,且,若Rt△ABC是奇异三角形,求;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆ADB的中点, C、D在直径AB两侧,若在⊙O内存在点E,使得AE=AD,CB=CE.
① 求证:△ACE是奇异三角形;
② 当△ACE是直角三角形时,求∠AOC的度数.
(2011年宁波市中考题)
三、提出探讨的命题的“浪漫”思考 思考1:命题中如何体现“不同的人在数学上得到不同的发展”24. “6”字形图中,FM是大圆的直径,BC与大圆相切于B,OB与小圆相交于点A,AD∥BC,CD∥BH∥FM,DH⊥BH于H,设∠FOB=α ,BC=6.(第24题图)
(1)求证:AD为小圆的切线;
(2)在图中找出一个可用α表示的角(除∠FOB外),并说明你这样表示的理由;(根据所写结果的正确性及所需推理过程的难易程度得分略有差异)
(3)当α=30o时,求DH的长。(结果保留根号)
(评估练习(四) 第24题)思考2、命题中如何体现“学生质疑—发现和提出问题”在课程标准中,创新意识是此次修改新增加的一个核心概念。标准指出:“创新意识的培养是现代数学教育的基本任务,应体现在数学教与学的过程之中。学生自己发现和提出问题是创新的基础;独立思考、学会思考是创新的核心;归纳概括得到猜想和规律,并加以验证,是创新的重要方法。创新意识的培养应该从义务教育阶段做起,贯穿数学教育的始终。”解决问题问题解决谢谢
大家
tyzxww@126.com一.考试说明的内容板块:
(1)考试范围和要求;基础知识,基本技 能,数学思考,解决问题
(2)考试形式
(3)考试目标
(4)例卷、答案、评分标准
2.相关附件:
(1)初中数学学业考试典型题目示例
宁波及其他省、市部分值得研究
的中考试题
(2)5份评估练习卷
一线骨干教师或教研员根据自己对新 课程的理解和考试要求命题
1.考试范围、要求、形式(1).考试采用闭卷形式。
满分130分,考试时间120分。
试卷采用卷一、卷二两部分,卷一为选择题卷(采用电脑阅卷的形式),卷二为非选择题卷。
(2).考试内容与分布数与代数:约占42%
空间与图形:约占38%
统计与概率:约占15%
实践与综合运用(课题学习):约占5%
注意:删减有关计算机的内容(3).试题类型分布选择题:共12题,36分
填空题:共6题,18分
解答题:共8题,76分,其中第19题6分,20题7分,21题7分,22题9分,23题9分,24题12分,25题12分,26题14分(4).试题难度分布试题按其难度分为容易题、稍难题、较难题,整卷难度不低于0.70
容易题(难度0.8以上): 约占70%
稍难题(难度0.4~0.8): 约占20%
较难题(难度0.4以下): 约占10%二、《说明》带给我们的命题思考:(一)怎样依据学科特点,编制在简约中蕴含 “数学味”的容易题?
化简: = ▲ . 例卷第14题【例1】如图l,A,B,C三点在正方形网格线的
交点处,若将△ACB绕着点A逆时针旋转得到
△AC’B’。则tanB’的值为( )
(二)怎样立足课本,编制有利于引导 师生认真研究教材、吃透教材的基本题?
20.如图,直线y=2x-6与反比例函数
(x>0)的图象交于A(4,2),与x轴交与点B.
(1)求k的值及点B的坐标;
2)在x轴上是否存在点C,
使得AC=AB?若存在,
求出点?C的坐标;若不存在,
请说明理由。
(评估练习五第20题)25.(本题10分)如图,菱形ABCD中,E,F,G,H分别在AB,BC,CD,DA上,AE=AH=BF=DG=x,设四边形EFGH的面积为S.
(1)求证:△BEF≌△DHG;
(2)已知∠B=600,AB=2.当x变化时,S是变量
还是常量?如果是变量,写出S与x的函数关系式,
如果是常量,请说明理由,并求出S的值;
(3)已知EH=EF=5,FG=11,求tanB的值及AB的长
(例卷25题)
MN(三)怎样将PISA为生存而学习的思想和PISA
能力测试方法渗透到学业考试命题中?【例4】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是
(A)4m cm (B)4n cm (C) 2(m+n) cm (D)4(m-n) cm
(考例 例4)11.易拉罐装的某种饮料一箱24瓶(易拉罐可视作圆柱).小明设计了两种形式的长方体包装箱,如图是箱子底部的摆放形式. ( )
方案1:如图1,底部横行放6瓶,直列放4瓶,共放一层;
方案2:如图2,底部横行放4瓶,直列放3瓶,共放二层;
若易拉罐总体积与纸箱容积的比叫做纸箱空间的利用率,设方案1和方案2的纸箱空间的
利用率分别为,,则
(A) (B) (C)
(D)大小不确定
(例卷11题)命题探究走在了全国前列 (浙江省09年初中毕业生学业考试试卷质量评价报告)数学素养教育理念教学质量命题探究(四)怎样根据新课程理念,编好设计新颖
的特色试题?例1:A市、B市分别有电子计算机10台和4台,现决定把这些计算机支援给C市8台,D市6台,已知:从A市调运一台计算机到C市、D市的运费分别为800元和400元;从B市调运一台计算机到C市、D市的运费分别为500元和300元.
(1)若总运费为8400元,B市运往D市应是多少台?
(2)若要求总运费不超过8200元,共有几种调运方 案?
(3)求出总运费最低的调运方案,最低总运费是多少元? (1997年宁波市中考题)变式 A市、B市和C市分别有某种机器10台、10台和8台.现决定把这些机器支援给D市18台,E市10台,已知:从A市调运一台机器到D市、E市的运费分别为200元和800元;从B市调运一台机器到D市、E市的运费分别为300元和700元;从C市调运一台机器到D市、E市的运费分别为400元和500元.
(1)设从A市、B市各调x台到D市,当28台机器全部调运完毕后,求总运费W元)关于x(台)的函数关系式,并求W的最小值和最大值;
(2)设从A市调x台到D市,B市调y台到D市当28台机器全部调运完毕后,用x,y表示总运费W(元),并求W的最小值和最大值.(1998年全国初中数学竞赛)例2 小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米. 小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在天一阁查阅资料的时间为 ▲ 分钟,小聪返回学校的速度为 ▲ 千米/分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
(2010年宁波市中考题)点评:本题源自浙教版教材的函数应用题,实际背景都是学生所熟悉的,但在编拟的结构和内容中,视角独特。问题设置了“信息读取”,“图象理解”,“问题解决”三个板块。主要考查学生应用一次函数知识分析问题、解决问题的能力,渗透了数形结合、方程、待定系数法等重要的思想和方法.试题文字简洁、通俗易懂,有效地避免了因曲解题意造成的对学生答题的干扰,突出了考查的重点,保证了试题的效度。本题入口宽,方法灵活多样,除可利用一次函数知识外也可利用图形中的条件选择相似三角形知识等多种方法来解决问题。第25题:十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)
之间存在的一个有趣的关系式,被称为欧拉公式. 请你观察下列几种简单多面体模型,解答下列问题:四面体 长方体 正八面体 正十二面体
多面体顶点数(V)面数(F)棱数(E)四面体44▲长方体8612正八面体▲812正十二面体201230根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 ▲ ;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 ▲ ;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱. 设该多面体外表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
(2010年宁波市中考题)
25.(本题10分)阅读下面的情景对话,然后解答问题:老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形
叫做奇异三角形
小明:那直角三角形中是否存在奇异三角形呢?
小明:那直角三角形中是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?(第25题)ABCDEO
(2)在Rt△ABC中,∠ACB=90°,AB=,AC=,BC=,且,若Rt△ABC是奇异三角形,求;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆ADB的中点, C、D在直径AB两侧,若在⊙O内存在点E,使得AE=AD,CB=CE.
① 求证:△ACE是奇异三角形;
② 当△ACE是直角三角形时,求∠AOC的度数.
(2011年宁波市中考题)
三、提出探讨的命题的“浪漫”思考 思考1:命题中如何体现“不同的人在数学上得到不同的发展”24. “6”字形图中,FM是大圆的直径,BC与大圆相切于B,OB与小圆相交于点A,AD∥BC,CD∥BH∥FM,DH⊥BH于H,设∠FOB=α ,BC=6.(第24题图)
(1)求证:AD为小圆的切线;
(2)在图中找出一个可用α表示的角(除∠FOB外),并说明你这样表示的理由;(根据所写结果的正确性及所需推理过程的难易程度得分略有差异)
(3)当α=30o时,求DH的长。(结果保留根号)
(评估练习(四) 第24题)思考2、命题中如何体现“学生质疑—发现和提出问题”在课程标准中,创新意识是此次修改新增加的一个核心概念。标准指出:“创新意识的培养是现代数学教育的基本任务,应体现在数学教与学的过程之中。学生自己发现和提出问题是创新的基础;独立思考、学会思考是创新的核心;归纳概括得到猜想和规律,并加以验证,是创新的重要方法。创新意识的培养应该从义务教育阶段做起,贯穿数学教育的始终。”解决问题问题解决谢谢
大家
同课章节目录
